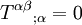Tenseur energie-impulsion

Tenseur energie-impulsion

Tenseur énergie-impulsion

Le tenseur énergie-impulsion est un outil mathématique utilisé notamment en relativité générale afin de représenter la répartition de masse et d'énergie dans l'espace-temps.

La théorie de la relativité restreinte d'Einstein établissant l'équivalence entre masse et énergie, la théorie de la relativité générale indique que ces dernières courbent l'espace. L'effet visible de cette courbure est la déviation de la trajectoire des objets en mouvement, observé couramment comme l'effet de la gravitation.

Sommaire

Tenseur énergie-impulsion

Les composants du tenseur énergie-impulsion.

Le tenseur énergie-impulsion peut s'écrire sous la forme d'une matrice 4x4 réelle symétrique :

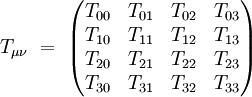
T_{\mu \nu} \ = \ \left( \begin{matrix} T_{00} & T_{01} & T_{02} & T_{03} \\ T_{10} & T_{11} & T_{12} & T_{13} \\ T_{20} & T_{21} & T_{22} & T_{23} \\ T_{30} & T_{31} & T_{32} & T_{33} \end{matrix} \right)

On y retrouve les grandeurs physiques suivantes :

T00 est la densité volumique d'énergie. Elle est positive.
T10, T20, T30 sont les densités de moments.
T01, T02, T03 sont les flux d'énergie.


La sous-matrice 3 x 3 des composantes spatiale-spatiale :
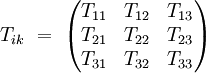
T_{ik} \ = \ \left( \begin{matrix} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{matrix} \right)

est la matrice des flux de moments. En mécanique des fluides, sa diagonale correspond à la pression, et les autres composantes correspondent aux efforts tangentiels dus à la viscosité.

Construction

Pour une théorie décrite par une densité lagrangiennne 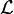\mathcal{L}, l'action s'écrit comme une intégrale sur l'espace-temps :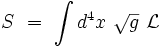

S \ = \ \int d^4x \ \sqrt{g} \ \mathcal{L}

où 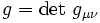g = \mathrm{det} \ g_{\mu \nu} est le déterminant du tenseur métrique de l'espace-temps. Le tenseur énergie-impulsion associé est défini par la variation de l'action par rapport à la métrique inverse :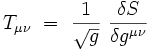

T_{\mu \nu} \ = \ \frac{1}{\sqrt{g}} \ \frac{\delta S}{\delta g^{\mu \nu}}

Exemples

Pour un fluide au repos, le tenseur énergie-impulsion se réduit à la matrice diagonale diag(ρc^2,p,p,p) où ρ est la masse volumique et p la pression hydrostatique.

Propriétés

Le tenseur impulsion-énergie est symétrique :

Tαβ = Tβα

Le tenseur impulsion-énergie est à divergence nulle :

{T^{\alpha \beta}}_{; \alpha} = 0

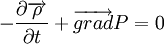Dans le cas d'un fluide parfait, où Tαβ = Pgαβ − (ρ + P)uαuβ, en métrique plate, cette condition de divergence nulle redonne la loi newtonienne bien connue : -\frac {\partial \overrightarrow \rho} {\partial t} + \overrightarrow {grad} P = 0 .

Voir aussi

Bibliographie

  • Portail de la physique Portail de la physique
Ce document provient de « Tenseur %C3%A9nergie-impulsion ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Tenseur energie-impulsion de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Tenseur énergie impulsion — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur énergie-impulsion — Le tenseur énergie impulsion est un outil mathématique utilisé notamment en relativité générale afin de représenter la répartition de masse et d énergie dans l espace temps. La théorie de la relativité restreinte d Einstein établissant l… …   Wikipédia en Français

  • tenseur d’énergie-impulsion — energijos impulso tenzorius statusas T sritis fizika atitikmenys: angl. energy momentum tensor vok. Energie Impuls Tensor, m rus. тензор энергии импульса, m pranc. tenseur d’énergie impulsion, m …   Fizikos terminų žodynas

  • Tenseur de bel-robinson — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur de ricci — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur de levi-civita — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur dualiseur — Tenseur de Levi Civita Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur de courbure — Tenseur de Riemann Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur de killing-yano — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur de riemann — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”