Vecteur tangent

Vecteur tangent

Espace tangent

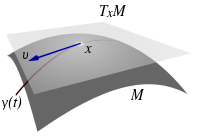
L'espace tangent en un point a d'une variété différentielle M est un espace vectoriel qui intuitivement est l'ensemble de tous les vecteurs-vitesse possibles d'un "mobile" se déplaçant (sans pouvoir la quitter) dans la variété M quand il est en a.

Une façon commune en physique de décrire l'espace tangent est de dire que les vecteurs qu'il contient représentent les différences entre ce point et des points de la variété infiniment proches du premier. Cette façon d'interpréter l'espace tangent revient à considérer que la variété a localement une structure proche de celle d'un espace affine.

Sommaire

Définition lorsque la variété est plongée

Lorsque la variété est plongée dans \mathbb{R}^n, l'espace tangent en un point p est simplement l'ensemble des vecteurs tangents en p aux courbes (de classe C1) tracées sur la variété et contenant p.

Définition formelle

Définition en termes de chemins

L'espace tangent \scriptstyle T_xM et un vecteur tangent \scriptstyle v\in T_xM, le long d'une courbe à un point \scriptstyle x\in M

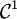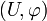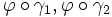Supposons que M est une variété différentielle de dimension n et de classe \mathcal{C}^1 et que p est un point de M. Soit (U,\varphi) une carte locale de M en p. Deux courbes \gamma_1,\gamma_2:]-1,1[\rightarrow M, telles que \varphi\circ\gamma_1, \varphi\circ\gamma_2 soient différentiables en 0, sont dites tangentes en 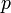\,p si γ1(0) = γ2(0) = p et 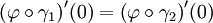\big(\varphi\circ\gamma_1\big)^\prime(0) = \big(\varphi\circ\gamma_2\big)^\prime(0) . Cette relation est une relation d'équivalence. L'ensemble des classes est l'espace tangent en p à M, noté Tp(M). La fonction 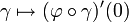\gamma\mapsto (\varphi\circ\gamma)'(0) induit par passage au quotient une bijection de Tp(M) dans \mathbb{R}^n qui fait de l'espace tangent un espace vectoriel. La formule du changement de cartes montre que la structure vectorielle ne dépend pas de la carte locale choisie.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Espace tangent ».

Wikimedia Foundation. 2010.

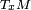
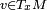Contenu soumis à la licence CC-BY-SA. Source : Article Vecteur tangent de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • vecteur tangent — liestinis vektorius statusas T sritis fizika atitikmenys: angl. tangent vector; tangential vector vok. Tangentenvektor, m; Tangentialvektor, m rus. касательный вектор, m; тангенциальный вектор, m pranc. vecteur tangent, m …   Fizikos terminų žodynas

  • Vecteur tangent à une courbe — ● Vecteur tangent à une courbe pointeur dont l origine est le point de contact de la tangente avec la courbe considérée, et le vecteur, un vecteur directeur de cette tangente …   Encyclopédie Universelle

  • Vecteur de killing — En mathématiques, un vecteur de Killing[1], ou champ de Killing, est un champ vectoriel sur une variété riemannienne qui conserve la métrique de cette variété. Le nom de vecteur de Killing est donné en l honneur du mathématicien allemand Wilhelm… …   Wikipédia en Français

  • tangent — tangent, ente [ tɑ̃ʒɑ̃, ɑ̃t ] adj. • 1683; lat. tangens, entis, de tangere « toucher » 1 ♦ Géom. Qui n a qu un point de contact en un seul point. (1705) Plan tangent à une surface : ensemble des tangentes en un point à cette surface, formant… …   Encyclopédie Universelle

  • Vecteur de killing conforme — En géométrie riemannienne, un vecteur de Killing conforme ou un champ de vecteurs de Killing conforme ou un champ conforme est un champ de vecteurs correspondant à une variation infinitésimale d une isotopie conforme pour une métrique… …   Wikipédia en Français

  • Vecteur de Killing — En mathématiques, un vecteur de Killing[1], ou champ de Killing, est un champ vectoriel sur une variété riemannienne qui conserve la métrique de cette variété. Le nom de vecteur de Killing est donné en l honneur du mathématicien allemand Wilhelm… …   Wikipédia en Français

  • Vecteur de Killing conforme — En géométrie riemannienne, un vecteur de Killing conforme ou un champ de vecteurs de Killing conforme ou un champ conforme est un champ de vecteurs correspondant à une variation infinitésimale d une isotopie conforme pour une métrique… …   Wikipédia en Français

  • tangent vector — liestinis vektorius statusas T sritis fizika atitikmenys: angl. tangent vector; tangential vector vok. Tangentenvektor, m; Tangentialvektor, m rus. касательный вектор, m; тангенциальный вектор, m pranc. vecteur tangent, m …   Fizikos terminų žodynas

  • Vecteur normal — Normale à une surface Un plan et deux vecteurs normaux. En géométrie, la droite normale à une surface en un point est la droite orthogonale au plan tangent en ce point. Les vecteurs directeurs de cette droite sont appelés vecteurs normaux à la… …   Wikipédia en Français

  • Espace Tangent — L espace tangent en un point a d une variété différentielle M est un espace vectoriel qui intuitivement est l ensemble de tous les vecteurs vitesse possibles d un mobile se déplaçant (sans pouvoir la quitter) dans la variété M quand il est en a.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”