Pyramidaux

 Cet article concerne les pyramides en tant que polyèdres géométriques. Pour les autres significations, voir Pyramide (homonymie).

Ensemble des pyramides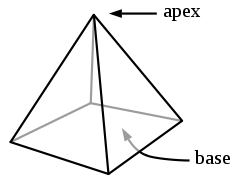
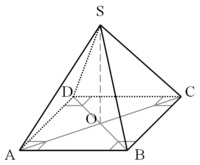
Faces	n triangles, 1 n-gone
Arêtes	2n
Sommets	n+1
Groupe de symétrie	Cnv
Polyèdre dual	Auto-duaux
Propriétés	convexe

Une pyramide (du grec pyramis) à n cotés est un polyèdre formé en reliant une base polygonale de n cotés à un point, appelé l'apex, par n faces triangulaires (n ≥ 3). En d'autres mots, c'est un solide conique avec une base polygonale.

Lorsque cela n'est pas précisé, la base est supposée carrée. Pour une pyramide triangulaire chaque face peut servir de base, avec le sommet opposé pour apex. Le tétraèdre régulier, un des solides de Platon, est une pyramide triangulaire. Les pyramides carrées et pentagonales peuvent aussi être construites avec toutes les faces régulières, et par conséquent sont des solides de Johnson. Toutes les pyramides sont des auto-duaux.

Les pyramides sont une sous-classes des prismatoïdes.

Origine du nom

Ce sont les Grecs qui ont introduit le nom de « pyramide », comparant les pyramides d'Égypte avec une de leurs pâtisseries de forme similaire appelée « pyramis » ou « pyramous »^[1].

Volume

Le volume d'une pyramide est 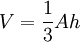où A est l'aire de la base et h la hauteur de la base à l'apex. Ceci est valable pour toute localisation de l'apex, à condition que h soit mesuré comme la distance perpendiculaire à partir du plan qui contient la base.

Ceci peut être démontré par le calcul suivant :

En utilisant le fait que les dimensions d'une section plane parallèle à la base augmente de façon linéaire à partir de l'apex vers la base. Alors, la section plane à une hauteur quelconque y est la base mise à l'échelle par un facteur de 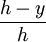, où h est la hauteur à partir de la base vers l'apex. Puisque l'aire d'une forme quelconque est multipliée par le carré de la forme mise à l'échelle, l'aire de la section plane à une hauteur y est .

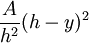Le volume est donné par l'intégrale

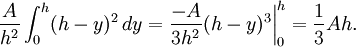
(Trivialement, le volume d'une pyramide à base carrée avec un apex d'hauteur égale à la moitié de la base peut être vue comme un sixième d'un cube formé par six pyramides de cette sorte (en paires opposées) par le centre. Alors "base fois la hauteur" correspond à un demi du volume du cube, et par conséquent trois fois le volume de la pyramide, ce qui donne le facteur un tiers).

Aire de la surface

L'aire de la surface d'une pyramide régulière, c'est-à-dire une pyramide dont toutes les faces sont des triangles isocèles identiques, est 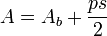où A_b est l'aire de la base, p le périmètre de la base et s la hauteur de la pente le long de la bissectrice d'une face (ie la longueur à partir du milieu d'une arête quelconque de la base jusqu'à l'apex).

Pyramides avec des faces polygonales

Si toutes les faces sont des polygones réguliers, la base de la pyramide peut être un polygone régulier de 3, 4 ou 5 cotés :

Nom	Tétraèdre	Pyramide carrée	Pyramide pentagonale
Classe	Solide de Platon	Solide de Johnson (J1)	Solide de Johnson (J2)
Base	Triangle équilatéral	Carré	Pentagone régulier
Groupe de symétrie	Td	C4v	C5v

Le centre géométrique d'une pyramide carrée est localisé sur l'axe de symétrie, à un quart de la base vers l'apex.

Symétrie

Si la base est régulière et l'apex est au-dessus du centre, le groupe de symétrie d'une pyramide à n cotés est C_nv d'ordre 2n, excepté dans le cas d'un tétraèdre régulier, qui possède le groupe de symétri plus grand T_d d'ordre 24, qui a quatre versions de C_3v pour sous-groupes.

Le groupe de rotation est C_n d'ordre n, excepté dans le cas d'un tétraèdre régulier, qui possède le groupe de rotation plus grand T d'ordre 12, qui a quatre versions de C₃ pour sous-groupes.

Généralisation aux dimensions supérieures

Une pyramide est un objet géométrique ayant pour base un polygone quelconque, auquel on relie tous ses sommets à un point unique. Par abus de langage, on dit qu'elle est régulière si toutes ses faces sont des polygones réguliers.

En généralisant, une hyperpyramide de dimension 4 est un polychore ayant pour base un polyèdre auquel on relie tous ses sommets à un point unique. Le pentachore en est l'exemple le plus simple.

Et donc, une hyperpyramide de dimension n est un polytope à n dimensions, qui a pour base un polytope à n-1 dimensions, et dont tous les sommets sont reliés à un point unique. Une hyperpyramide peut être considérée comme l'ensemble de tous les "états" pris par sa base lors de son rétrécissement progressif jusqu'à l'apex le long d'une médiane centrale (reliant le centre de gravité de la base au sommet); tous ces "états" de la base sont en fait l'intersection de l'hyperpyramide avec des hyperplans parallèles à la base. L'hypervolume d'une hyperpyramide de dimension n est donné par la formule : 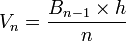,où B_{n − 1} est l'hypervolume de la base et h la hauteur.

Les premières hyperpyramides

Nom	Point	Segment	Triangle	Pyramide	4-hyperpyramide	5-hyperpyramide
Explication	rien (d=-1) n'est relié à un point (d=0)	un point (d=0) est relié à un point (d=0)	un segment (d=1) est relié à un point (d=0)	un polygone (d=2) est relié à un point (d=0)	un polyèdre (d=3) est relié à un point (d=0)	un polychore (d=4) est relié à un point (d=0)
Dimension	0	1	2	3	4	5
Image

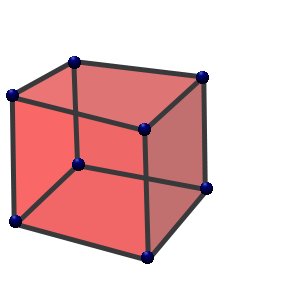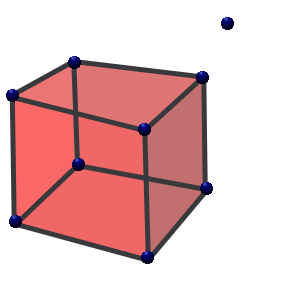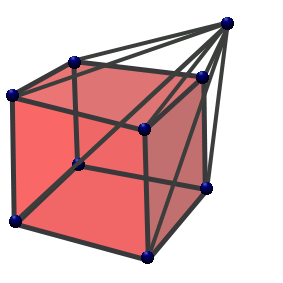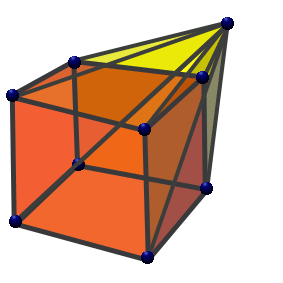
Tout simplexe est une hyperpyramide, et la plus simple de chaque dimension.

Symbolique

La forme pyramidale serait magique, et augmenterait certaines qualités en elle, à un endroit précis.

Notes, références

Article connexe

• Bipyramide
• Pyramides d'Égypte
• Pyramide du Louvre

Liens externes

• Les polyèdres uniformes
• Pyramide triangulaire, Pyramide carrée et Pyramide pentagonale en rotation sur le site Math Is Fun
• Polyèdres en réalité virtuelle L'encyclopédie des polyèdres
  • Modèles VRML (George Hart) <3> <4> <5>
• Patrons en papier de pyramides

• Portail de la géométrie