- Polychore
-
4-polytope régulier convexe
 Un hypercube en rotation
Un hypercube en rotation
En mathématique, un polytope régulier convexe à 4 dimensions (ou polychore) est un polytope à 4 dimensions qui est à la fois régulier et convexe. Ce sont les analogues en 4 dimensions des solides de Platon (3 dimensions) et des polygones réguliers (2 dimensions).
Ces polytopes furent décrits la première fois par le mathématicien suisse Ludwig Schläfli au milieu du XIXe siècle. Schläfli découvrit qu'il y avait précisément six figures de ce type. Cinq d'entre elles sont considérées comme les analogues de dimension 4 des solides de Platon. Il y a une figure supplémentaire (l'icositétrachore) qui n'a aucun équivalent tri-dimensionnel.
Chaque polytope régulier convexe à 4 dimensions est limité par des cellules tri-dimensionnelles qui sont toutes des solides de Platon du même type et de même taille. Ceux-ci sont organisés ensemble le long de leur côtés de manière régulière.
Ils sont tous homéomorphes à une hypersphère à la surface tri-dimensionnelle, leur caractéristique d'Euler-Poincaré vaut donc 0.
Sommaire
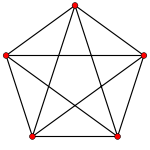
Pentachore
 Un pentachore en rotation
Un pentachore en rotation
Le pentachore est le simplexe régulier de dimension 4. Son symbole de Schläfli est {3,3,3}.
Ses autres noms sont : 5-cellules, pentatope, hyperpyramide à base tétraèdrique, hypertétraèdre, 4-simplexe.
Ses éléments sont :
- 5 Sommets
- 10 Arêtes
- 10 Faces triangulaires
- 5 cellules tétraèdriques
Comme tous les simplexes, il est son propre dual. Il fait partie du groupe de symétrie A4. Sa figure de sommet est un tétraèdre.
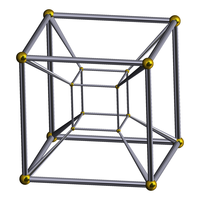
Tesseract
C'est un hypercube à 4 dimensions. Son symbole de Schläfli est {4,3,3}.
Ses autres noms sont : l'octachore, le 8-cellules, le 4-cube.
Ses éléments sont :
- 16 sommets
- 32 arêtes
- 24 faces carrées
- 8 cellules cubiques
Son dual est le 16-cellules (un hypercube est en effet toujours dual d'un hyperoctaèdre et vice-versa). Il fait partie du groupe de symétrie B4. Sa figure de sommet est un tétraèdre.
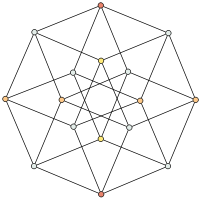
Hexadécachore
 Un hyperoctaèdre en rotation
Un hyperoctaèdre en rotation
C'est un hyperoctaèdre à 4 dimensions. Son symbole de Schläfli est {3,3,4}.
Ses autres noms sont : le 16-cellules, le 4-orthoplexe, le 4-octaèdre.
Ses éléments sont :
- 8 sommets
- 24 arêtes
- 32 faces triangulaires
- 16 cellules tétraèdriques
Il peut être considéré comme une double hyperpyramide à base octaédrique.
Son dual est le tesseract (un hyperoctaèdre est en effet toujours dual d'un hypercube et vice-versa). Il fait partie du groupe de symétrie B4. Sa figure de sommet est un octaèdre.
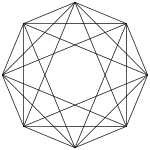
Icositétrachore
Il n'a aucun analogue en 3 dimensions. Son symbole de Schläfli est {3,4,3}.
Ses autres noms sont : le 24-cellules, l'octaplexe, le poly-octaèdre.
Ses éléments sont :
- 24 sommets
- 96 arêtes
- 96 faces triangulaires
- 24 cellules octaèdriques
Ayant autant de sommets que de cellules, et autant d'arêtes que de faces, il est son propre dual. Il fait partie du groupe de symétrie F4. Sa figure de sommet est un cube.
Hecatonicosachore
Il est l'analogue quadri-dimensionnel du dodécaèdre régulier. Son symbole de Schläfli est {5,3,3}.
Ses autres noms sont : l'hécatonicosaédroïde, le 120-cellules, le dodécaplexe, l'hyperdodécaèdre, le polydodécaèdre.
Ses éléments sont :
- 600 sommets
- 1200 arêtes
- 720 faces pentagonales
- 120 cellules dodécaèdriques
Son dual est l'hexachosichore, de la même façon que l'icosaèdre était le dual du dodécaèdre. Son groupe de symétrie est H4. Sa figure de sommet est un tétraèdre.
Hexacosichore
Il est l'analogue quadri-dimensionnel de l'icosaèdre régulier. Son symbole de Schläfli est {3,3,5}.
Ses autres noms sont : le 600-cellules, le tétraplexe, l'hypericosaèdre, le polytétraèdre.
Ses éléments sont :
- 120 sommets
- 720 arêtes
- 1200 faces triangulaires
- 600 cellules tétraèdriques
Son dual est l'hecatonicosachore, de la même façon que le dodécaèdre était le dual de l'icosaèdre. Son groupe de symétrie est H4. Sa figure de sommet est un icosaèdre.
Notes et références
Voir aussi
Articles connexes
Liens externes
- Les polychores réguliers sur le site Mathcurve
- Les dimensions sur le site Dimensions-Superieures
- Sur Mathworld (en anglais)
- Patrons des polychores réguliers (en anglais)
- Le film documentaire "dimensions" donne des moyens de s'imaginer ces objets
- Les polychores réguliers sur Eusebeia (en anglais)
Bibliographie
- H. S. M. Coxeter, Introduction to Geometry, 2nd ed., John Wiley & Sons Inc., 1969. ISBN 0-471-50458-0.
- H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8.
- D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
- Portail de la géométrie
Catégorie : Polytope
Wikimedia Foundation. 2010.