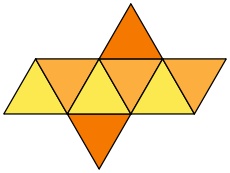
- Octaèdre
-
Octaèdre 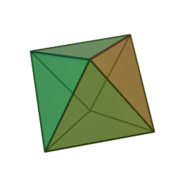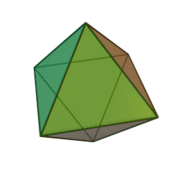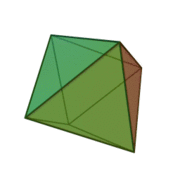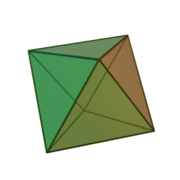
Type Polyèdre régulier Faces Triangle Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
8
12
6
2Faces par sommet 4 Sommets par face 3 Isométries Dual Cube Propriétés Deltaèdre régulier et convexe modifier 
Un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces. Si ses faces sont triangulaires, il possède alors douze arêtes et six sommets.
Par exemple, une pyramide heptagonale est un octaèdre, dont les huit faces sont sa base heptagonale et ses sept faces triangulaires : 1 + 7 = 8. Puisque 2 + 6 = 8, une infinité de prismes sont des octaèdres, dont deux faces sont des hexagones.
Sommaire
L'octaèdre régulier
Un octaèdre régulier est un solide de Platon composé de huit faces dont chacune est un triangle équilatéral, se joignant quatre à quatre à chaque sommet. Platon, dans ses travaux, a voulu expliquer la matière par cinq éléments, et a utilisé des polyèdres réguliers pour les symboliser, l'octaèdre représentait l'élément « air »[1].
L'aire A et le volume V de l'octaèdre régulier d'arête a valent respectivement :
L'octaèdre régulier est un genre spécial d'antiprisme triangulaire et de bipyramide carrée.
C'est aussi le dual du cube, c'est-à-dire que c'est le polyèdre obtenu en prenant pour sommets les centres des faces d'un cube, et en joignant les sommets qui correspondent à des faces adjacentes. En conséquence, on peut faire correspondre aux sommets et aux faces de l'octaèdre les faces et les sommets du cube.
Les coordonnées canoniques pour les sommets d'un octaèdre centré à l'origine sont (±1,0,0), (0, ±1, 0), (0,0,±1).
Comme il a trois sommets par face, et quatre faces par sommet, son symbole de Schläfli est {3,4}.
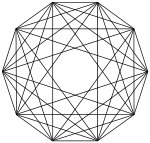
Le squelette de l'octaèdre régulier, l'ensemble de ses sommets reliés par ses arêtes, forme un graphe appelé graphe octaédrique.
Généralisation
L'hyperoctaèdre (ou polytope croisé, ou orthoplexe, ou encore n-octaèdre) est la généralisation de l'octaèdre en n dimensions.
Le n-octaèdre est le dual du n-cube (hypercube à n dimensions) : pour obtenir un n-octaèdre on relie entre eux les centres des faces (de dimension n-1) d'un n-cube.
L'hyperoctaèdre est, avec l'hypercube et le n-simplexe, un des trois seuls polytopes existant sous forme régulière dans toute dimension n. Les polytopes réguliers sont en effet une infinité en dimension 2 (voir polygone régulier), 5 en dimension 3 (voir solide de Platon), 6 en dimension 4, et après ils ne sont plus que 3, comme Ludwig Schläfli l'a démontré.
Le symbole de Schläfli d'un n-octaèdre est de la forme {3,3,3,…,3,4} avec (n-1) chiffres.
Les coordonnées des sommets d'un hyperoctaèdre centré à l'origine sont obtenues en permutant les coordonnées (±1,0,0,0,...,0,0).
Les premiers hyperoctaèdres Hyperoctaèdre Carré Octaèdre Hexadécachore ou 16-cellules 5-octaèdre Dimension 2 3 4 5 Sommets 4 6 8 10 Représentation 
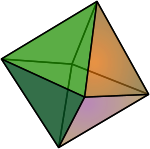

Hypervolume d'un hyperoctaèdre régulier
L'hypervolume d'un polytope est le contenu n-dimensionnel de ce polytope. Soit a son arête.
Pour construire un (n+1)-octaèdre, on relie les 2n sommets d'un n-octaèdre à un nouveau point au-dessus et à un nouveau point au-dessous.
- Ainsi, un segment dont les extrémités sont reliées à un point au-dessus et à un point au-dessous donne un carré (on supposera que les points ont été placés de sorte à donner un hyperoctaèdre régulier).
- Un carré dont les sommets sont reliés à un point au-dessus et à un point au-dessous donne un octaèdre.
- Un octaèdre dont les sommets sont reliés à un point au-dessus et à un point en dessous (situés dans une autre dimension) donne bien un hexadécachore.
L'hyperoctaèdre est donc une double hyperpyramide (à base hyperoctaédrique de dimension inférieure). Etant régulier dans le cas étudié, ses sommets sont tous sur une n-sphère circonscrite. Cette n-sphère circonscrite est également celle de ses faces hyperoctaèdriques de dimensions inférieures, car tous les sommets de l'hyperoctaèdre régulier sont dessus. Le rayon du centre de cette n-sphère aux sommets est donc le même pour toute dimension n :

L'hypervolume est celui de deux hyper-pyramides de hauteur Rn. On en déduit donc que l'hypervolume (le n-contenu) d'un n-octaèdre régulier d'arête a vaut :

Exemples :
- Aire du carré :

- Volume de l'octaèdre régulier :

- Hypervolume de l'hexadécachore :

...
(On suppose dans cette formule que le seul n-octaèdre à ne pas avoir une longueur d'arête égale à a est le segment (1-octaèdre), qui a dans ce cas pour longueur
 (diagonale d'un carré) pour donner bien un carré de côté a avec la méthode de construction donnée)
(diagonale d'un carré) pour donner bien un carré de côté a avec la méthode de construction donnée)L'octaèdre articulé
Il existe des octaèdres flexibles, ce sont les polyèdres déformables de taille minimale. Comme l'a prouvé Cauchy, ils ne peuvent pas être convexes[2].
Annexes
Bibliographie
- (en) H. S. M. Coxeter, Regular Polytopes, New York, Dover Publications, 1973, 3rd ed.e éd. (ISBN 978-0-486-61480-9) (LCCN 73084364), p. 121–122 p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)
Notes et références
- Les cinq éléments de Platon : Histoire du solide de Platon
- Voir Bricard R. Mémoire sur la théorie de l'octaèdre articulé, in Journal de Mathématiques pures et appliquées, Liouville, tome 3:113-148, 1897
Voir aussi
Articles connexes
- L'octaèdre régulier est un :
- Autres polytopes :
Liens externes
- Articles MathWorld (en anglais) :
Wikimedia Foundation. 2010.