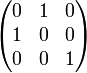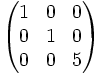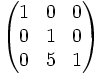Matrice Élémentaire

Matrice Élémentaire

Matrice élémentaire

Une matrice est dite élémentaire lorsqu'elle est obtenue par des opérations élémentaires sur les lignes ou colonnes de la matrice identité.

Les opérations élémentaires sur une matrice sont les suivantes :

  • échanger deux lignes ou deux colonnes
  • ajouter un multiple d'une ligne à une autre ligne (respectivement colonne)
  • multiplier une ligne ou une colonne par un scalaire différent de zéro

Exemples

Opération effectuée sur la matrice identité I3 type de matrice
permutation ligne 1 et 2 \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} matrice de permutation
ligne n°3 * 5 \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 5 \\ \end{pmatrix} matrice de dilatation
ligne n°3 + 5*ligne n°2 \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 5 & 1 \\ \end{pmatrix} matrice de transvection

Multiplier à gauche une matrice A par une matrice élémentaire revient à effectuer l'opération élémentaire correspondante sur les lignes de A. Multiplier A à droite par une matrice élémentaire revient à faire une opération sur les colonnes.

Voir aussi

Ce document provient de « Matrice %C3%A9l%C3%A9mentaire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice Élémentaire de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Matrice elementaire — Matrice élémentaire Une matrice est dite élémentaire lorsqu elle est obtenue par des opérations élémentaires sur les lignes ou colonnes de la matrice identité. Les opérations élémentaires sur une matrice sont les suivantes : échanger deux… …   Wikipédia en Français

  • Matrice élémentaire — Une matrice est dite élémentaire lorsqu elle est obtenue en appliquant une seule opération élémentaire sur les lignes ou colonnes de la matrice identité[1]. Les opérations élémentaires sur une matrice sont les suivantes[2] : permuter deux… …   Wikipédia en Français

  • Matrice De Permutation — Une matrice de permutation est une matrice carrée qui vérifie les propriétes suivantes : les coefficients sont 0 ou 1 ; il y a un et un seul 1 par ligne ; il y a un et un seul 1 par colonne. Ainsi : est une matrice de… …   Wikipédia en Français

  • Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice De Vandermonde — En algèbre linéaire, une matrice de Vandermonde est une matrice avec une progression géométrique dans chaque ligne. Elle tient son nom d Alexandre Théophile Vandermonde. Sommaire 1 Présentation 2 Inversibilité 3 Déterminant …   Wikipédia en Français

  • Matrice de vandermonde — En algèbre linéaire, une matrice de Vandermonde est une matrice avec une progression géométrique dans chaque ligne. Elle tient son nom d Alexandre Théophile Vandermonde. Sommaire 1 Présentation 2 Inversibilité 3 Déterminant …   Wikipédia en Français

  • Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D …   Wikipédia en Français

  • Matrice Inversible — En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In suffit d aprés le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”