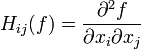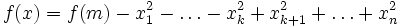Matrice de Hesse

Matrice de Hesse

Matrice hessienne

En mathématiques, la matrice hessienne d'une fonction numérique f est la matrice carrée, notée H(f), de ses dérivées partielles secondes.

Plus précisément, étant donnée une fonction f à valeurs réelles

f(x1, x2, ..., xn),

et en supposant que toutes les dérivées partielles secondes de f existent, le coefficient d'indice i,j de la matrice hessienne de f vaut

H_{ij}(f) = \frac{\partial^2 f}{\partial x_i\partial x_j}

ou, en d'autres termes,

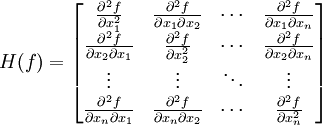H(f) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\partial x_n} \\ \frac{\partial^2 f}{\partial x_2\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n\partial x_1} & \frac{\partial^2 f}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} .

On appelle hessien (ou discriminant hessien) le déterminant de cette matrice.

Le terme « hessien » a été introduit par James Joseph Sylvester, en hommage au mathématicien allemand Ludwig Otto Hesse.

Soit notamment f une fonction de classe 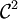\mathcal C^2 définie sur un ouvert U de l'espace E, à valeurs réelles. Sa matrice hessienne est bien définie et en vertu du théorème de Schwarz, elle est symétrique.

Sommaire

Application à l'étude des points critiques

Point selle

On suppose f fonction de classe 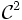{\mathcal C}^2 sur un ouvert U. La matrice hessienne permet, dans de nombreux cas, de déterminer la nature des points critiques de la fonction f, c'est-à-dire des points d'annulation du gradient.

Précisément, un point critique de f est dit dégénéré lorsque le discriminant hessien s'annule. Lorsque les points critiques sont non dégénérés, le signe des valeurs propres détermine la nature du point critique.

  • si la matrice est définie positive, le point constitue un minimum
  • si elle est définie négative, il s'agit d'un maximum
  • s'il y a des valeurs propres de chaque signe, on a affaire à un point selle.

Dans ce dernier cas, on définit l'indice du point critique comme le nombre de valeurs propres négatives.

En dimension deux notamment, le discriminant hessien étant le produit des valeurs propres, son signe suffit à déterminer la nature d'un point critique non dégénéré.

Enfin pour un point critique dégénéré, aucune de ces implications n'est vraie. Un des exemples les plus simples de point critique dégénéré est la selle de singe.

Extension au cadre des variétés

Lorsque M est une variété différentielle et f une fonction numérique indéfiniment différentiable sur M, il est possible de définir la différentielle de f en tout point, mais pas la matrice hessienne, comme on le voit en écrivant une formule de changement de cartes.

Cependant, lorsque m est un point critique pour la fonction f, la matrice hessienne de f en m peut effectivement être définie. On peut donc parler de point critique dégénéré ou non et prolonger les résultats du paragraphe précédent.

Lemme de Morse

Le lemme de Morse[1] montre que le comportement d'une fonction régulière au voisinage d'un point critique non dégénéré est entièrement déterminé par la connaissance de l'indice du point critique.

Lemme de Morse — Soit f une fonction 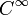C^\infty sur une variété différentielle de dimension n. On considère un point critique non dégénéré m pour la fonction f, et on note k son indice. Alors il existe un système de coordonnées locales 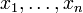x_1, \dots, x_n centré en m et tel que l'expression correspondante de f est

f(x)=f(m)-x_1^2-\dots -x_k^2 +x_{k+1}^2+\dots +x_n^2

On qualifie un tel système de coordonnées de Morse.

Il résulte notamment du lemme que les points critiques non dégénérés sont isolés.

Théorie de Morse

Article détaillé : Théorie de Morse.

Une fonction dont tous les points critiques sont non dégénérés est qualifiée de fonction de Morse. La théorie de Morse a pour objectif de relier l'étude de la topologie de la variété à celle des points critiques des fonctions qui peuvent y être définies.

Notes et références de l'article

  1. ↑ (en) John Milnor, Morse Theory, Princeton University Press, 1963. ISBN 0-691-08008-9, p. 6.

Voir aussi

Articles connexes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Matrice hessienne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice de Hesse de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Matrice Hessienne — En mathématiques, la matrice hessienne d une fonction numérique f est la matrice carrée, notée H(f), de ses dérivées partielles secondes. Plus précisément, étant donnée une fonction f à valeurs réelles f(x1, x2, ..., xn), et en supposant que… …   Wikipédia en Français

  • Matrice hessienne — En mathématiques, la matrice hessienne (ou simplement la hessienne) d une fonction numérique f est la matrice carrée, notée H(f), de ses dérivées partielles secondes. Plus précisément, étant donnée une fonction f à valeurs réelles f(x1, x2, ...,… …   Wikipédia en Français

  • Otto Hesse — Ludwig Otto Hesse Ludwig Otto Hesse Ludwig Otto Hesse (né le 22 avril 1811 – mort le 4 août 1874) est un mathématicien Allemand. Il est né à Königsberg, en Prusse (désormais Kaliningrad en Russie) et est mort à …   Wikipédia en Français

  • Ludwig Otto Hesse — (22 avril 1811 à Königsberg, Prusse – 4 août 1874 à Munich, Allemagne) est un mathématicien allemand qui a travaillé sur les invariants algébriques. Il a donné son nom à la courbe de Hesse, à la matrice hessienne et à la forme normale de …   Wikipédia en Français

  • Discriminant hessien — Matrice hessienne En mathématiques, la matrice hessienne d une fonction numérique f est la matrice carrée, notée H(f), de ses dérivées partielles secondes. Plus précisément, étant donnée une fonction f à valeurs réelles f(x1, x2, ..., xn), et en… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Cuivre — Pour les articles homonymes, voir Cu et Cuivre (homonymie). Cuivre Nic …   Wikipédia en Français

  • Archetype (psychanalyse) — Archétype (psychologie analytique) Pour les articles homonymes, voir Archétype. L archétype est une forme a priori de toute expérience humaine, inscr …   Wikipédia en Français

  • Archétype (Psychanalyse) — Archétype (psychologie analytique) Pour les articles homonymes, voir Archétype. L archétype est une forme a priori de toute expérience humaine, inscr …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”