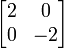Point selle

Point selle

Point col

Le point en rouge est un point col pour la fonction (ici la fonction z=x2−y2).

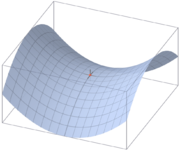
En mathématiques, un point col (en anglais saddle point) pour une fonction f de plusieurs variables à valeurs dans \R désigne un point en lequel les dérivées de la fonction s'annulent (un point critique), sans pour autant que le point soit un extremum local (minimum ou maximum) de la fonction.

Le nom point col vient de la représentation du graphe de la fonction f qui ressemble au col d'une chaîne montagneuse. Dans (au moins) une direction, le point col est un maximum (pour passer d'une vallée à l'autre) et dans (au moins) une autre direction, c'est un minimum (pour passer d'une montagne à l'autre). Ce n'est donc pas un extremum local car selon la direction prise, il existe des points pour lesquels la valeur de la fonction est supérieure ou inférieure à la valeur de la fonction au point col. L'exemple de la figure est le cas le plus simple de point col qui existe.

Le terme point selle est aussi usité (il fait référence à la forme de la selle de cheval). Il existe un type particulier de point col dit en selle de singe pour lequel il y a 3 versants en descente (où pour reprendre l'analogie de la selle : deux pans pour mettre les pattes du singe et un troisième pour la queue).

En une dimension, un point col est un point d'inflexion.

D'une manière plus générale, un point col pour une fonction est un point critique dans le voisinage duquel la courbe n'est pas d'un seul côté de l'hyper-plan tangent.

Utilisation de la hessienne

Une méthode pour déterminer si un point critique d'une fonction de deux variables à valeurs réelles F(x,y) est un point col, consiste à calculer la matrice hessienne en ce point. Si la hessienne a des valeurs propres de signes différents, alors le point est un point col.

Par exemple, la hessienne de la fonction f(x,y) = x2 − y2 au point critique (0,0) est la matrice

\begin{bmatrix} 2 & 0\\ 0 & -2 \\ \end{bmatrix}

qui a une valeur propre strictement positive (2), et une valeur propre strictement négative (-2). Par conséquent, (0,0) est un point col.

Ce critère ne donne pas de condition nécessaire : pour la fonction g(x,y) = x4 − y4, le point (0,0) est un point col mais la hessienne est la matrice nulle. Donc la hessienne n'a pas de valeur propre positive et négative.

Lien interne

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Point col ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Point selle de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Point de lagrange — Pour les articles homonymes, voir Lagrange. Un point de Lagrange (noté L1 à L5), ou, plus rarement, point de libration, est une position de l espace où les champs de gravité de deux corps en orbite l un autour de l autre, et de masses… …   Wikipédia en Français

  • Point de libration — Point de Lagrange Pour les articles homonymes, voir Lagrange. Un point de Lagrange (noté L1 à L5), ou, plus rarement, point de libration, est une position de l espace où les champs de gravité de deux corps en orbite l un autour de l autre, et de… …   Wikipédia en Français

  • Point-col — Le point en rouge est un point col pour la fonction (ici la fonction z=x2−y2). En mathématiques, un point col (en anglais saddle point) pour une fonction f de plusieurs variables à valeurs dans …   Wikipédia en Français

  • Point critique (mathematiques) — Point critique (mathématiques) En analyse à plusieurs variables, un point critique d une fonction de plusieurs variables, à valeurs numériques, est un point d annulation de son gradient. Les points critiques servent d intermédiaire pour la… …   Wikipédia en Français

  • Point col — Le point en rouge est le point du graphe de la fonction associé à son unique point selle (0,0). En mathématiques, un point selle (en anglais saddle point) d une fonction f définie sur un produit cartésien …   Wikipédia en Français

  • Point de Lagrange — Pour les articles homonymes, voir Lagrange. Un point de Lagrange (noté L1 à L5), ou, plus rarement, point de libration, est une position de l espace où les champs de gravité de deux corps en orbite l un autour de l autre, et de masses… …   Wikipédia en Français

  • Point critique (mathématiques) — En analyse à plusieurs variables, un point critique d une fonction de plusieurs variables, à valeurs numériques, est un point d annulation de son gradient. Les points critiques servent d intermédiaire pour la recherche des extremums d une telle… …   Wikipédia en Français

  • Selle (equitation) — Selle (équitation) Pour les articles homonymes, voir selle. La selle désigne un objet, généralement en cuir, placé sur le dos d un cheval et sur lequel le cavalier s assoit …   Wikipédia en Français

  • sellé — sellé, ée 1. (sè lé, lée) part. passé de seller1. •   Le prince d Orange est si sévère dans son armée, qu il n y a point de colonel qui ose se déshabiller pour dormir, ni dormir qu avec un cheval sellé et bridé à ses côtés, PELLISSON Lett. hist.… …   Dictionnaire de la Langue Française d'Émile Littré

  • Selle (équitation) — Pour les articles homonymes, voir selle. La selle désigne un objet, généralement en cuir, placé sur le dos d un cheval et sur lequel le cavalier s assoit. Cheval sellé …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”