Grand dodecicosidodecaedre
- Grand dodecicosidodecaedre
-
Grand dodécicosidodécaèdre
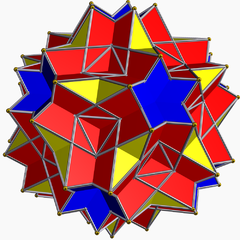
En géométrie, le grand dodécicosidodécaèdre est un polyèdre uniforme non-convexe, indexé sous le nom U61.
Il partage son arrangement de sommets, son arrangement d'arêtes ainsi que ses faces triangulaires et pentagrammiques avec le grand rhombicosidodécaèdre uniforme.
Voir aussi
Lien externe
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Grand dodecicosidodecaedre de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Grand Dodécicosidodécaèdre — Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par cotés 20{3}+12{5/2}+12{10 … Wikipédia en Français
Grand dodécicosidodécaèdre — Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par côtés 20{3}+12{5/2}+12{10/3} … Wikipédia en Français
Grand Dodécicosidodécaèdre Adouci — Type Polyèdre uniforme Éléments F=104, A=180, S=60 (χ= 16) Faces par cotés (20+60){3}+(12+12) … Wikipédia en Français
Grand Dodécicosidodécaèdre Ditrigonal — Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par cotés … Wikipédia en Français
Grand dodecicosidodecaedre adouci — Grand dodécicosidodécaèdre adouci Grand dodécicosidodécaèdre adouci Type Polyèdre uniforme Éléments F=104, A=180, S=60 (χ= 16) Faces par cotés (20+60){3}+(12+12) … Wikipédia en Français
Grand dodecicosidodecaedre ditrigonal — Grand dodécicosidodécaèdre ditrigonal Grand dodécicosidodécaèdre ditrigonal Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par cotés … Wikipédia en Français
Grand dodécicosidodécaèdre adouci — Type Polyèdre uniforme Éléments F=104, A=180, S=60 (χ= 16) Faces par côtés (20+60){3}+(12+12){5/2} … Wikipédia en Français
Grand dodécicosidodécaèdre ditrigonal — Type Polyèdre uniforme Éléments F=44, A=120, S=60 (χ= 16) Faces par côtés 20{3}+12{5}+12{10/3} … Wikipédia en Français
Grand Dirhombicosidodécaèdre — Type Polyèdre uniforme Éléments F=124, A=240, S=60 (χ= 56) Faces par cotés 40{3}+60{4}+24{5/2 … Wikipédia en Français
Grand Dirhombidodécaèdre Disadouci — Type Polyèdre uniforme Éléments F=204, A=240, S=60 (χ=32) Faces par cotés 120{3}+60{4}+24{ … Wikipédia en Français