Entier de Dirichlet

Pour les articles homonymes, voir Entier (homonymie).

Dirichlet

En mathématiques, et plus précisément en arithmétique modulaire, nous appellerons^[1] entier de Dirichlet un nombre réel de la forme a + b.ω, ici ω désigne le nombre d'or (¹⁄₂)(1+ $\sqrt 5$ ) et a, b deux entiers relatifs. Sur les nombres de cette nature, il est possible de définir une nouvelle arithmétique. Elle est un peu analogue à celle, plus usuelle, des nombres entiers, décrite dans l'article arithmétique élémentaire. Cette arithmétique est à l'origine de bien des propriétés mathématiques du nombre d'or.

Les entiers de Dirichlet forment un ensemble stable pour l'addition, la soustraction et la multiplication. Il correspond au plus petit ensemble de nombres réels contenant à la fois un et le nombre d'or et stable pour les opérations citées. Sur cet ensemble, il est possible de définir une division euclidienne. On retrouve le lemme d'Euclide, l'identité de Bézout ainsi que le théorème fondamental de l'arithmétique garantissant, en un certain sens l'existence et l'unicité de la décomposition en facteurs premiers d'un entier de Dirichlet. On retrouve les propriétés du plus grand commun diviseur et du plus petit commun multiple et, avec un peu de travail, un équivalent du petit théorème de Fermat. L'analogie ne peut être poussée trop loin, les éléments inversibles pour la multiplication (appelés unités) ne sont pas de même nature dans les deux mondes. À la différence du cas usuel, il n'existe pas deux, mais une infinité de nombres de cette sorte dans l'arithmétique de Dirichlet.

Les entiers de Dirichlet sont utilisés en théorie algébrique des nombres et en arithmétique modulaire, par exemple pour l'étude d'équations diophantiennes. Ces équations sont à coefficients dans les entiers relatifs et les solutions recherchées sont entières. Leur utilisation a permis à Dirichlet et Legendre de démontrer le dernier théorème de Fermat dans le cas où le paramètre est égal à cinq. Les entiers de Dirichlet permettent aussi de résoudre l'équation de Pell-Fermat, encore pour le paramètre cinq.

La relative simplicité de cet univers permet d'élucider sa structure à l'aide des outils de l'arithmétique élémentaire. Ici seuls les théorèmes comme le lemme d'Euclide, l'identité de Bézout ou le petit théorème de Fermat sont utilisés. L'appel à des théories plus puissantes, comme des groupes, des anneaux commutatifs ou des corps finis permet d'aller plus loin. Il devient possible de comprendre des mondes plus vastes, comme ceux des entiers quadratiques. L'ajout d'autres théories comme la théorie de Galois ou celle des Anneaux de Dedekind permet d'appréhender l'entier algébrique dans sa généralité.

Éléments d'histoire

Origines

Leonhard Euler utilise, sans succès, une idée novatrice, à l'origine de l'intérêt pour les entiers de Dirichlet.

L'intérêt pour les propriétés arithmétiques de valeurs analogues au nombre d'or est ancienne. Les indiens de la période classiques développent des outils^[2] comme la fraction continue, ou des méthodes pour l'étude d'équations diophantiennes, c'est-à-dire d'équations à coefficients entiers et dont les solutions recherchées sont entières. Brahmagupta (598 – 668), un des mathématiciens à l'origine du zéro, étudie le cas suivant^[3] :

$x^2 - n\cdot y^2 = 1$

À l'aide d'une identité portant maintenant son nom, il découvre une multiplication entre deux couples de solutions qui donne une troisième solution. Cette méthode, consistant à définir une multiplication sur les couples d'entiers est une des bases de l'arithmétique de Dirichlet.

Plus d'un millénaire plus tard, Leonhard Euler utilise une technique analogue pour une démonstration du dernier théorème de Fermat pour la valeur du paramètre égale à trois. Elle s'avère presque exacte^[4]. À deux couples d'entiers, il associe la multiplication * définie par :

$\forall a,b,c,d \in \mathbb Z\quad (a, b)*(c, d) = (ac -3bd, ad + bc)$

Si cette idée est exactement la même que celle de Brahmagupta, Euler va plus loin. Il remarque que cet ensemble se comporte exactement comme celui des nombres de la forme a + i $\sqrt 3$ .b, ici i désigne l'unité imaginaire. Ceci garantit plusieurs propriétés comme le fait qu'il existe un élément neutre pour la multiplication : un, que cette multiplication est associative, commutative, distributive par rapport à l'addition et que l'ensemble est intègre, c'est-à-dire que si un produit est nul, alors l'un des facteurs du produit est aussi nul. Cet ensemble comporte finalement les mêmes propriétés ainsi que la même limitation que celui des entiers relatifs, à savoir que de nombreux éléments n'ont pas d'inverse pour la multiplication. Cette analogie pousse Euler à appliquer le théorème fondamental de l'arithmétique dans cet univers, c'est-à-dire à utiliser l'existence et l'unicité d'une décomposition d'un entier de cette nature en nombres premiers pour cet univers. Un nombre premier devient ici un nombre qui, s'il est le produit a.b de deux autres nombres, alors soit a soit b est un élément inversible pour la multiplication. Seul 1 est -1 sont inversibles, dans le monde des entiers relatifs. Euler pousse ici l'analogie trop loin, dans ce monde, 2, 1 + i $\sqrt 3$ et 1 - i $\sqrt 3$ seraient des nombres premiers, mais :

$4 = 2\times 2 = (1 + i\sqrt 3)(1 - i\sqrt 3)\;$

Le théorème fondamental de l'arithmétique ne s'applique pas car il existe plusieurs décompositions en facteurs premiers. L'idée est néanmoins promise à un bel avenir.

Disquisitiones Arithmeticae

Disquisitiones Arithmeticae est le livre de Gauss 1801 formalisant les outils à l'origine de la démarche de Dirichlet.

En 1801, Carl Friedrich Gauss publie le traité Disquisitiones Arithmeticae, ouvrant la voie à l'arithmétique moderne et aux idées à l'origine de la richesse de l'arithmétique des entiers de Dirichlet. Un seul outil est manquant dans l'univers d'Euler. Si un monde de cette nature dispose d'une division euclidienne, la démarche est parfaitement pertinente. L'identité de Bézout, le lemme d'Euclide, parfois renommé en lemme de Gauss et le théorème fondamental de l'arithmétique s'applique. Gauss utilise cette approche pour formaliser une nouvelle structure, il considère les restes de la division euclidienne par un élément de l'anneau, ces restes sont appelés modulo. Il montre que cet ensemble dispose aussi d'une addition et d'une multiplication. Cette méthode, d'abord développée sur les entiers relatifs est valide sur tous les anneaux euclidiens. Un anneau est un ensemble équipé de deux lois de composition, l'addition et la multiplication. Ces deux lois vérifient toutes les bonnes propriétés pour autoriser les calculs usuels. Gauss applique ces idées aux nombres de la forme a + i.b, qui forment un anneau euclidien. Un tel nombre est maintenant appelé entier de Gauss.

Gotthold Eisenstein découvre comment contourner la difficulté d'Euler, l'anneau des nombres de la forme a + 1/2(1 + i $\sqrt 3$ ).b est lui euclidien, la démarche d'Euler offre enfin une démonstration rigoureuse pour le grand théorème de Fermat dans le cas du paramètre égal à 3.

Le travail de Dirichlet

La démonstration du cas où le paramètre est égal à 5 s'avère délicate, l'anneau des nombres de la forme a + i $\sqrt 5$ .b n'est pas euclidien et l'idée d'Eisenstein ne permet pas de venir à bout de cette difficulté. Si le dernier théorème de Fermat devient de plus en plus célèbre, les idées pertinentes tardent à venir. Sophie Germain trouve un premier résultat pour le cas où le paramètre n et 2.n + 1 sont deux nombres premiers, le cas n = 5 devient celui à traiter en priorité^[5].

Il devient nécessaire de travailler sur des anneaux de nombres réels. Celui contenant les valeurs a + $\sqrt 5$ .b n'est pas euclidien, mais une idée analogue à celle d'Eisenstein vient à bout de cette difficulté, il suffit de remplacer $\sqrt 5$ par le nombre d'or, Dirichlet utilise une autre méthode, plus complexe qui démontre un résultat plus faible mais suffisant pour sa démonstration. La réticence des mathématiciens à utiliser ces structures provient d'une difficulté parfaitement connue à l'époque. Elles possèdent une spécificité que Dirichlet qualifie d'obstruction. Un anneau de cette nature contient trop d'unités, c'est-à-dire de nombres qui sont inversibles dans l'anneau. Celui des entiers relatifs en contient deux 1 et -1. L'anneau des entiers de Dirichlet en contient une infinité. Cette obstruction est d'ailleurs ce qui, jadis, poussa Brahmagupta à définir sa multiplication.

Dirichlet finit par la maîtriser suffisamment pour pouvoir travailler dans l'anneau (il choisit en pratique le sous-anneau de nombres de la forme a + $\sqrt 5$ .b avec a et b entiers relatifs). En 1825, il acquiert une célébrité instantanée grâce à un apport majeur dans la résolution du grand théorème si le paramètre est égal à cinq. La démonstration est soumise à l'académie des sciences et Adrien-Marie Legendre est nommé référé. Il lui suffit de quelques mois pour finaliser le travail de Dirichlet^[6].

Structures

Un entier de Dirichlet tire son intérêt de l'ensemble de ses éléments ainsi que les lois de compositions qui s'y appliquent. Le nombre $\sqrt 5$ , en tant qu'entier de Dirichlet n'est pas inversible. Dans l'ensemble des nombres réels, ou celui des nombres de la forme a + b. $\sqrt 5$ avec a et b rationnels, il l'est. L'entier naturel 19 est un nombre premier dans l'ensemble des nombres relatifs, dans celui des entiers de Dirichlet il est divisible comme le montre le produit 19 = (4 + 3.ω)(7 - 3.ω) et ne peut être qualifié de premier. Il est en conséquence essentiel de considérer les entiers de Dirichlet comme un tout, munis de ses propriétés propres.

Définitions

La démarche est analogue à celle définissant les entiers quadratiques, elle correspond à celle des entiers de Gauss ou d'Eisenstein.

Pour mettre en évidence cette analogie, le nombre d'or 1/2.(1 + $\sqrt 5$ ) est ici, et dans le reste de l'article désigné par la lettre ω, souvent utilisé dans ce type de situation. Comme le terme d'entier désigne ici parfois un entier quadratique et parfois un entier relatif, l'usage des lettres grecques est réservé, dans cet article, aux entiers de Dirichlet et les lettres latines aux entiers relatifs ou aux nombres rationnels. La lettre ε est utilisée pour décrire une unité, c'est-à-dire un élément inversible de l'anneau des entiers de Dirichlet.

Un nombre réel α est dit entier de Dirichlet si et seulement si, il existe deux entiers relatifs a et b tel que α = a + b.ω.

Comme le montre la suite de l'article, l'ensemble des entiers de Dirichlet forme un anneau euclidien. Dans une telle structure les nombres premiers jouent un rôle essentiel. Pour éviter une confusion entre les nombres premiers usuels et ceux de l'anneau de Dirichlet, on utilise le terme suivant dans le reste de l'article :

Un entier de Dirichlet π est dit nombre premier de Dirichlet seulement si toute décomposition de π en deux facteurs entiers de Dirichlet contient un et un seul élément inversible dans l'anneau.

La notion de nombre premier de Dirichlet correspond à celle d'élément premier ou d'élément irréductible. Une difficulté existe dans la définition précédente des nombres premiers, un entier ne se décompose pas de manière unique. Cette difficulté se trouve aussi pour les entiers relatifs. Au sens de la définition précédente, 4 possède deux décompositions en facteurs premiers, 2x2 et -2x-2. Pour cette raison, on définit dans Z, l'ensemble des entiers relatifs, un nombre premier comme un nombre vérifiant non seulement la propriété de la définition précédente mais qui est aussi strictement positif. Dans le cas général, à un nombre irréductible π correspond une classe d'équivalence, celle des éléments de la forme ε.π où ε décrit le groupe des unités, c'est-à-dire le groupe des éléments ayant un inverse dans l'anneau munis de la multiplication. La convention utilisée dans cet article est de n'appeler nombre premier qu'un unique représentant dans chacune des classes. Cette démarche est analogue à celle utilisée pour les entiers relatifs où seul l'entier strictement positif de la classe est considéré comme premier. Ici, le nombre premier considéré dans une classe est celui de la forme a + ω.b tel que a est strictement positif et b de valeur absolue minimale. Cette convention n'est pas générale.

Structure d'anneau

Article détaillé : Entier quadratique.

L'ensemble des entiers de Dirichlet muni de l'addition et de la multiplication forme un anneau, souvent noté Z[ω]. Cette notation décrit, en général, les polynômes dans lequel on a remplacé la variable X par ω. On obtient une expression de la forme a_nωⁿ + a_n-1ω^n-1 + ... + a₁.ω + a₀, ici n désigne un entier positif et les symboles a_i des entiers relatifs. Le terme ω² peut être remplacé par 1 + ω, le terme ω³ par 1 + 2.ω etc... On obtient in fine, une expression de la forme a + b.ω où a et b désignent deux entiers relatifs.

Cette propriété est générale aux entiers d'un corps de nombre (cf l'article Entier algébrique). Il est néanmoins simple de vérifier ici que l'ensemble est un sous-anneau du corps des nombres réels (tout corps est aussi un anneau). On remarque que :

$\omega^2 = \frac 14 (1 + \sqrt 5)^2 = \frac 14(1 + 2\sqrt 5 + 5) = \frac 12(3 + \sqrt 5) = 1 + \omega \;$

Ce qui permet d'établir la stabilité de l'ensemble pour les différentes opérations :

$\forall a_1,a_2,b_1,b_2 \in \mathbb{Z} \quad (a_1+\omega.b_1)-(a_2+\omega.b_2)=(a_1-a_2)+\omega.(b_1-b_2)\in \mathbb{Z}[\omega]$ $\forall a_1,a_2,b_1,b_2 \in \mathbb{Z} \quad (a_1+\omega.b_1).(a_2+\omega.b_2)=(a_1.a_2+b_1.b_2)+\omega.(a_1.b_2+b_1.a_2+b_1.b_2)\in \mathbb{Z}[\omega]$

En tant que sous-anneau du corps R des nombres réels, l'anneau de Dirichlet hérite de certaines propriétés, ainsi l'anneau est intègre et de caractéristique nulle. Dire qu'un anneau est de caractéristique nulle revient à dire qu'une somme de type 1 + 1 + ... + 1 n'est jamais égale à 0. Un anneau de caractéristique nulle contient une copie de Z, l'anneau des entiers relatifs, engendré par l'élément neutre de l'addition.

Corps des fractions

Article détaillé : Corps des fractions.

Il existe une technique générale qui permet de plonger un anneau intègre dans un corps commutatif. Un corps est un anneau dont tous les éléments, à l'exception de 0 l'élément neutre de l'addition, sont inversibles. Le terme plonger signifie que chaque élément de l'anneau est considéré comme un élément du corps. Cette technique est utilisée pour construire Q, le corps des nombres rationnels. Comme pour le cas des entiers relatifs, un élément du corps des fractions de l'anneau des entiers de Dirichlet est obtenu par une fraction de deux entiers de Dirichlet telle que le dénominateur n'est pas nul. Elle est toujours de la forme a + b. $\sqrt 5$ où a et b sont des nombres rationnels. On les appelle dans cet article des rationnels de Dirichlet.

Si α est un rationnel de Dirichlet alors il existe deux rationnels a et b tel que α = a + b. $\sqrt 5$ .

En effet, soient c, d, e et f quatre entiers relatifs tel que e + f.ω soit non nul, (c'est-à-dire soit e soit f est non nul), on obtient :

$\frac {c + d\cdot \omega}{e + f\cdot \omega}= \frac {c + d\cdot \omega}{e + 1/2f + 1/2f\cdot \sqrt 5}=\frac {(c + d\cdot \omega)(e+f -f\cdot\omega)}{e^2 + e\cdot f - f^2}= \frac {ce + cf - df}{e^2 + ef - f^2} + \frac {de -cf}{e^2 + ef - f^2}\omega$

Le terme du dénominateur ne peut être nul car il est le produit de deux facteurs non nuls. Ces égalités démontrent le résultat cherché, en effet :

$\frac {c + d\cdot \omega}{e + f\cdot \omega}= a + b\cdot \omega \quad\text{si}\quad a = \frac {ce + cf - df}{e^2 + ef - f^2} \quad\text{et}\quad b = \frac {de -cf}{e^2 + ef - f^2}$

Si a et b sont deux rationnels, alors a + b. $\sqrt 5$ est un élément du corps des fractions de l'anneau des entiers de Dirichlet.

Pour s'en assurer, le plus simple est de trouver le dénominateur commun à a et à b, l'expression s'écrit alors comme une fraction de numérateur un entier de Dirichlet et de dénominateur un entier relatif, qui est aussi un entier de Dirichlet.

L'ensemble des fractions formées par les entiers de Dirichlet forme un corps. Cette propriété est une conséquence de la définition des opérations sur les fractions. On en déduit que l'ensemble des rationnels de Dirichlet forme un corps, en général noté Q[ $\sqrt 5$ ].

Fonctions remarquables

Application conjuguée

Deux des outils pour l'étude de l'anneau sont constitués de fonctions. La première, notée ici φ, désigne une fonction de Z[ω] dans lui-même, respectant les lois de composition de l'anneau, c'est-à-dire :

$\forall \alpha, \beta \in \mathbb Z[\omega]\quad \varphi(\alpha - \beta) = \varphi(\alpha) - \varphi(\beta)\quad\text{et}\quad \varphi(\alpha \cdot \beta) = \varphi(\alpha) \cdot \varphi(\beta)$

Une application vérifiant ces propriétés est qualifiée de morphisme d'anneau, comme l'application recherchée et aussi une bijection, le terme consacré est automorphisme d'anneau. Une conséquence de la théorie de Galois indique qu'il n'existe qu'un unique automorphisme de Z[ω] différent de l'identité. Un peu de travail permet d'arriver à ce résultat. Pour cela, le plus simple est d'étudier l'image par φ de l'élément $\sqrt 5$ de Z[ω]. Le fait que φ soit un morphisme montre que :

$\varphi ((\sqrt 5)^2 - 5) = \varphi(\sqrt 5)^2 - 5 = 0 \;$

L'image φ( $\sqrt 5$ ) a pour carré 5, il n'existe que deux valeurs possibles, soit $\sqrt 5$ soit - $\sqrt 5$ . Comme les automorphismes laissent stables les éléments neutres de l'addition et de la multiplication φ(1) est nécessairement égal à 1. On en déduit que l'image de 1 + $\sqrt 5$ est égal à lui-même ou 1 - $\sqrt 5$ et, par voie de conséquence, l'image de ω est égal soit à ω soit à 1/2(1 - $\sqrt 5$ ), que l'on note dans cet article ω'. Si l'image de ω est ω, et que l'application est un automorphisme, il est nécessairement égal à l'identité. L'unique automorphisme restant associe à ω la valeur ω' = 1 - ω.

L'application φ, de Z[ω] dans lui-même, définie par l'égalité suivante est appelée application conjuguée de l'anneau des entiers de Dirichlet. Cette application est un automorphisme d'anneau.

$\forall a, b \in \mathbb Z \quad \varphi(a + b\cdot \omega) = a + b\cdot \omega' = (a + b) - b\cdot \omega\;$

Il est aisé de vérifier que φ est bien un automorphisme. Son nom provient de l'analogie avec la configuration des nombres complexes et de son automorphisme conjugué. La situation est un peu la même si l'on compare la racine de 5 avec l'unité imaginaire.

Norme

Article détaillé : Norme (arithmétique).

Une fois encore la situation est un peu analogue à celle des nombres complexes. Un bon outil pour mettre en valeur les propriétés géométriques des nombres complexes, vus comme un plan, est l'application module. À un nombre, elle associe la racine carrée du produit de lui-même et de son conjugué. En arithmétique, la définition doit être un peu modifiée, le produit d'un entier de Dirichlet par son conjugué n'est pas toujours positif. Par exemple la norme de $\sqrt 5$ est égale à -5.

La norme d'un entier de Dirichlet est le produit de cet entier par son conjugué :

$\forall \alpha \in \mathbb Z[\omega] \quad \mathcal N(\alpha) = \alpha \cdot \varphi (\alpha)\;$

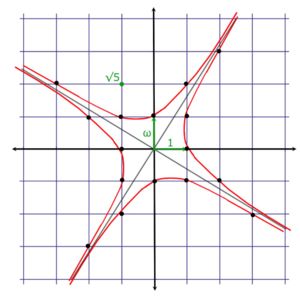
À l'image de la situation complexe ou de celle d'un espace vectoriel, à bien des égard la norme ressemble à une distance. Le cercle de rayon 1, qui serait composé par les entiers de Dirichlet de norme en valeur absolue égale à 1, devient un étrange carré dont les sommets se trouvent repoussés à l'infini et les côtés deviennent des branches d'hyperboles. La figure de droite illustre ce phénomène. Les entiers de Dirichlet sont représentés sur un plan munis d'un repère de centre 0 et de base (1,ω). Cette vision géométrique ressemble à celle d'un espace vectoriel, cependant ici les scalaires ne sont pas des nombres réels mais des entiers relatifs.

La norme possède quelques propriétés clés :

La norme d'un entier de Dirichlet est à valeurs dans l'ensemble des entiers relatifs.

$\forall a,b \in \mathbb Z \quad \mathcal N (a+b\cdot\omega)=a^2+a.b-b^2 \;$

La compatibilité de φ vis-à-vis de la multiplication entraine celle de la norme :

La norme du produit de deux entiers de Dirichlet est égale au produit de la norme des deux entiers.

Cette propriété se démontre aisément :

$\forall \alpha, \beta \in \mathbb{Z}[\omega]\quad \mathcal N (\alpha\cdot \beta) = \alpha\cdot\beta\cdot \varphi(\alpha\cdot \beta) = \alpha\cdot\varphi(\alpha)\cdot \beta\cdot \varphi(\beta)= \mathcal N (\alpha)\cdot\mathcal N (\beta)$

Exprimé à l'aide des coordonnées, on obtient une formule, citée dans l'article nombre d'or et plus délicate à démontrer par un calcul direct :

$(a^2 + ab - b^2)(c^2 + cd - d^2) = (ad + bd)^2 + (ac + bd)(ad + bc + bd) - (ad + bc + bd)^2 \;$

Groupe des unités

Article détaillé : Groupe des unités d'un anneau d'entiers quadratiques.

Norme

Les unités, c'est-à-dire l'ensemble des éléments inversibles pour la multiplication, forment un groupe commutatif pour la multiplication. Dans le cas des entiers de Dirichlet, ce groupe est vaste, ce qui constitue une obstruction. En effet, ces éléments ne sont pas traitables avec les outils classiques de l'arithmétique, avec eux, pas d'identité de Bézout, ni de lemme d'Euclide, de décomposition en facteurs premiers ou de petit théorème de Fermat. En conséquence, il est nécessaire de bien comprendre la structure de ce groupe pour pouvoir le manier sans trop de difficultés. La norme est utile.

Le groupe des unités de l'anneau de Dirichlet est composé des éléments de norme égale à ±1.

En effet, si ε est un entier de Dirichlet de norme égal à ±1, alors soit φ(ε) soit -φ(ε) est l'inverse de ε, ce qui montre que ε est bien une unité. Réciproquement si ε est une unité, alors :

$\mathcal N(\epsilon\epsilon^{-1}) = \mathcal N(\epsilon)\mathcal N(\epsilon)^{-1} = \mathcal N(1) = 1$

La norme de ε est un entier relatif inversible, il n'en existe que deux, 1 et -1, ce qui montre la réciproque.

Déterminer le groupe des unités revient à résoudre l'équation suivante :

$x^2 + xy - y^2 = \pm 1 \;$

Cette équation diophantienne, qui intervient souvent dans l'étude des entiers de Dirichlet, correspond à l'expression, en termes de coordonnées, de la norme d'un entier de Dirichlet. La suite de l'article montre qu'elle est équivalente à une équation de Pell-Fermat.

Puissance du nombre d'or

Un exemple d'unité est donné par ω, on vérifie de fait que N(ω) = 0 + 0 - 1² = -1. La compatibilité de la norme avec la multiplication montre que si n est un entier relatif, ±ωⁿ est aussi une unité car :

$\mathcal N(\pm \omega^n) =\mathcal N(\omega^n)=\mathcal N(\omega)^n = (-1)^n \;$

Soit e un entier égal à 1 ou à -1 et n un entier relatif, eωⁿ est une unité de l'anneau des entiers de Dirichlet.

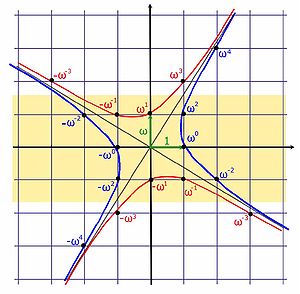
La figure de droite illustre le positionnement des unités, les branches bleues supportent les unités positives et les rouges, les négatives. Cette méthode, purement algébrique, pour déterminer les unités est généralisable. Brahmagupta l'avait remarqué, ce qui lui a permis de construire une méthode très générale sur ce principe, appelée méthode chakravala.

Une question plus délicate est celle de la réciproque, la réponse est donnée par la proposition suivante :

Soit ε un élément du groupe des unités, il existe un entier e égal à 1 ou -1 et un entier relatif n tel que ε soit égal à eωⁿ.

Cette question arrêta longuement les mathématiciens dans le cas général. C'est Joseph-Louis Lagrange qui finalement vient à bout^[7] du cas des entiers quadratiques en prolongeant les travaux d'Euler sur la fraction continue d'un nombre quadratique. Dirichlet trouve au siècle suivant une méthode de résolution valable pour tous les entiers algébriques, généralisant ainsi les travaux de Lagrange. Ce résultat est l'objet d'un théorème dit des unités de Dirichlet. Une démonstration simplifiée, pour résoudre uniquement le cas des entiers quadratiques, est proposé dans l'article Entier quadratique. Si l'objectif n'est que l'étude du groupe des unités des entiers de Dirichlet, une démonstration élémentaire est envisageable.

Démonstration

Soit ε = a + b.ω une unité de l'anneau. L'objectif est de montrer que, au signe près, ε est une puissance de ω. Si b est égal à 0 ou à 1, il existe exactement dix solutions qui se traitent manuellement. Ils correspondent aux dix solutions dans la bande orange de la figure.

Sinon, quatre cas se présentent, a et b positifs, a positif et b négatif, a négatif et b positif et enfin a et b négatif. Ces quatre cas correspondent aux huit branches asymptotiques des deux hyperboles de la figure qui se groupent deux à deux. Ils se traitent tous de manière analogue. Considérons donc le cas où a et b sont positifs et b est supérieur ou égal à deux.

Montrons que a < b < 2.a. Si b est plus petit ou égal à a alors N(a + b.ω) est plus grand que a² (et donc plus grand que 4), ce qui est impossible.

$\mathcal N(\epsilon) = a^2 + ab - b^2 = a^2 + b(a - b) \ge a^2 \ge 4\;$

Si b est plus grand que 2.a alors N(a + b.ω) est plus petit que -a², ce qui est tout aussi impossible.

$-\mathcal N(\epsilon) = b^2 - ab - a^2 = b(b - a) - a^2 \ge 2a^2 - a^2 \ge a^2 \ge 4\;$

Donc (a + b.ω).ω ^-1 = a₁ + b₁ω est aussi un élément du groupe de l'unité du même quadrant. En effet b₁ est égal à a et a₁ à b - a. Les deux coefficients sont strictement positifs et b₁ strictement plus petit que b. En réitérant le processus de multiplication par ω ^-1, on obtient finalement un élément du groupe de l'unité dont le coefficient de ω est soit zéro soit un. Un tel élément est égal à une puissance de ω à un facteur ±1. Ceci montre que ε est bien une puissance de ω.

Suite de Fibonacci

Article détaillé : Suite de Fibonacci.

Si l'on considère la suite des coordonnées de ωⁿ pour n un entier naturel, on obtient (1,0), (0,1), (1,1), (1,2), (2,3) ... On reconnait là une suite de Fibonacci :

Soit (a_n) une suite à valeur dans les entiers naturels définie par la relation de récurrence suivante :

$a_0 = 1,\;a_1 = 0 \quad\text{et}\quad \forall n \in \mathbb N \quad a_{n+2}= a_{n+1} + a_n \quad \text{alors}\quad \omega^n = a_n + a_{n+1}\omega \quad\text{et}\quad \omega^{-n} = (-1)^n(a_{n+2} -a_{n+1}\omega)$

Cette proposition se démontre par récurrence, un rapide calcul montre que la formule est vraie si n est égal à 0 ou 1, supposons la première formule vraie jusqu'à n :

$\omega^{n+1}= \omega\cdot\omega^n= \omega\cdot(a_n + a_{n+1}\omega) = a_n\omega + a_{n+1}\omega^2 = a_n\omega + a_{n+1}(1 + \omega) =a_{n+1} + (a_{n+1} + a_n)\omega\;$

Une démonstration de même nature établit la relation de récurrence pour les valeurs négatives de n.

Division euclidienne

Article détaillé : Anneau euclidien.

Existence

La norme possède une propriété importante, elle permet de définir une division euclidienne. Cette norme n'est pas toujours positive. Le stathme v, c’est-à-dire la fonction permettant de définir la division et égale à la valeur absolue dans le cas des entiers relatifs, ne doit prendre que des valeurs positives. Pour cette raison, on le choisit égal la valeur absolue de la norme. Cette application est encore multiplicative, c’est-à-dire que si α et β sont deux entiers de Dirichlet, alors : v(α.β) = v(α).v(β).

Soit α et β deux entiers de Dirichlet tel que β soit non nul, il existe un couple d'entiers de Dirichlet (θ,ρ) tel que :

$\alpha=\beta.\theta+\rho\quad avec \quad |\mathcal N(\rho)|<|\mathcal N(\beta)|\;$

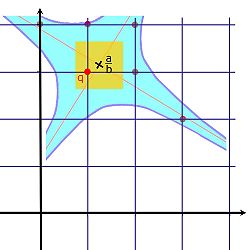
La démonstration est analogue à celle des entiers de Gauss. Considérons la fraction rationnelle α/β et l'ensemble des éléments ζ de Q[ $\sqrt 5$ ] tel que |N(α/β - ζ)| soit strictement inférieur à un. Cet ensemble correspond à la zone bleue de la figure de droite, délimitée par les quatre branches des hyperboles. L'intersection de cette zone avec les entiers de Dirichlet, correspondant aux points du réseau, sont les candidats à être les quotients de la division euclidienne. Ces candidats sont illustrés par un petit cercle sur la figure. Le carré, illustré en orange, de côté 1 et de centre α/β est strictement inclus dans la zone bleue. Il contient au moins un point θ, illustré ici en rouge. Ce point θ vérifie :

$|\mathcal N\left( \frac{\alpha}{\beta}- \theta \right)| <1 \mbox{ et si } \rho=\beta\left(\frac{\alpha}{\beta}- \theta\right) \mbox{ alors } |\mathcal N(\rho)|=|\mathcal N \left(\beta.\left(\frac{\alpha}{\beta}- \theta\right)\right)| = |\mathcal N(\beta)\cdot \mathcal N\left(\frac{\alpha}{\beta}- \theta \right)|<|\mathcal N(\beta)|$

Ceci montre qu'il existe une division euclidienne dans l'anneau des entiers de Dirichlet. Elle possède un aspect un peu déroutant, il n'existe pas un reste possible, mais jusqu'à une infinité. Le nombre de restes possibles est en effet lié au groupe des unités, si ρ₁ et ρ₂ sont deux restes possibles, il existe une unité ε tel que ρ₂ = ερ₁. Cette situation est finalement la même que pour les entiers relatifs ou il existe parfois deux restes possibles (cf division euclidienne).

Conséquences

Comme cet anneau est euclidien, il est principal, l'identité de Bézout s'applique ainsi que le lemme d'Euclide et le théorème fondamental de l'arithmétique. L'article Entier de Gauss propose des démonstrations directement applicables au cas traité ici. Les démonstrations sont très proches de celles de l'arithmétique usuelle. Montrons-le, par exemple, pour le lemme d'Euclide. Il indique que si α, β et γ sont trois entiers de Dirichlet tels que α divise le produit β.γ et tel que α et β soient premiers entre eux, alors α divise γ. Avec ces hypothèses et l'identité de Bézout, comme α et β sont premiers entre eux, il existe deux entiers de Dirichlet ρ et θ tels que α.ρ + β.θ = 1, on multiplie membre à membre par γ, on obtient α.ρ.γ + β.θ.γ = γ. Comme β.γ est un multiple de α, il existe un entier de Dirichlet δ tel que β.γ soit égal à α.δ. En remplaçant β.γ par α.δ, on obtient α(ρ.γ + θ.δ) = γ, ce qui démontre la proposition.

Cette démonstration est, à la modification près sur le terme d'entier qui devient entier de Dirichlet, exactement la même que celle du cas des entiers relatifs. Cette logique, qu'Euler tente d'appliquer, nécessite l'existence d'une division euclidienne, ce que Gauss a compris.

Petit théorème de Fermat

Article détaillé : Petit théorème de Fermat.

Si l'analogie est profonde, elle doit néanmoins être maniée avec précaution. Le petit théorème de Fermat, l'un des piliers de l'arithmétique élémentaire, s'exprime par exemple de manière un peu différente :

Soient π un nombre premier de Dirichlet, α un nombre entier de Dirichlet qui n'est pas un multiple de π et n un entier strictement positif égal à la valeur absolue de la norme de π, alors α^n-1 - 1 est un multiple de π.

En utilisant le langage des congruences, on obtient l'égalité suivante, caractéristique du petit théorème de Fermat :

$\alpha^{n-1} \equiv 1 \mod \pi \;$

La démonstration proposée ici ne fait appel ni à la théorie des groupes ni aux techniques plus sophistiquées comme celle de l'anneau quotient ou des corps finis. Les démonstrations de l'article Entier quadratique, faisant usage d'outils plus puissants arrivent à des conclusions plus générales avec des démonstrations plus succinctes.

Démonstration

La démonstration est un peu plus longue que celle, plus usuelle, des entiers naturels. Les nombres premiers ne sont, dans le cas étudié ici, pas tous de même nature, comme le montre la proposition suivante. Le terme π désigne un nombre premier de Dirichlet :

Soit π est un élément de N, soit la norme de π est, en valeur absolue, un nombre premier dans l'ensemble N des entiers naturels :

Le raisonnement est le suivant, on suppose que |N(π)| n'est pas un nombre premier dans les entiers naturels et on montre que π est un nombre premier dans N.

L'entier naturel |N(π)| n'est pas premier dans N par hypothèse, il admet deux diviseurs n et m dans N, chacun différent de 1. Soit β un nombre premier de Dirichlet présent dans la décomposition en facteurs premiers de n. Il est en effet possible de considérer n comme un entier de Dirichlet. Soit γ un entier de Dirichlet tel que β.γ soit égal n. Ce nombre β divise N(α) c'est-à-dire le produit de α et de son conjugué. Comme β est premier, le lemme d'Euclide, appliqué dans Z[ω], montre que β divise soit α soit son conjugué. Comme α et son conjugué sont des nombres premiers de Dirichet, β est égal soit à α soit à son conjugué. La norme N(α) est égale au produit de α et de son conjugué, on en déduit que γ.n est égal à soit à α soit à son conjugué. Comme α et son conjugué sont premiers de Dirichlet et que m n'est pas une unité par hypothèse, γ est égal à 1.

Or β est un nombre premier de Dirichlet, donc β.γ = n est un nombre premier, c'est-à-dire divisible seulement par lui-même ou par 1, à un facteur unité près. L'entier n divise le produit de α et de son conjugué, il divise l'un des deux. Comme ces deux nombres sont premiers de Dirichlet, il est égal à l'un des deux, à un facteur unité près. Si π ou son conjugué est égal à n, à un facteur unité près, alors π, tout comme son conjugué sont égaux à n. Ceci montre que le nombre premier de Dirichlet π est élément de N. Comme π est premier de Dirichlet, il est aussi premier dans N, ce qui termine la démonstration.

Étudions, dans un premier temps, le cas d'un nombre premier de Dirichlet π dont la norme n est en valeur absolue un nombre premier dans les entiers naturels. Un exemple est donné par 3 + 2.ω. Il vérifie l'égalité :

$\mathcal N(3 + 2\omega) = 3^2 + 3\times 2 - 2^2 = 11\;$

Si deux entiers de Dirichlet ont un produit égal à 3 + 2.ω, le produit de leur norme est égal à 11. Comme 11 est un nombre premier dans N, une des normes est égale à ±1, ce qui montre que l'entier de Dirichlet associé est une unité et donc que 3 + 2.ω n'admet pas de diviseur propre.

Si π est un nombre premier dont la norme n est, en valeur absolue, un nombre premier dans N, alors le petit théorème de Fermat est vérifié :

Le raisonnement utilisé consiste à se ramener à un cas où la formulation usuelle du petit théorème de Fermat s'applique. Soient p₁, p₂, a et b les quatre entiers relatifs tels que π = p₁ + p₂.ω soit égal à π et a + b.ω à α. Les entiers relatifs p₂ et n sont premiers entre eux, sinon p₂ serait un multiple de n d'après la formule exprimant la norme d'un entier de Dirichlet, en fonction de ses coordonnées. L'identité de Bézout montre l'existence de deux entiers g et h tel que p₂.g + n.h = -b. On en déduit que α + g.π + h.n est un entier relatif. De plus n est égal à π.φ(π) donc :

$\alpha + \pi(g + h\varphi(\pi)) \in \mathbb Z$

Ce qui signifie que α est congru à un entier relatif modulo π. Notons c cet entier relatif, comme α est congru à c modulo π, α^n-1 est congru c^n-1 modulo π. Le petit théorème de Fermat permet d'affirmer que c^n-1 est congru à 1 modulo n donc α^n-1 est congru à 1 modulo n et donc aussi aux diviseurs de n comme π. Ce qui termine la démonstration.

Il reste le deuxième cas à traiter, celui où π est à la fois un nombre premier de Dirichlet et un entier naturel. L'entier π est aussi un nombre premier dans les entiers naturels. En effet, il n'admet pas de diviseur autre qu'une unité et lui-même, à un facteur unité près, dans les entiers de Dirichlet et donc a fortiori dans N. L'objectif est alors de montrer que pour tout α, non multiple de π, la congruence suivante est vérifiée :

$\alpha^{\pi^2 - 1} \equiv 1 \quad \mod \pi\;$

Si π est un nombre premier de N premier dans l'anneau des entiers de Dirichlet, alors α^{2π -1} est congru à 1 modulo π :

La configuration est suffisamment différente pour devoir reprendre pas à pas la démonstration du petit théorème de Fermat. Soit C l'ensemble des entiers non nuls de Dirichlet c + d.ω tel que les coordonnées c et d se situent dans l'intervalle [0, p-1]. L'ensemble C forme une espèce de carré et contient exactement π² - 1 points. Le -1 correspond au zéro que l'on a retranché de l'ensemble.

Un élément β de l'anneau des entiers de Dirichlet, non multiple de π, est congru à un et un seul élément de C modulo π.

On note β = a_β + b_β.ω. Les divisions euclidiennes dans l'ensemble des entiers relatifs (avec un reste toujours positif) de a_β et de b_β montrent qu'il existe un représentant de β dans C, en effet :

$\exists\, d_a, d_b, r_a, r_b \in \mathbb N \quad a_{\beta} = \pi d_a + r_a,\; b_{\beta} = \pi d_b + r_b \quad\text{avec}\; 0\le d_a < \pi,\; 0\le d_b < \pi\quad \text{et } \beta = r_a + r_b\omega + \pi(d_a + d_b\omega)$

On note β_c = r_a + r_b.ω, β_c est congru à β modulo π et est élément de C. Réciproquement, la différence entre deux éléments de C ne contient que des points aux coordonnées inférieures à π en valeur absolue, pour que cette différence soit un multiple de π, il faut qu'elle soit nulle. Ce qui montre l'unicité du représentant β_c de β dans C.

Soit ψ l'application de C dans C qui à β, un élément de C, associe le représentant de α.β dans C.

L'application ψ est une bijection.

Soit β₁ et β₂ deux éléments de C ayant même image par ψ. La différence ψ(β₁) - ψ(β₂) est nulle, ce qui signifie que α.(β₁ - β₂) est un multiple de π. Comme π est premier en tant qu'entier de Dirichlet, il divise soit α, soit β₁ - β₂. Par hypothèse π ne divise pas α, il divise donc β₁ - β₂. La proposition précédente montre que cela signifie que β₁ et β₂ sont égaux, c'est-à-dire que ψ est injective. Toute application injective d'un ensemble fini dans lui même est une surjection, le caractère bijectif de ψ est ainsi démontré.

On désigne par Π_c le produit de tous les éléments de C. Cette valeur est l'équivalent du terme (π-1)! dans la démonstration élémentaire de l'article Petit théorème de Fermat.

L'entier de Dirichlet Π_c.α^π²-1 est congru à Π_c modulo π.

Il suffit de remarquer que Π_c est le produit d'exactement les π² - 1 éléments de C. Comme ψ est une bijection il correspond aussi au produit des π² - 1 éléments ψ(β) si β décrit C. Or ce produit est congru à Π_c.α^π²-1 modulo π car dans le monde des congruences, ψ correspond à une multiplication par α. Ceci montre que Π_c.α^π²-1 est congru à Π_c modulo π.

Conclusion

Le paragraphe précédent montre que Π_c(α^π²-1 - 1) est un multiple de π. Aucun élément constituant le produit Π_c n'est un multiple de π, la contraposée du lemme d'Euclide permet de conclure que π ne divise pas Π_c. Si π ne divise par Π_c une nouvelle application de ce même lemme montre que π divise l'autre facteur : α^p²-1 - 1. Dire que π divise α^π²-1 - 1 est exactement équivalent au petit théorème de Fermat, la démonstration est ainsi achevée.

Nombres premiers

Définitions et exemples

Un peu de vocabulaire est utile :

Un nombre premier p dans l'ensemble des entiers naturels est dit inerte si et seulement si, il est premier en tant qu'entier de Dirichlet.

Un entier de Dirichlet α est dit irréductible si et seulement si, il existe une unité ε et un nombre premier de Dirichlet π tel que α soit égal à ε.π.

Autrement dit, un entier de Dirichlet est dit irréductible s'il est différent d'une unité et s'il n'admet comme diviseur que lui-même et 1 à un facteur unité près.

Un nombre premier p dans l'ensemble des entiers naturels est dit décomposé si et seulement si, il n'est pas irréductible en tant qu'entier de Dirichlet.

L'entier $\sqrt 5$ est un entier de Dirichlet irréductible. On remarque en effet que la norme de $\sqrt 5$ est égale à -5, dont la valeur absolue est un nombre premier dans les entiers naturels. On dispose en effet de la propriété suivante :

Un entier de Dirichlet ayant une norme en valeur absolue égale à un nombre premier est irréductible.

La valeur 2 est un nombre premier de Dirichlet, même si sa norme n'est pas irréductible. Il suffit pour cela de montrer qu'il n'existe pas d'entier de Dirichlet dont la norme est égale à deux. Tout diviseur de deux possède pour norme égale en valeur absolue soit à 1 soit à 4 (c’est-à-dire la norme de deux). Montrons, par l'absurde qu'il n'existe pas d'entier de Dirichlet de norme égal à ±2. Supposons qu'un tel nombre existe et soit a et b les deux entiers relatifs de même parité tel que 1/2(a + b. $\sqrt 5$ ) soit égal à ce nombre. Sa norme est égale à deux, donc a² + 5.b² = ±8. Si a et b sont pairs, alors il existe deux entiers u et v tel que a = 2.u et b = 2.v, l'équation devient u² + 5.v² = ±2, une analyse modulo quatre montre que le premier terme ne peut jamais être congru à deux, d'où une contradiction si a et b sont pairs. Si a et b sont impairs, alors il existe u et v tel que a = 2.u + 1 et b = 2.v + 1, l'équation devient en simplifiant par 4 : u.(u + 1) - 5.v.(v+ 1) - 1 = ±2, le premier terme est impair le second pair, d'où une contradiction si a et b sont impairs.

Des raisonnements de cette nature permettent de trancher au cas par cas pour savoir si un entier de Dirichlet est irréductible ou non. Une méthode plus générale est nécessaire pour établir la géographie des nombres premiers.

Résidu quadratique

La démonstration du petit théorème de Fermat établit des différences de nature entre les nombres premiers de N. Certains sont cassés dans l'arithmétique de Dirichlet, d'autres non. Pour établir la géographie des nombres premiers de Dirichlet, il est nécessaire de savoir lesquels résistent ainsi que ceux qui se brisent. Cette question est liée à l'équation diophantienne suivante, si p désigne un nombre premier de N :

$(1) \quad x^2 - p\cdot y = 5\;$

Elle fut résolue dans le cas général par Gauss qui appela le théorème associé, théorème d'or. Il est maintenant plus connu sous le nom de Loi de réciprocité quadratique. Résoudre cette équation revient à déterminer si 5 est ou non le reste d'une division euclidienne d'un carré parfait par p, un nombre premier. On dit alors que 5 est un résidu quadratique modulo p. Le petit théorème de Fermat permet de montrer que :

Le nombre 5 est le reste d'une division euclidienne d'un carré parfait par un nombre premier p différent de 5 si et seulement si p est congru à ±1 modulo 5.

La relation entre l'équation (1) et la nature des nombres premiers est donnée par la proposition suivante :

Un nombre premier p de N différent de 2 est inerte, si et seulement si, 5 n'est pas un résidu quadratique modulo p.

Résoudre cette équation permet d'établir des résultats un peu inattendus, connu sous le nom de Loi d'apparition des nombres premiers au sein de la suite Fibonacci. Si (a_n) désigne la suite de Fibonacci :

Si p est un nombre premier de N différent de 5 et décomposé, alors a_p est un multiple de p ainsi que a_p-1 - 1.

Les démonstrations se fondent sur les propriétés géométriques du nombre d'or ainsi que le petit théorème de Fermat. Une propriété du nombre d'or est d'intervenir dans la construction à la règle et au compas du pentagone régulier. Si les sommets du polygone sont vus comme des points du plan complexe, ils sont racines du polynôme X⁵ - 1 = 0. Le petit théorème de Fermat indique lui que, dans le monde des congruences modulo π, tout résidu est solution de l'équation X^p²-1 - 1 ≡ 0 mod p, si p désigne la valeur absolue de la norme de π. L'analogie est suffisante. La preuve se résume à montrer qu'un nombre premier p différent de 5 n'est pas irréductible dans les entiers de Dirichlet si et seulement si, p² - 1 est un multiple de 5.

Une fois encore, l'usage d'outils sophistiqués permet des démonstrations plus rapides pour des résultats plus généraux. Ici, l'outil clé est la loi de réciprocité quadratique. Elle se démontre, par exemple avec les corps finis ou les groupes abéliens finis et particulièrement leur analyse harmonique. Les démonstrations proposées ici se cantonnent aux outils de l'arithmétique élémentaire.

Démonstrations

Montrons dans un premier temps l'équivalence entre l'existence d'une solution à l'équation diophantienne et le fait que p soit décomposé.

Un nombre premier p de N différent de 2 est inerte, si et seulement si, 5 n'est pas un résidu quadratique modulo p :

Traitons tout d'abord le cas où p est égal à 5. Il n'est pas premier dans Z[ω] car

\sqrt 5

le divise et il est bien un résidu quadratique car 0² et 5 ont même reste par la division euclidienne par 5.

Le principe de la démonstration pour les autres cas se fonde sur une propriété établie pour prouver le petit théorème de Fermat. Un nombre premier p est inerte si et seulement si ω n'est congru à aucun entier compris entre 0 et p - 1 modulo π, ici π désigne un facteur premier de p. Si p est premier, π et p sont confondus à un facteur unité près, sinon π divise strictement p. Si p n'est pas premier, tout entier de Dirichlet est congru à un entier compris entre 0 et p - 1 modulo π (cf paragraphe précédent). En revanche, si p est premier, aucun point a + b.ω avec a compris 0 entre p - 1 et b compris entre 1 et p - 1 n'est congru à un entier compris entre 0 et p - 1 modulo p et donc modulo π.

Supposons que ω soit congru à un entier w modulo π et montrons que 5 est un résidu quadratique modulo p. Le nombre 4(ω² - ω - 1) est égal à 0, donc 4w² - 4w - 4 congru à 0 modulo π ou encore, est un multiple de π. Ceci montre que 4w² - 4w + 1 - 5, égal à (2w - 1)² - 5, est un multiple de π, en conséquence (2w - 1)² est un carré parfait congru à 5 modulo π. Le conjugué de (2w - 1)² - 5, égal à lui même est un multiple de φ(π). La décomposition en facteurs premiers de (2w - 1)² - 5 contient à la fois π et φ(π), ce qui permet de conclure que (2w - 1)² - 5 est un multiple de p dans Z[ω]. Il existe un entier de Dirichlet q tel que p.q est égal à (2w - 1)² - 5. Comme (2w - 1)² - 5 et p sont entiers relatifs, q l'est nécessairement. On a montré l'existence d'un carré parfait c² tel que c² - 5 est un multiple de p dans N, 5 est bien un résidu quadratique modulo p.

Réciproquement, supposons que c soit un résidu quadratique de 5 modulo p et montrons que ω est congru à un entier modulo π. L'identité de Bézout montre l'existence d'un entier d tel que 2.d est congru à 1 modulo π car π est premier de Dirichlet, 2 et π sont premiers entre eux. L'entier 2.d(1 + c) vu comme un entier de Dirichlet est congru à 2.ω modulo π et donc l'entier d(1 + c) est congru à ω. La division euclidienne de d(1 + c) par p montre l'existence un entier naturel compris entre 0 et p - 1 congru à d(1 + c) modulo p et donc modulo π. Le fait que ω soit congru à un entier compris entre 0 et p - 1 modulo π montre que p n'est pas irréductible et termine la démonstration.

Etudions le cas simple, c'est-à-dire celui où p est congru à 2 ou à 3 modulo 5. Un rapide calcul montre que p n'est pas décomposable.

Soit p un nombre premier de N. Si p est congru à 2 ou à 3 modulo 5, p est inerte et 5 n'est pas un résidu quadratique modulo p :

Supposons que p soit un nombre premier décomposable, il existe un entier de Dirichlet a + b.ω de norme égale à p. Cette norme est égale à a² + a.b - b², calculons sa congruence modulo 5 :

$\pm p = a^2 +ab - b^2 \equiv a^2 + 2a3b + 9b^2 -10b^2 \equiv (a+3b)^2 \mod 5\;$

Un carré parfait modulo 5 n'est jamais congru à 2 ou à 3, en conséquence, si p est n'est pas décomposable s'il est congru à 2 ou à 3 modulo 5. La proposition précédente montre qu'alors 5 n'est pas un résidu quadratique.

L'étape d'après consiste à utiliser la propriété géométrique du nombre d'or. Un pentagone se définit aussi comme les racines du polynôme cyclotomique X⁵ - 1. Une méthode relativement simple pour une équation d'un degré aussi élevé permet de venir à bout de l'extraction de racine. La première étape voit l'apparition d'une valeur formellement proche du nombre d'or, ce qui permet d'établir la proposition suivante :

Soit p un nombre premier de N différent de 2 et de 5 et π un nombre premier divisant p. S'il existe un entier de Dirichlet α non congru à 1 modulo π tel que α⁵ - 1 soit un multiple de π, alors l'entier p est décomposé :

Pour la démonstration, on utilise l'égalité suivante :

$\alpha^5 - 1 = (\alpha - 1)(1 + \alpha + \alpha^2 + \alpha^3 + \alpha^4)\;$

Supposons que α⁵ - 1 soit multiple de π et montrons que p est décomposable dans les entiers de Dirichlet. Le lemme d'Euclide assure que l'un des deux facteurs de l'égalité précédente est un multiple de π. Par hypothèse, ce n'est pas le premier, c'est donc le dernier. On obtient :

$1 + \alpha + \alpha^2 + \alpha^3 + \alpha^4 \equiv 0 \mod \pi \quad\text{et}\quad \alpha + \alpha^2 + \alpha^3 + \alpha^4 \equiv -1 \mod \pi\;$

En multipliant la première égalité par α on remarque que α⁵ est congru à -α - α² - α³ - α⁴ donc à 1 modulo π d'après la deuxième égalité. Si u désigne α + α⁴ et v α² + α³, comme α⁵ est congru à 1 modulo π :

$u + v \equiv - 1 \mod \pi \quad\text{et}\quad u\cdot v=(\alpha + \alpha^4)(\alpha^2 + \alpha^3)=\alpha^3 + \alpha^4 + \alpha + \alpha^2 \equiv - 1\mod \pi \;$

En multipliant u + v par u :

$u(u+v) + u \equiv 0 \mod \pi,\quad u^2 + u - 1 \equiv 0 \mod \pi,\quad 4u^2 + 4u - 4 = (u + 1)^2 - 5 \equiv 0 \mod \pi\;$

Il existe un entier congru à 5 modulo π ce même entier est aussi congru à φ(π) donc au produit car ces deux entiers de Dirichlet sont premiers et 5 est congru à un carré parfait modulo p. Le fait que 5 soit un résidu quadratique ainsi que la proposition précédente, permet de conclure.

Il est temps d'utiliser le petit théorème de Fermat, si p est irréductible l'exposant du petit théorème de Fermat est égal à p² - 1 un multiple de 5 si p est congru à 1 ou à 4 modulo 5. Le petit théorème de Fermat traite d'un polynôme multiple de X⁵ - 1, l'aide de la proposition précédente permet de conclure.

Si p est un nombre premier congru à 1 ou à 4 modulo 5, p est décomposé :

Raisonnons par l'absurde et supposons que p soit congru à 1 ou à 4 modulo p et irréductible dans les entiers de Dirichlet. Un simple calcul montre que p² - 1 est un multiple de 5. On note k l'entier tel que 5.k est égal p² - 1. Soit α un entier de Dirichlet non multiple de p et n le plus petit entier tel que αⁿ - 1 soit un multiple de p. Le petit théorème de Fermat nous indique que n est un diviseur de p² - 1. La proposition précédente montre que n n'est pas un multiple de 5, sinon α^n/5 serait un entier non congru à 1 modulo p tel que, à la puissance 5, il serait congru à 1 modulo p. L'existence d'un tel entier montre que 5 est un résidu quadratique modulo p et que p est décomposable. On en déduit que n est un diviseur de k. Ceci montre que pour tout entier de Dirichlet α non multiple de p, α^k - 1 est un multiple de p.

Soient k entiers de Dirichlet α₁, α₂, ..., α_k non multiple de p et tous de congruences différentes modulo p. Il en existe toujours, le paragraphe précédent montre qu'il existe exactement p² - 1 congruences différentes modulo p et k est strictement plus petit que p² - 1. Le polynôme X^k - 1 annule la congruence de α₁, ce qui montre l'existence d'un polynôme P₁(X) de degré k - 1 tel que :

$X^k - 1 \equiv (X - \alpha_1)P_1(X) \mod p\;$

L'entier de Dirichlet α₂^k - 1 est un multiple de p, donc (α₁ - α₂)P₁(α₂) est aussi un multiple de p. Par construction des α_j, α₁ - α₂ n'est pas un multiple de p. Le lemme d'Euclide montre que P₁(α₂) est un multiple de p. Ceci montre l'existence d'un polynôme P₂(X) tel que :

$P_2(X) \equiv (X - \alpha_2)P_1(X) \mod p \quad\text{et}\quad X^k - 1 \equiv (X - \alpha_1)(X - \alpha_2)P_2(X) \mod p \;$

En continuant le même raisonnement jusqu'à k on obtient la congruence :

$X^k - 1 \equiv (X - \alpha_1)(X - \alpha_2) \cdots (X - \alpha_k) \mod p \;$

Considérons alors un entier de Dirichlet α non multiple de p et congru à aucun des éléments α₁, α₂, ..., α_k. On a vu que α^k - 1 est un multiple de p, donc :

$(\alpha - \alpha_1)(\alpha - \alpha_2) \cdots (\alpha - \alpha_k) \equiv 0 \mod p \;$

Le terme précédent est un multiple de p, pourtant aucun des facteurs α - α_j n'est un multiple de k. Cette assertion contredit le lemme d'Euclide et ne peut être juste. En conséquence l'hypothèse p est irréductible dans les entiers de Dirichlet est fausse, ce qui démontre la proposition.

Si p est un nombre premier de N différent de 5 et décomposé, alors a_p est un multiple de p ainsi que a_p-1 - 1 :

La démonstration est rapide avec le petit théorème de Fermat. Le nombre p admet d'après les deux propositions précédentes deux nombre premiers π et φ(π) dans sa décomposition en facteurs premiers. La norme de chacun des nombres premiers de Dirichlet est p. Le petit théorème de Fermat affirme que ω^p-1 - 1 est un multiple de π et de φ(π) donc de p. L'analyse de la suite de Fibonacci montre que ω^p-1 - 1 = a_p-1 - 1 + a_p.ω, ce qui démontre le résultat. Une vérification manuelle montre que a₁₁ est égal à 55, a₁₀ à 33 + 1, a₁₉ à 2585 = 19x136 et a₁₈ à 19x84 + 1.

Equation de Pell-Fermat

Article détaillé : Équation de Pell-Fermat.

Équation

L'objectif est de résoudre l'équation suivante :

$(1)\quad x^2 -5 y^2 = d \quad\text{avec}\quad d \in \mathbb Z -\{0\}\;$

Dans un premier temps, l'objectif est de se ramener à une équation utilisant l'expression de la norme dans l'anneau des entiers de Dirichlet. Un changement de variable permet d'écrire la solution de la manière suivante :

$x = u + \frac v2,\; y = \frac v2 \quad\text{alors}\quad (2)\quad u^2 + u\cdot v - v^2 = d \;$

Pour une raison de simplicité, on appelle solution de l'équation (2) tout entier de Dirichlet de norme égale à d. En effet, dire qu'un entier de Dirichlet a + b.ω est de norme d revient à dire que a² + a.b - b² = d. Cette remarque, ainsi que la connaissance de la structure des nombres premiers de Dirichlet permet de venir à bout de l'équation (1).

Le facteur 1/2, introduit par le changement de variables, doit être pris en compte. Une proposition intermédiaire est nécessaire :

S'il existe un entier de Dirichlet de norme égale à d en valeur absolue, alors il existe un entier de Dirichlet de la forme a + 2b.ω de norme d en valeur absolue et le couple (a - b, b) est une solution de l'équation (1) pour le paramètre ±d. Ici a et b désigne deux entiers relatifs.

Soit a₁ + b₁.ω un entier de Dirichlet de norme égale à d en valeur absolue. Si b₁ est pair la proposition est bien vérifiée. Sinon, deux cas se présentent, selon la parité de a₁. Si a₁ est impair, on remarque que ω est une unité, donc ω.(a₁ + b₁.ω) est de norme égale à d en valeur absolue. L'égalité ω.(a₁ + b₁.ω) = b₁ + (a₁ + b₁).ω et le fait que a₁ et b₁ soient impairs permet de conclure. Si a₁ est pair, appliquons le même raisonnement avec 1 + ω, on obtient l'égalité suivante : (1 + ω).(a₁ + b₁).ω = a₁ + b₁ + (a₁ + 2b₁).ω. Cette dernière égalité, ainsi que le fait que a₁ soit pair permet encore de conclure. Pour terminer la démonstration, il suffit de remarquer que le couple (a - b, b) est effectivement une solution de l'équation (1).

Enfin si (a, b) est une solution, alors (±a, ±b) est aussi une solution. Pour cette raison, ne sont cherchées uniquement les solutions tel que a et b sont positifs.

La valeur absolue de d est égale à un

Résoudre l'équation (2) dans le cas où le paramètre est égal à ±1 est possible avec la connaissance du groupe des unités. Toutes les unités sont connues, elles sont de la forme ±ωⁿ où n est un entier relatif et le signe de la norme est celui de (-1)ⁿ. Enfin, la suite de Fibonacci donne les coordonnées exactes des unités.

En revanche, les solutions recherchées sont celles qui ont pour coefficients b un entier pair. Une récurrence permet d'établir que, si (a_n) désigne la suite de Fibonacci déjà utilisée, a_n est pair si et seulement si n est congru à 1 modulo 3. L'article Entier algébrique étudie cette configuration pour toutes les équations de Pell-Fermat. Cela permet de conclure que :

L'ensemble des solutions S₁ de l'équation (1) pour le paramètre d égal à 1 est :

$S_1 = S_{1+}\cup S_{1-} \quad\text{avec}\quad \begin{align} S_{1+} & = \left\{(a,b) \in \mathbb Z^2,\; a = a_{6k} + \frac {a_{6k+1}}2 ,\; b = \frac {a_{6k+1}}2 ,\quad k \in \mathbb N \right\} \\ S_{1-} & = \left\{(a,b) \in \mathbb Z^2,\; a = a_{6k+2} - \frac {a_{6k+1}}2 ,\; b = \frac {a_{6k+1}}2 ,\quad k \in \mathbb N \right\} \end{align}$

L'ensemble des solutions S_-1 de l'équation (1) pour le paramètre d égal à -1 est :

$S_{-1} = S_{-1+}\cup S_{-1-} \quad\text{avec}\quad \begin{align} S_{-1+} & = \left\{(a,b) \in \mathbb Z^2,\; a = a_{6k+3} + \frac {a_{6k+4}}2 ,\; b = \frac {a_{6k+4}}2 ,\quad k \in \mathbb N \right\} \\ S_{-1-} & = \left\{(a,b) \in \mathbb Z^2,\; a = a_{6k+5} - \frac {a_{6k+4}}2 ,\; b = \frac {a_{6k+4}}2 ,\quad k \in \mathbb N \right\} \end{align}$

La valeur absolue de d est égale à un nombre premier p

L'analyse des nombres premiers de Dirichlet permet de résoudre la question. La lettre p désigne ici un entier naturel premier.

Si p est congru à 2 ou à 3 modulo 5, alors l'équation (1) n'admet pas de solution pour le paramètre ±p.

En effet, L'équation (2) n'a pas de solution car il n'existe aucune norme dans Z[ω] égale à ±p et toute solution de l'équation (1) se construit à l'aide d'une solution de l'équation (2).

Si p est congru à 1 ou à 4 modulo 5, alors l'équation (1) admet une infinité de solutions pour les deux paramètres p et -p.

Si p est congru à 1 ou à 4, il existe un nombre premier π ayant pour norme p. Quitte à multiplier π par ω ou ω², il est possible de construire une solution (a, b) à de l'équation (2) tel que b soit pair. Multiplier cette solution par les éléments de S₁ d'un côté et par S_-1 de l'autre fournit une infinité de solutions pour chacun des deux paramètres p et -p. L'article équation de Pell-Fermat montre qu'il n'y en a pas d'autres.

Cas général

Le cas général est analogue à celui des équations de type x² ± n.y² = d, il est traité en détail dans l'article Théorème des deux carrés de Fermat. Il prend la forme suivante :

S'il existe un exposant d'un entier naturel premier congru à 2 ou à 3 modulo 5 dans la décomposition en facteurs premiers de d alors l'équation (1) n'a pas de solution.

On raisonne par contraposé, c'est-à-dire que l'on suppose que l'équation (1) admet une solution pour d et on montre que les exposants des facteurs premiers de d congru à 2 ou 3 modulo 5 sont pairs.

Soit (a, b) une solution de l'équation (1), α = a - 2b + 2b.ω est de norme d. Considérons la décomposition en facteurs premiers de Dirichlet de α. Le paragraphe précédent montre que la norme d'un nombre premier de Dirichlet est, soit en valeur absolue égale au carré d'un entier naturel premier congru à 2 ou à 3 modulo 5, soit à un entier naturel premier congru à 1 ou à 4 modulo 5 ou encore à 5. L'exposant des facteurs premiers de la norme de α congru à 2 ou à 3 est en conséquence toujours pair car la décomposition en facteurs premiers est unique. On en déduit que la décomposition en facteurs premiers de d ne contient pas d'exposant impair pour les facteurs premiers congru à 2 ou à 3 modulo 5. Ce qui termine la démonstration.

Si d ne contient aucun exposant impair pour les entiers naturels premiers congru à 2 ou à 3 modulo 5 présents dans sa décomposition en facteurs premiers, alors l'équation (1) admet une solution pour les deux paramètres d et -d.

Si d vérifie l'hypothèse de la proposition, il existe une suite finie de nombres premiers p_i congru à 2 ou à 3 modulo 5, une suite de nombres premiers (q _j) non congru à 2 ou à 3 modulo 5 et deux suites à valeur dans les entiers strictement positifs (n_i) et (m_j) telles que :

$|d| = \prod_{i,j} p_i^{2n_i}q_j^{m_j}\;$

L'analyse des nombres premiers de Dirichlet montre l'existence d'entiers α_j tels que leurs normes vérifient les égalités suivantes :

$\forall j\quad |N(\alpha_j)|=q_j \quad\text{et si}\quad \alpha = \prod_{i,j} p_i^{n_i} \alpha_j^{m_j},\quad N(\alpha) = \pm d \;$

A partir de là, on raisonne comme pour le cas où d est premier et on construit deux suites infinies de solutions, une pour la valeur d et l'autre pour la valeur -d. On remarque qu'il existe deux solutions différentes pour une norme égale à q _j, soit α_j² soit q _j. La combinatoire de toutes les écritures d'un nombre de norme d, donne l'intégralité des solutions, une fois composées avec les ensembles S₁ et S_-1.

Propriété associée à la démonstration du dernier théorème de Fermat

Article détaillé : Démonstrations du dernier théorème de Fermat.

Dirichlet s'est intéressé à cet anneau d'entiers dans un but particulier: résoudre l'équation de Fermat dans le cas où le paramètre est égal à cinq. Cette résolution revient à montrer qu'il existe pas de triplet (x, y, z) tel que x.y.z soit différent de zéro et x⁵ + y⁵ = z⁵.

Cette résolution se fonde sur un lemme technique. La démonstration de ce lemme est la cause originale de l'étude par Dirichlet de cet anneau d'entier :

Soit a et b deux entiers relatifs différents de zéro, premiers entre eux, de parités différentes, tel que cinq divise b et a² - 5.b² soit une puissance cinquième. Alors il existe deux entiers différents de zéro c et d premiers entre eux, de parités différentes tel que cinq ne divise pas c et :

$a=c(c^4+50c^2d^2+125d^4)\quad et \quad b=5d(c^4+10c^2d^2+5d^4)\;$

Démonstration

1. il existe quatre entiers relatifs m, n, t, u tel que a + b. $\sqrt 5$ = 1/2.(t + u. $\sqrt 5$ ).[1/2.(m + n. $\sqrt 5$ )] ⁵ où 1/2.(t + u. $\sqrt 5$ ) est une unité et 1/2.(m + n. $\sqrt 5$ ) est un entier de Dirichlet (donc m et n ont même parité).

a² - 5.b² est le produit de a + b.

\sqrt 5

et de son conjugué. Si a + b.

\sqrt 5

est premier avec son conjugué, alors il est le produit d'une puissance cinquième et d'une unité car l'anneau de Dirichlet est euclidien donc factoriel.

Soit d un entier de Dirichlet premier ou une unité, divisant a + b.

\sqrt 5

et son conjugué, il existe alors e et f deux entiers de Dirichlet tel que:

$d.e=a+\sqrt{5}.b\; , \; d.f=a-\sqrt{5}.b\; , \; d.(e+f)=2.a \; et \; d.(e-f)=2.\sqrt{5}.b\;$

Si d divise

\sqrt 5

, comme

\sqrt 5

est premier dans les entiers de Dirichlet, d est égal à

\sqrt 5

à une unité près. Comme 2 est aussi premier dans les entiers de Dirichlet,

\sqrt 5

divise a et 5 divise a² et donc a. 0r 5 divise b, de plus a et b sont premiers entre eux. Donc 5 ne peut diviser a et par voie de conséquence

\sqrt 5

ne divise pas d.

2 ne peux pas diviser d car alors deux divise a + b.

\sqrt 5

et a/2 +

\sqrt 5

.b/2 serait élément des entiers de Dirichlet, ce qui est incompatible avec le fait que a et b sont de parités différentes. En conséquence, d divise a et b. Le conjugué de d divise aussi a et b car ils sont entiers relatifs, et le produit de d et de son conjugué divise aussi a et b car d et son conjugué sont premiers entre eux (d est soit premier soit une unité). Ce produit est un entier, il est donc égal à ±1. En conclusion, les seuls entiers de Dirichlet qui divisent a + b.

\sqrt 5

et son conjugué sont des unités, la première remarque permet alors de conclure et :

$a+\sqrt{5}.b= \frac{1}{2}.(t + \sqrt {5}.u).\left( \frac{1}{2}(m + \sqrt{5}.n)\right)^5\;$

2. Il est possible de choisir m et n tel que t soit égal à 1 et u à 0.

Notons 1/2.(α +

\sqrt 5

.β) = [1/2.(m +

\sqrt 5

.n)]⁵. Montrons que β est un multiple de cinq et que α ne l'est pas. L'égalité s'écrit en développant l'égalité avec la formule du binôme :

$16.(\alpha+\sqrt{5}.\beta)=(m+\sqrt{5}.n)^5=m^5+10.5.m^3.n^2+5.25.m.n^4+\sqrt{5}.(5.m^4.n + 10.5.m^2.n^3+25.n^5) \;$

β apparaît clairement comme un multiple de cinq, si α l'est, alors a + b.

\sqrt 5

l'est aussi et comme b l'est, a l'est aussi. Or a n'est pas un multiple de cinq car b l'est et a et b sont premiers entre eux (dans l'ensemble des entiers relatifs).

Montrons alors que u est aussi un multiple de cinq :

$4.(a+\sqrt{5}.b)=(t + \sqrt {5}.u).(\alpha+\sqrt{5}.\beta)=t.\alpha + 5.u.\beta + \sqrt{5}.(t.\beta + u.\alpha) \quad et \quad u.\alpha = 4.b -t.\beta\;$

Cinq est multiple de b et de β, donc α.u est multiple de cinq. comme α n'est pas multiple de cinq, u l'est.

Montrons que t + u.

\sqrt 5

est une puissance cinquième. Tout élément du groupe de l'unité est une puissance positive soit de ω, soit de -ω, soit de $\scriptstyle {\bar {\omega}}$ soit de - $\scriptstyle {\bar {\omega}}$ et donc :

$\exists \epsilon, \epsilon' \in \{-1, 1\}\; et\;n\in \mathbb{N} \; \mbox{ tel que } 2^{n-1}.(t + \sqrt{5}.u)=\epsilon(1+\epsilon'. \sqrt{5})^n\;$

Une nouvelle utilisation de la formule du binôme montre l'égalité suivante et le fait que n est un multiple de cinq:

$n + \sum_{i=2}^{\frac{n}{2} + 1} {n \choose {2.i - 1}}.5^{i-1}=\epsilon'.\epsilon.2^{n-1}.u$

Comme n est une puissance de cinq il existe une unité θ tel que t +

\sqrt 5

.u = θ⁵. En conclusion [θ.(m +

\sqrt 5

.n)]⁵ est égal à a +

\sqrt 5

.b. Ce qui revient à dire que l'unité peut être choisie égale à 1.

3. m et n sont pairs.

La formule du binôme montre, en développant l'égalité a +

\sqrt 5

.b = (m +

\sqrt 5

.n)⁵ :

$32.a=m(m^4+50.m^2.n^2+125.n^4)\quad et \quad 32.b=5.n.(m^4 + 10m^2.n^2+5.n^4) \;$

Supposons que m et n soient impairs, alors m⁴ + 10.m².n² + 5.n⁴ est congru à 0 modulo 32 car ni 5 ni n ne sont pairs. Les puissances quatrièmes de nombres impairs ne sont congrus qu'à 1 ou à 17 modulo 32. Il existe donc quatre cas à étudier. Considérons le premier cas : n et m ont une puissance de 4 congru à 1 modulo 32. Leurs carrés sont congrus soit à 1 soit à 17, et le produit de leurs carrés est alors congru soit à 1 soit à 17. L'expression est alors congru soit à 7 soit à 23. En conséquence, n et m ne peuvent posséder tout deux une puissance de 4 congru à 1 modulo 32 car l'expression doit être congru à 0. L'analyse des trois autres cas est analogue et tout aussi impossible. On en conclut que m et n sont nécessairement pairs.

4. Fin de la démonstration.

Alors l'égalité s'écrit a + b.

\sqrt 5

= (c + d.

\sqrt 5

) ⁵ où 2.c = m et 2.d = n. En choisissant le signe de c (respectivement d)comme égal à celui de a (respectivement b) on obtient :

$a= c.(c^4+50.c^2.d^2+125.d^4)\quad et \quad b= 5.d(c^4 + 10.c^2.d^2+5.d^4) \;$

Si c ou d sont nuls, alors soit a soit b est nul, ce qui n'est pas le cas donc c et d sont tous deux non nuls. Tout diviseur commun à c et à d est diviseur commun à a et à b, donc c et d sont premiers entre eux car a et b le sont. Si c et d sont de même parité, alors a et b sont tous les deux pairs, ce qui n'est pas le cas, donc c et d sont de parités différentes. Cinq divise b donc il ne divise pas a et donc il ne divise pas c.

Voir aussi

Notes

↑ Si le contenu mathématique de l'article fait partie du corpus usuel de la théorie des nombres, le terme entier de Dirichlet n'est pas commun. L'ensemble des entiers de cette nature est généralement noté O_Q[√5], il est fréquent de ne pas donner de nom à ses éléments.
↑ On les trouve par exemple dans une œuvre de Âryabhata intitulée Âryabhatîya, Georges Ifrah, Histoire universelle des chiffres : L'intelligence des hommes racontée par les nombres et le calcul, Robert Laffont, 1994 (ISBN 978-2-70284212-6)
↑ (en) John Stillwell (en), Mathematics and its History, Springer, 3^e éd., 2010 (ISBN 978-1-44196052-8), p. 72-74
↑ (en) Harold Edwards, Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory, Springer, 3^ème éd., 2000 (ISBN 978-0-387-95002-0)
↑ (en) John J. O’Connor et Edmund F. Robertson, « Fermat's last theorem », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne] .
↑ Dirichlet, Démonstration du théorème de Fermat et de Wilson (compte-rendu par Cournot de quelques mémoires d'Abel, Jacobi et Lejeune-Dirichlet, au Journal de Crelle, t. 3, cah. 4). 1829, t. 11, p. 153-157
↑ Ces résultats sont publiés dans Bruyset (Lyon) et Desaint (Paris), L. Euler et J. L. Lagrange, Éléments d'algèbre, 1774 . Le livre contient contient les Additions aux Éléments d'Algèbre d'Euler par Lagrange, rééditées dans Joseph-Alfred Serret, Œuvres de Lagrange, vol. VII, Gauthier-Villars, 1877 [lire en ligne], p. 5-180 . Elles contiennent les deux preuves citées.

Liens externes

Les cas n=3, 4 et 5 du théorème de Fermat par Robert Ferréol
(en) Présentation des entiers de Dirichlet par Larry Freeman
Théorie algébrique des nombres par Bas Hedixhoven, université de Rennes 1, 2002

Références

Serge Lang, Algèbre [détail des éditions]
Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
(en) David A. Cox, Primes of the Form x²+ny², Wiley, 1997 (ISBN 978-0-47119079-0)
M. Guinot, Arithmétique pour amateurs, Aléas Lyon :
- Vol. 3, Ce diable d'homme d'Euler, 1994 (ISBN 2908016397)
- Vol. 4, Une époque de transition : Lagrange et Legendre, 1996 (ISBN 2908016710)
- Vol. 5, Gauss "princeps mathematicum", 1997 (ISBN 2843010446)

Portail des mathématiques

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Entier de Dirichlet de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Entier De Dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulai … Wikipédia en Français
Entier de dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulai … Wikipédia en Français
Entier De Gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en … Wikipédia en Français
Entier de gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en … Wikipédia en Français
Entier algébrique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces derniers en théorie… … Wikipédia en Français
Entier de Gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en théorie algébrique des nombres, un entier de … Wikipédia en Français
DIRICHLET (P. G. LEJEUNE-) — Avec son ami et contemporain Jacobi et son cadet de quelques années Kummer, Dirichlet constitue la première génération des mathématiciens allemands après Gauss, dont naturellement ils subissent très fortement l’influence; mais, alors que celui ci … Encyclopédie Universelle
Entier Algébrique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces derniers en théorie… … Wikipédia en Français
Entier algebrique — Entier algébrique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces… … Wikipédia en Français
Entier quadratique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe, racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du terme du plus… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Entier de Dirichlet

Sommaire

Éléments d'histoire

Origines

Disquisitiones Arithmeticae

Le travail de Dirichlet

Structures

Définitions

Structure d'anneau

Corps des fractions

Fonctions remarquables

Application conjuguée

Norme

Groupe des unités

Norme

Puissance du nombre d'or

Suite de Fibonacci

Division euclidienne

Existence

Conséquences

Petit théorème de Fermat

Nombres premiers

Définitions et exemples

Résidu quadratique

Equation de Pell-Fermat

Équation

La valeur absolue de d est égale à un

La valeur absolue de d est égale à un nombre premier p

Cas général

Propriété associée à la démonstration du dernier théorème de Fermat

Voir aussi

Notes

Liens externes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Entier de Dirichlet

Sommaire

Éléments d'histoire

Origines

Disquisitiones Arithmeticae

Le travail de Dirichlet

Structures

Définitions

Structure d'anneau

Corps des fractions

Fonctions remarquables

Application conjuguée

Norme

Groupe des unités

Norme

Puissance du nombre d'or

Suite de Fibonacci

Division euclidienne

Existence

Conséquences

Petit théorème de Fermat

Nombres premiers

Définitions et exemples

Résidu quadratique

Equation de Pell-Fermat

Équation

La valeur absolue de d est égale à un

La valeur absolue de d est égale à un nombre premier p

Cas général

Propriété associée à la démonstration du dernier théorème de Fermat

Voir aussi

Notes

Liens externes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link