Theoreme de Stark-Heegner

Theoreme de Stark-Heegner

Théorème de Stark-Heegner

Le théorème de Stark-Heegner est un théorème de la théorie des nombres qui indique précisément quel corps de nombres quadratique imaginaire admet une décomposition en facteurs premiers unique dans leur anneau d'entiers. Il résout un cas particulier du problème du nombre de classes de Gauss pour la détermination du nombre de corps quadratiques imaginaires qui possèdent un nombre de classe fixé donné.

Soit 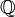\mathbb{Q}\,, l'ensemble des nombres rationnels, et d un entier sans carré (i.e., un produit de nombres premiers distincts) autres que 1. Alors le corps de nombres algébriques 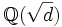\mathbb{Q}(\sqrt{d})\, est une extension finie de 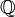\mathbb{Q}\,, appelée une extension quadratique. 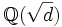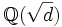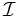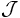Le nombre de classes de \mathbb{Q}(\sqrt{d})\, est le nombre de classes d'équivalence des idéaux de \mathbb{Q}(\sqrt{d})\,, où deux idéaux \mathcal{I}\, et \mathcal{J}\, sont équivalents si et seulement s’il existe des idéaux principaux (a) et (b) tels que 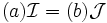(a)\mathcal{I} = (b)\mathcal{J}\,. Ainsi, l'anneau des entiers de 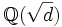\mathbb{Q}(\sqrt{d})\, est un anneau principal, (et par conséquent, un anneau factoriel) si et seulement si le nombre de classes de 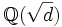\mathbb{Q}(\sqrt{d})\, est égal à 1. Le théorème de Stark-Heegner peut alors être établit comme ce qui suit :

Si d < 0, alors le nombre de classes de 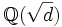\mathbb{Q}(\sqrt{d})\, est égal à 1 si et seulement si d = - 1, - 2, - 3, - 7, - 11, - 19, - 43, - 67, ou - 163.

Ce résultat fut conjecturé en premier par le mathématicien allemand Gauss et démontré par Kurt Heegner en 1952, bien que la démonstration d'Heegner ne fut acceptée jusqu'à ce qu'Harold Stark donne une démonstration en 1967 et il a montré qu'elle était en réalité équivalente à celle d'Heegner.

Si, d'un autre côté, d > 0, alors on ignore s'il existe une infinité de corps 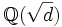\mathbb{Q}(\sqrt{d})\, avec un nombre de classes égal à 1. Les résultats par calculs indiquent qu'il existe un grand nombre de tels corps.

Références

Dorian Goldfeld: Le problème du nombre de classes pour les corps quadratiques imaginaires (en anglais)

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Stark-Heegner ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Stark-Heegner de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Théorème de stark-heegner — Le théorème de Stark Heegner est un théorème de la théorie des nombres qui indique précisément quel corps de nombres quadratique imaginaire admet une décomposition en facteurs premiers unique dans leur anneau d entiers. Il résout un cas… …   Wikipédia en Français

  • Théorème de Stark-Heegner — Le théorème de Stark Heegner est un théorème de la théorie des nombres qui indique précisément quel corps de nombres quadratique imaginaire admet une décomposition en facteurs premiers unique dans leur anneau d entiers. Il résout un cas… …   Wikipédia en Français

  • Nombre De Heegner — En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d entiers possède une factorisation unique. Voir le… …   Wikipédia en Français

  • Nombre d'Heegner — Nombre de Heegner En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d entiers possède une factorisation… …   Wikipédia en Français

  • Nombre de heegner — En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d entiers possède une factorisation unique. Voir le… …   Wikipédia en Français

  • Nombre de Heegner — En théorie des nombres, un nombre de Heegner est un nombre entier positif n tel que le corps quadratique possède un nombre de classes de diviseurs égal à 1. De manière équivalente, son anneau d entiers possède une factorisation unique. Voir le… …   Wikipédia en Français

  • Groupe des classes d'idéaux — En mathématiques, et plus précisément en algèbre, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chacun de ces corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe… …   Wikipédia en Français

  • Groupe Des Classes D'idéaux — En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des classes d idéaux 2 Développement… …   Wikipédia en Français

  • Groupe des classes — d idéaux En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des classes d idéaux 2… …   Wikipédia en Français

  • Groupe des classes d'ideaux — Groupe des classes d idéaux En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”