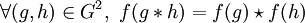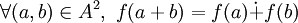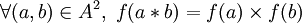- Homomorphisme
-
Morphisme
En mathématiques, un morphisme ou homomorphisme est une application entre deux ensembles munis d'une même espèce de structure algébrique, qui respecte cette structure.
Note : à ne pas confondre avec homéomorphisme
Cette notion est un des concepts de base de la théorie des catégories, où on lui donne une définition formelle bien plus large. Ainsi, un morphisme n'est pas forcément une fonction, c'est juste une flèche reliant deux objets qui ne sont pas forcément des ensembles.
Les morphismes ont des applications particulièrement importantes en physique moderne, en particulier la mécanique quantique.
Sommaire
Définitions
Définition générique
Soient
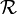 et
et 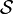 deux relations binaires sur E et F respectivement et
deux relations binaires sur E et F respectivement et 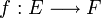 une application de E dans F.
une application de E dans F.f est un morphisme de
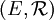 dans
dans 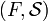 si et seulement si:
si et seulement si: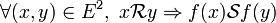
Cas des groupes
Si on est dans le cas de deux groupes
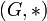 et
et 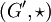 , cette définition se précise de la façon suivante : un morphisme
, cette définition se précise de la façon suivante : un morphisme 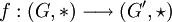 , vérifie :
, vérifie :Cas des anneaux
Dans le cas de deux anneaux
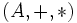 et
et 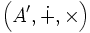 , un morphisme f vérifie donc:
, un morphisme f vérifie donc:si les anneaux considérés sont de plus unitaires, on parle de morphisme unitaire lorsque
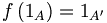 .
.
Un morphisme d'anneaux entre anneaux unitaires n'est pas forcément unitaire, comme le montre l'exemple suivant : si on choisit un ensemble E infini, et une sous-partie F de E finie et que l'on munit les ensembles des parties de ces ensembles de la structure d'anneau où la somme est l'union disjointe et le produit est l'intersection, l'inclusion des parties de F dans les parties de E est un morphisme d'anneau, mais n'est pas un morphisme d'anneau unitaire. En effet, c'est l'ensemble E tout entier qui est élément neutre pour l'intersection dans l'ensemble des parties de E, mais l'élément neutre des parties de F est F. Donc son image par l'inclusion n'est pas l'élément neutre de l'anneau d'arrivée.
De
 dans
dans 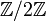 , l'application reste modulo 2 est un morphisme unitaire d'anneaux. L'autre sens n'est pas vrai : il n'existe aucun morphisme d'anneau de
, l'application reste modulo 2 est un morphisme unitaire d'anneaux. L'autre sens n'est pas vrai : il n'existe aucun morphisme d'anneau de 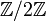 vers
vers  .
.Cas des espaces vectoriels
Dans le cas de deux
 -espaces vectoriels (E, + ,.) et
-espaces vectoriels (E, + ,.) et 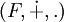 , un morphisme vérifie :
, un morphisme vérifie :- f est un morphisme de groupe pour (E, + ) et
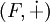
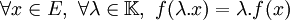
Ce qui est équivalent à :
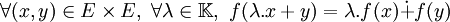
On parle alors d'application linéaire.
Cas des algèbres
Dans le cas de deux
 -algèbres
-algèbres 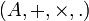 et
et 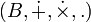 , un morphisme vérifie :
, un morphisme vérifie : est une application linéaire de
est une application linéaire de 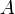 dans
dans 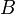 ,
, est un morphisme d’anneaux ;
est un morphisme d’anneaux ;
ce qui est équivalent à :
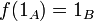 ,
,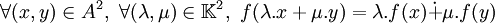 ,
,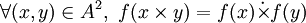 .
.
Cas des ensembles ordonnés
Un morphisme entre deux ensembles ordonnés est une application croissante (une application qui préserve l'ordre) :
Si ( A, ⊑ ) et ( B, ≼ ) sont des ensembles ordonnés et f est une application de A dans B, f est un morphisme si pour tout x et y dans A tels que x ⊑ y, on a f(x) ≼ f(y).
En théorie des ordres, on dit souvent fonction monotone au lieu de fonction croissante ou décroissante.
Classement
- un endomorphisme est un morphisme d'une structure dans elle-même ;
- un isomorphisme est un morphisme f entre deux ensembles munis de la même espèce de structure, tel qu'il existe un morphisme f' dans le sens inverse, tels que
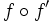 et
et 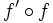 sont les identités des structures ;
sont les identités des structures ; - un automorphisme est un isomorphisme d'une structure dans elle-même, c'est un endomorphisme bijectif ;
- un épimorphisme (ou morphisme épique) est un morphisme
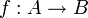 tel que : pour tout couple g,h de morphismes de type
tel que : pour tout couple g,h de morphismes de type 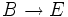 (et donc aussi pour tout E), si
(et donc aussi pour tout E), si 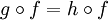 , alors g = h ;
, alors g = h ; - un monomorphisme (ou morphisme monique) est un morphisme
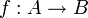 tel que : pour tout couple g,h de morphismes de type
tel que : pour tout couple g,h de morphismes de type 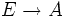 (et donc aussi pour tout E), si
(et donc aussi pour tout E), si 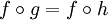 , alors g = h.
, alors g = h.
Exemple : l'identité d'un ensemble est toujours un morphisme, quelle que soit la structure considérée. Et c'est un automorphisme…
Ensembles isomorphes
On dit que les ensembles E et F sont isomorphes s'il existe un isomorphisme de E sur F.
Savoir que deux ensembles sont isomorphes présente un grand intérêt car cela permet de transposer des résultats et propriétés démontrées de l'un à l'autre.
Exemple : le groupe de Klein est isomorphe à
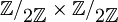 .
.Voir aussi
- Homéomorphisme : isomorphisme d'espace topologique, i.e. application continue et d'inverse continue
- Difféomorphisme : isomorphisme de variété différentielle , c'est-à-dire application à différentielle continue et d'inverse à différentielle continue
- Cryptomorphisme
- Morphisme de graphes
- Portail des mathématiques
Catégories : Algèbre générale | Théorie des catégories
Wikimedia Foundation. 2010.