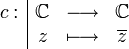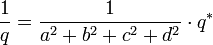Complexe conjugué
- Complexe conjugué
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Complexe conjugué de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
conjugué — conjugué, ée [ kɔ̃ʒyge ] adj. et n. • 1690; « marié » 1596; de conjuguer 1 ♦ Joint, combiné avec. Influences conjuguées. La force conjuguée à, avec l intelligence. L action conjuguée du vent et de la pluie. Grâce à leurs efforts conjugués. 2 ♦… … Encyclopédie Universelle
complexe — [ kɔ̃plɛks ] adj. et n. m. • XIVe ; lat. complexus, de complecti « contenir » I ♦ Adj. 1 ♦ Qui contient, qui réunit plusieurs éléments différents. Question, problème complexe. « Hamlet est un personnage parfaitement humain, parce que complexe »… … Encyclopédie Universelle
complexé — complexe [ kɔ̃plɛks ] adj. et n. m. • XIVe ; lat. complexus, de complecti « contenir » I ♦ Adj. 1 ♦ Qui contient, qui réunit plusieurs éléments différents. Question, problème complexe. « Hamlet est un personnage parfaitement humain, parce que… … Encyclopédie Universelle
Conjugué d'un nombre complexe — Conjugué En mathématiques, le conjugué d un nombre complexe z est le nombre complexe formé de la même partie réelle que z mais de partie imaginaire opposée. Sommaire 1 Définition 2 Propriétés 3 Q … Wikipédia en Français
Conjugue — Conjugué En mathématiques, le conjugué d un nombre complexe z est le nombre complexe formé de la même partie réelle que z mais de partie imaginaire opposée. Sommaire 1 Définition 2 Propriétés 3 Q … Wikipédia en Français
Complexe fendu — Nombre complexe fendu En mathématiques, les nombres complexes fendus sont une extension des nombres réels définis de manière analogue aux nombres complexes (usuels). La différence clef entre les deux est que la multiplication des nombres… … Wikipédia en Français
Conjugué — Pour les articles homonymes, voir Conjugaison (homonymie). En mathématiques, le conjugué d un nombre complexe z est le nombre complexe formé de la même partie réelle que z mais de partie imaginaire opposée. Sommaire 1 … Wikipédia en Français
Plongement complexe — Signature (arithmétique) En théorie algébrique des nombres, la signature d un corps de nombres algébriques est un invariant de ce corps. Elle est définie comme un couple de deux entiers r1 et r2, tels que r1 est le nombre de plongements réels, et … Wikipédia en Français
Nombre Complexe Fendu — En mathématiques, les nombres complexes fendus sont une extension des nombres réels définis de manière analogue aux nombres complexes (usuels). La différence clef entre les deux est que la multiplication des nombres complexes (usuels) respecte la … Wikipédia en Français
Nombre complexe fendu — En mathématiques, les nombres complexes fendus sont une extension des nombres réels définis de manière analogue aux nombres complexes (usuels). La différence clef entre les deux est que la multiplication des nombres complexes (usuels) respecte la … Wikipédia en Français
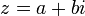 , où a et b sont réels, est
, où a et b sont réels, est 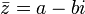 (lu « z barre ») mais est très souvent noté aussi z * ,
(lu « z barre ») mais est très souvent noté aussi z * ,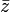 est le symétrique du point d'affixe
est le symétrique du point d'affixe 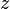 par rapport à l'axe des abscisses.
par rapport à l'axe des abscisses.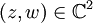 .
.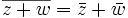
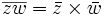
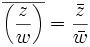 si
si 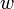 est non nul
est non nul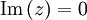 alors
alors 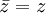
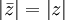
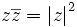
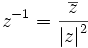 pour z non-nul.
pour z non-nul.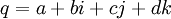 est
est 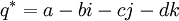 .
.