- Nombre Premier De Gauss
-
Nombre premier de Gauss
En mathématiques et plus précisément en algèbre, un nombre premier de Gauss est une notion de théorie algébrique des nombres concernant les entiers de Gauss.
Un nombre premier de Gauss correspond au concept de nombre premier dans l'anneau des entiers de Gauss.
Les nombres premiers de Gauss sont utilisés pour la résolution d'équations diophantiennes comme le théorème des deux carrés de Fermat ou pour établir des résultats théoriques comme la loi de réciprocité quadratique.
Sommaire
Motivation
En 1801 dans son livre Recherches arithmétiques Carl Friedrich Gauss développe des arithmétiques sur d'autres anneaux que celui des entiers relatifs. Il utilise particulièrement l'anneau des polynômes à coefficients dans un corps et l'ensemble des entiers qui portent son nom. Un entier de Gauss est un nombre complexe dont les parties réelle et imaginaire sont entières.
L'ensemble des entiers de Gauss est un anneau euclidien donc factoriel. Une arithmétique modulaire se développe, analogue à celle de l'anneau Z/nZ. Une connaissance fine de la structure nécessite la compréhension des nombres premiers de Gauss. Elle rend opérationnelle le théorème de composition en facteurs premiers.
Définition et exemples
-
- Un entier de Gauss est dit nombre premier de Gauss ou irréductible si, et seulement si, les seuls diviseurs de cet entier sont les unités ou le produit du nombre par une unité.
La première approche est un peu déconcertante. Certains nombres premiers dans Z ne sont pas des nombres premiers de Gauss :
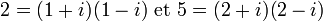
En revanche, 2 + i ou 3 sont irréductibles. Il est relativement simple de caractériser les nombres premiers de Gauss. C'est le rôle du prochain paragraphe.
Propriétés
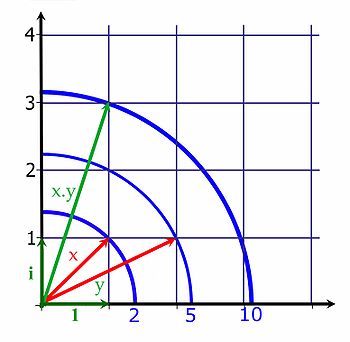
Une notion utile pour l'analyse des entiers de Gauss est la norme arithmétique. Elle est définie comme la somme des carrés de sa partie réelle et imaginaire. Elle est à valeur dans l'ensemble des entiers positifs et est multiplicative : deux entiers x et y vérifie l'égalité N(x.y) = N(x).N(y). La figure de droite illustre cette propriété. La norme est indiqué par le cercle bleu, dans l'exemple la norme de x est égal à deux, celle de y à cinq et le produit possède une norme de dix.
Quelques propositions permettent de caractériser les entiers irréductibles :
-
- Si la norme d'un entier de Gauss est égale à un nombre premier, alors il est un nombre premier de Gauss.
En effet, si u et v sont deux diviseurs d'un entier de Gauss a, alors N(a) = N(u).N(v). En conséquence comme la norme de a est un nombre premier, soit u soit v possède une norme égale à un.
La réciproque n'est pas vraie, par exemple 3 est un entier de Gauss sans diviseur autre que lui-même et 1 au groupe des unités près, cependant sa norme est égale à 9.
Il existe une condition nécessaire et suffisante simple pour caractériser les nombres premiers de Gauss :
-
- Un entier naturel est premier (ou irréductible) au sens des entiers de Gauss si et seulement s'il n'est pas somme de deux carrés.
Elle permet de caractériser précisément les nombres irréductibles :
-
- Un entier de Gauss est irréductible si et seulement si l'une des deux configurations suivantes se produit :
-
- sa norme est un nombre premier et ce nombre premier est congru à 1 modulo 4;
- sa norme est le carré d'un nombre premier congru à 3 modulo 4 et dans ce cas ou sa partie réelle ou sa partie imaginaire est nulle.
Démonstrations-
- Un entier naturel est premier (ou irréductible) au sens des entiers de Gauss si et seulement s'il n'est pas somme de deux carrés.
Soit p un nombre premier, supposons qu'il est somme de deux carrés:
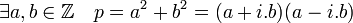
Alors p admet deux diviseurs non unitaires car de norme égale à p.
Supposons qu'il ne soit pas irréductible, alors il existe deux entiers de Gauss α et β non unitaires tel que p = α.β et comme la norme de p est égale à p2 la norme de α est égale à p. La norme est somme de deux carrés, ce qui termine la démonstration.
-
- Un nombre premier p impaire est somme de deux carrés si et seulement s'il est congru à 1 modulo 4.
La démonstration est donnée dans l'article sur la démonstration du théorème des deux carrés de Fermat par Dedekind
-
- Un entier n est somme de deux carrés d'entiers si et seulement si dans sa décomposition en facteurs premiers, les nombres premiers congrus à trois modulo 4 figurent à une puissance paire.
La démonstration est donnée dans l'article sur la généralisation à tous les entiers du théorème des deux carrés de Fermat
-
- Condition nécessaire et suffisante pour qu'un entier n soit irréductible :
Cas où N(x) est premier :
Alors x est premier et pour qu'un nombre premier supérieur à 3 soit une norme, il faut et il suffit qu'il soit congru à 1 modulo 4.
Cas où N(x) est le carré d'un nombre premier p congru à 3 modulo 4 :
Soit u et v une décomposition en deux facteurs de x. Alors si la norme de u est différente de 1, comme elle ne peut être égale à p car une telle valeur n'est pas une norme, elle est égale à la norme de x. On en déduit que x est irréductible.
De plus, N(x) n'est somme de deux carrés que si chacun des membres est un multiple de p2. Ceci démontre que soit la partie réelle, soit la partie imaginaire est nulle.
Cas où il existe un facteur premier congru à 3 modulo 4 à une puissance impair :
Un tel facteur n'est pas somme de deux carrés, il n'existe donc pas d'entier de Gauss ayant cette valeur pour norme.
Cas où N(x) est une somme de deux carrés, non première et non carré d'un nombre premier p congru à 3 modulo 4.
Montrons avec un raisonnement par l'absurde que x n'est pas irréductible. Supposons qu'il le soit et trouvons une contradiction. N(x) est le produit de deux sommes de deux carrés chacune différente de 1 (c'est une conséquence de la démonstration du cas général du théorème des deux carrés. Il existe donc u et v tel que N(x) = N(u.v). On en déduit :
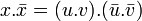
Si x est irréductible alors x divise l'un des facteurs de droite, par exemple u.v. et il existe un entier α tel que α.x = u.v. Comme la norme de x est égale à celle de u.v, la norme de α est égale à 1 et α est une unité. On en déduit que x = α-1u.v. Ce qui prouve que x n'est pas irréductible d'où une contradiction et la démonstration est achevée.
Voir aussi
Liens externes
- (fr) Entier de Gauss Vincent Lefèvre
- (en) Applet de factorisation des entiers de Gauss
- (fr) Théorie algébrique des nombres Bas Hedixhoven Université de Rennes 1 2002
Références
- S. Lang Algebre Dunod 2004
- P. Samuel Théorie algébrique des nombres Hermann Paris 1971
- J-P Serre Cours d'arithmétique Presses Universitaires de France Paris 1977
- Portail des mathématiques
Catégories : Entier quadratique | Théorie des anneaux | Carl Friedrich Gauss | Arithmétique modulaire -
Wikimedia Foundation. 2010.