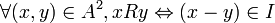- Anneau Quotient
-
Anneau quotient
En mathématiques, un anneau quotient est l'ensemble quotient d'un anneau donné par un de ses idéaux.
Sommaire
Définition
Soient A un anneau et I un idéal bilatère de A. On définit la relation d'équivalence R suivante :
Deux éléments de A sont ainsi en relation si leur différence appartient à l'idéal I, c’est-à-dire si x et y sont congrus modulo I.
L'ensemble quotient A / R, que l'on note alors A / I, muni des opérations induites par I
- (x + I) + (y + I) = x + y + I et
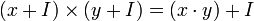
est un anneau, nommé anneau quotient de A par I.
Exemples
- Si I = A, A / A est l'anneau trivial {0}.
- Si I = {0}, A / {0} est isomorphe à A.
- Si
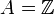 et
et 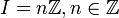 , on note l'anneau quotient Z/nZ. Cette structure est le fondement de l'arithmétique modulaire.
, on note l'anneau quotient Z/nZ. Cette structure est le fondement de l'arithmétique modulaire.
Propriétés
L'application
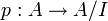 définie par p(x) = x + I est un homomorphisme surjectif d'anneau dont le noyau est l'idéal I.
définie par p(x) = x + I est un homomorphisme surjectif d'anneau dont le noyau est l'idéal I.Soit A un anneau commutatif :
- I est premier si et seulement si A / I est un anneau intègre.
- I est maximal si et seulement si A / I est un corps
Démonstration- I premier ssi A / I est intègre.
- Preuves directes :
Si I est premier, montrons que A / I est intègre : considérons un produit nul xy = 0 dans A / I. Cela signifie que
 . Or I est premier, donc x ou y appartient à I, donc x = 0 ou y = 0 dans A / I. Conclusion : I est intègre.
. Or I est premier, donc x ou y appartient à I, donc x = 0 ou y = 0 dans A / I. Conclusion : I est intègre.Réciproquement, si A / I est intègre, montrons que I est premier : considérons un produit
 . Alors xy = 0 dans A / I. Comme A / I est intègre, x=0 ou y=0 dans A / I, donc
. Alors xy = 0 dans A / I. Comme A / I est intègre, x=0 ou y=0 dans A / I, donc  ou
ou 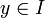 . Conclusion : I est premier.
. Conclusion : I est premier.- Preuves par l'absurde :
Si A / I n'est pas intègre alors il existe a et b, non nuls, dans A / I tels que ab = 0. Soit a' et b' deux éléments de leurs images réciproques, alors a' n'est pas dans I sinon son image serait nul, il en est de même pour b', par contre leur produit est dans I vu que l'image de ce produit est nul, ainsi l'on a deux éléments qui ne sont pas dans I et dont le produit l'est. I ne peut-être premier.
A l'inverse supposons que I n'est pas premier, ils existent alors a' et b' qui ne sont pas dans I mais dont le produit l'est. Les images de a' et de b' par la projection ne sont pas nulles alors que l'image du produit l'est. On a donc que A / I n'est pas intègre.
- I maximal ssi A / I est un corps.
- Preuves directes :
Si I est maximal alors pour tout
 on a
on a  , autrement dit il existe
, autrement dit il existe 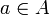 tel que
tel que  , donc x inversible. Ainsi tout élément non nul de A / I est inversible.
, donc x inversible. Ainsi tout élément non nul de A / I est inversible.Réciproquement, si A / I est un corps alors pour tout
 , alors x est non nul dans A / I, donc inversible, donc il existe
, alors x est non nul dans A / I, donc inversible, donc il existe 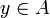 tel que
tel que  , ou encore
, ou encore 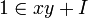 . Ceci étant vrai pour tout
. Ceci étant vrai pour tout  , on obtient I maximal.
, on obtient I maximal.- Preuves par l'absurde :
Supposons que I n'est pas maximal et soit J un idéal strictement compris entre I et A. On aurait alors un morphisme non injectif (surjectif, mais cela n'est pas important) de A / I sur A / J. Or un morphisme d'anneau partant d'un corps est injectif et donc A / I n'est pas un corps.
A l'inverse supposons que A / I n'est pas un corps. Il possède donc un idéal non trivial, dont l'image réciproque serait un idéal de A strictement compris entre A et I. Et I ne serait alors pas un idéal maximal.
Si f est un morphisme d'anneaux de A vers B, notons
 son noyau. Alors f se factorise en un morphisme injectif
son noyau. Alors f se factorise en un morphisme injectif 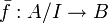 défini par
défini par 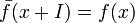 .
.Utilisations
Théorie algébrique des nombres
Les anneaux quotients sont utilisés dans de nombreuses branches des mathématiques. Les exemples sont fréquents en théorie algébrique des nombres, par exemple pour résoudre des équations diophantiennes. C'est-à-dire des équations à coefficients dans l'ensemble Z des nombres entiers dont les solutions recherchées sont entières.
L'identité de Bézout peut être vu comme une équation diophantienne de degré un, c'est-à-dire qu'elle correspond à un polynôme de degré un. Elle peut prendre la forme suivante :
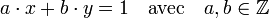
Une solution peut être vu comme l'inverse de a dans l'anneau quotient Z/bZ. Ainsi, il existe des solutions si et seulement si a est élément du groupe des unités de l'anneau quotient, c'est-à-dire le groupe des éléments inversibles de l'anneau. Or a est inversible si et seulement si il est premier avec b. Les valeurs possibles de x sont éléments de l'inverse de la classe de a.
Les équations diophantiennes polynomiales d'ordre deux utilisent aussi la structure d'anneau quotient. Un exemple est un cas particulier de l'équation de Pell-Fermat :

Ici, n désigne un entier sans facteur carré. La méthode chakravala correspond à un algorithme simple de détermination d'une solution. Pour montrer sa convergence, on utilise l'anneau des nombres de la forme a + b.√n où a et b désigne des entiers. Le fait de montrer que tous les anneaux quotients sont de cardinal fini est une étape clé de la démonstration.
Cette équation est analogue à la suivante :
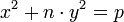
Ici n est toujours un entier sans facteur carré et p désigne un nombre premier. L'usage d'un bon anneau A d'entiers quadratiques, c'est-à-dire de nombres de la forme a + b.i.√n où i désigne l'imaginaire pur et l'étude des anneaux quotients de la forme A/J où J est un idéal maximal permet de résoudre l'équation. Des exemples sont donnés dans l'article Entier quadratique.
Théorie de Galois
La théorie de Galois fait aussi un large usage des anneaux quotients. Soit K un corps commutatif et K[X] l'anneau des polynômes à coefficients dans K. Un des nombreux objectifs de la théorie est l'étude de l'équation polynomiale P(X) = 0. Si P est un polynôme irréductible, on recherche des solutions dans une extension algébrique L de K. Un cas particulier largement utilisé est l'anneau K[X]/(P) des polynômes quotientés par l'idéal engendré par P(X). Comme P(X) est irréductible, l'idéal engendré par P(X) est maximal, l'anneau quotient est bien un corps.
Cette technique permet de construire tous les corps finis. Soit L un corps fini, il existe toujours p un nombre premier et n un entier positif tel que le cardinal de L soit égal à pn. La valeur p correspond à la caractéristique de K. Si P(X) est un polynôme irréductible à coefficients dans l'anneau Z/pZ qui est aussi un corps noté Fp, alors le corps L est isomorphe au quotient de l'anneau Fp[X] par l'idéal engendré par P(X).
- Portail des mathématiques
Catégorie : Idéal
Wikimedia Foundation. 2010.