Homeomorphisme

Homeomorphisme

Homéomorphisme

Une tasse est homéomorphe à un tore.

En topologie, un homéomorphisme est une application bijective continue entre deux espaces topologiques dont la réciproque est continue. Dans ce cas, les deux espaces topologiques sont dits homéomorphes.

La notion d'homéomorphisme est la bonne notion pour dire que deux espaces topologiques sont « le même » vu différemment. C'est la raison pour laquelle les homéomorphismes sont les isomorphismes de la catégorie des espaces topologiques.

En général, une application continue bijective n'a aucune raison d'avoir un inverse continu. Par exemple, l'application 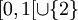[0,1[\cup \{2\} sur [0,1] égale à l'identité sur [0,1[ et envoyant 2 sur 1 est une bijection continue mais sa réciproque n'est pas continue en 1.

  • Une bijection continue ouverte ou fermée est un homéomorphisme.
  • Soit K un espace topologique compact, E un espace topologique séparé, et 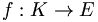f:K\rightarrow E une bijection continue. Alors f est un homéomorphisme. En particulier, E est un compact.

En effet, toute partie fermée de K est un compact ; comme E est séparé, l'image par f d'une partie fermée de K est un compact, a fortiori une partie fermée de E. Donc, f est une application continue bijective fermée, ie un homéomorphisme par le point précédent.

Vous pouvez visualiser l'action d'un homéomorphisme du plan sur un carré avec une petite animation sur geogebra puis, il est intéressant de définir explicitement cet homéomorphisme en suivant l'activité proposée.

Articles connexes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Hom%C3%A9omorphisme ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Homeomorphisme de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • homéomorphisme — [ ɔmeɔmɔrfism ] n. m. • 1926; de homéomorphe ♦ Math., log. Bijection qui, à deux éléments voisins d un ensemble, fait correspondre deux éléments également voisins d un autre. ● homéomorphisme nom masculin Phénomène relatif aux analogies des… …   Encyclopédie Universelle

  • Homéomorphisme — Une tasse est homéomorphe à un tore. En topologie, un homéomorphisme est une application bijective continue entre deux espaces topologiques dont la réciproque est continue. Dans ce cas, les deux espaces topologiques sont dits homéomorphes. La… …   Wikipédia en Français

  • homéomorphisme — (o mé o mor fi sm ) s. m. État de ce qui est homéomorphe. SUPPLÉMENT AU DICTIONNAIRE    HOMÉOMORPHISME. Ajoutez :    Synonyme de plésiomorphisme …   Dictionnaire de la Langue Française d'Émile Littré

  • Homéomorphe — Homéomorphisme Une tasse est homéomorphe à un tore. En topologie, un homéomorphisme est une application bijective continue entre deux espaces topologiques dont la réciproque est continue. Dans ce cas, les deux espaces topologiques sont dits… …   Wikipédia en Français

  • SYSTÈMES DYNAMIQUES DIFFÉRENTIABLES — Sans doute née avec le mémoire que Poincaré écrivit en 1881 «sur les courbes définies par des équations différentielles», où l’étude quantitative (analytique) locale des équations différentielles dans le champ complexe est remplacée par leur… …   Encyclopédie Universelle

  • Revêtement (mathématiques) — Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints Si sont projeté …   Wikipédia en Français

  • Espace vectoriel normé de dimension finie — Topologie d un espace vectoriel de dimension finie En mathématiques, la topologie d un espace vectoriel de dimension finie correspond à un cas particulier d espace vectoriel normé. Cette configuration se produit si la dimension est finie. Elle… …   Wikipédia en Français

  • Revetement (mathematiques) — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revêtement (mathématique) — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revêtement galoisien — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”