Diffeomorphisme
- Diffeomorphisme
-
Difféomorphisme
On dit que f est un difféomorphisme de O dans F si
- f est injective sur O ( bijective de O dans f(O) )
- f est différentiable sur O, sa réciproque est différentiable sur f(O)
Un 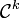 -difféomorphisme est une fonction
-difféomorphisme est une fonction 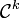 , bijective, et dont la réciproque est également
, bijective, et dont la réciproque est également 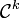 . Montrer qu'une application est un difféomorphisme n'est pas toujours aisé. Le théorème d'inversion locale apporte certains éléments, mais dans le cas général, ils sont insuffisants pour conclure.
. Montrer qu'une application est un difféomorphisme n'est pas toujours aisé. Le théorème d'inversion locale apporte certains éléments, mais dans le cas général, ils sont insuffisants pour conclure.
Cas des fonctions de variable réelle : Une fonction f d'un intervalle I sur un intervalle J est un Ck-difféomorphisme si et seulement si f est de classe Ck sur I et la dérivée de f ne s'annule pas sur I.
Articles connexes
Zoologie
 Portail des mathématiques
Portail des mathématiques
Catégorie : Analyse à plusieurs variables
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Diffeomorphisme de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
difféomorphisme — ● difféomorphisme nom masculin Difféomorphisme de classe C1, bijection f entre deux ouverts U et V, respectivement inclus dans E et F, espaces vectoriels normés sur R (ou C), qui est continûment différentiable ainsi que son application réciproque … Encyclopédie Universelle
Difféomorphisme — En mathématiques, un difféomorphisme est un isomorphisme dans la catégorie des variétés différentielles : c est une bijection différentiable d une variété dans une autre, dont la bijection réciproque est aussi différentiable. Image d une… … Wikipédia en Français
Diffeomorphisme hamiltonien — Difféomorphisme hamiltonien En mathématiques, les difféomorphismes hamiltoniens sont les difféomorphismes des variétés symplectiques obtenus dans les flots hamiltoniens. Sommaire 1 Définition et exemples 2 Groupe des difféomorphismes hamiltoniens … Wikipédia en Français
Difféomorphisme Hamiltonien — En mathématiques, les difféomorphismes hamiltoniens sont les difféomorphismes des variétés symplectiques obtenus dans les flots hamiltoniens. Sommaire 1 Définition et exemples 2 Groupe des difféomorphismes hamiltoniens 3 Références … Wikipédia en Français
Difféomorphisme de classe C1 — ● Difféomorphisme de classe C1 bijection f entre deux ouverts U et V, respectivement inclus dans E et F, espaces vectoriels normés sur R (ou C), qui est continûment différentiable ainsi que son application réciproque f−1 … Encyclopédie Universelle
Difféomorphisme hamiltonien — En mathématiques, les difféomorphismes hamiltoniens sont les difféomorphismes des variétés symplectiques obtenus dans les flots hamiltoniens. Sommaire 1 Définition et exemples 2 Groupe des difféomorphismes hamiltoniens 3 Références … Wikipédia en Français
SYSTÈMES DYNAMIQUES DIFFÉRENTIABLES — Sans doute née avec le mémoire que Poincaré écrivit en 1881 «sur les courbes définies par des équations différentielles», où l’étude quantitative (analytique) locale des équations différentielles dans le champ complexe est remplacée par leur… … Encyclopédie Universelle
SINGULARITÉS DES FONCTIONS DIFFÉRENTIABLES (la théorie mathématique et ses applications) — De la topologie différentielle à la dynamique qualitative, en passant par la géométrie analytique et la topologie algébrique, les «singularités» ont bien des incarnations en mathématiques; mais cela n’exclut pas une certaine unité: qu’il s’agisse … Encyclopédie Universelle
Lexique De La Géométrie Symplectique — Cette page est une annexe de : Géométrie symplectique Lexique de la géométrie symplectique Annexe de : Géométrie symplectique Cette page rassemble un ensemble de termes pouvant être rencontrés en géom … Wikipédia en Français
Lexique de la géométrie symplectique — Cette page rassemble un ensemble de termes pouvant être rencontrés en géométrie symplectique. Action Pour un Hamiltonien H défini sur une variété symplectique (M,ω) dont le second groupe fondamental est annulé par la forme symplectique, l action… … Wikipédia en Français
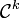 -difféomorphisme est une fonction
-difféomorphisme est une fonction 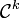 , bijective, et dont la réciproque est également
, bijective, et dont la réciproque est également 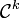 . Montrer qu'une application est un difféomorphisme n'est pas toujours aisé. Le théorème d'inversion locale apporte certains éléments, mais dans le cas général, ils sont insuffisants pour conclure.
. Montrer qu'une application est un difféomorphisme n'est pas toujours aisé. Le théorème d'inversion locale apporte certains éléments, mais dans le cas général, ils sont insuffisants pour conclure.