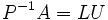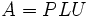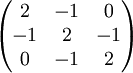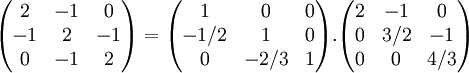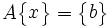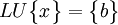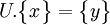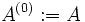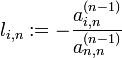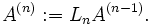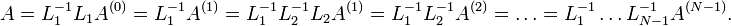Décomposition lu

Décomposition LU

En algèbre linéaire, la décomposition LU est une méthode de décomposition d'une matrice en une matrice triangulaire inférieure L (comme "Low", bas) et une matrice triangulaire supérieure U (comme "Up", haut). Cette décomposition est utilisée en analyse numérique pour résoudre des systèmes d'équations linéaires.

Définition

Soit A une matrice inversible. La matrice A peut être décomposée ainsi

$P^{-1}A = L U \;$

$A = P L U \;$

où P est une matrice de permutation (de même pour P^-1), L est une matrice triangulaire inférieure avec des 1 sur la diagonale et U une matrice triangulaire supérieure. Parfois, la matrice de passage P peut être choisie afin d'être une matrice identité. Dans ce cas, la décomposition devient $A = L U .$

Exemple

Soit par exemple la matrice :

$\begin{pmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \\ \end{pmatrix}$

Cette matrice se factorise en un produit d'une matrice triangulaire inférieure par une matrice triangulaire supérieure de la façon suivante :

$\begin{pmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \\ \end{pmatrix} =\begin{pmatrix} 1 & 0 & 0 \\ -1/2 & 1 & 0 \\ 0 & -2/3 & 1 \\ \end{pmatrix}.\begin{pmatrix} 2 & -1 & 0 \\ 0 & 3/2 & -1 \\ 0 & 0 & 4/3 \\ \end{pmatrix}$

Applications

Résoudre un système d'équations linéaires

Cette factorisation matricielle permet de résoudre des systèmes d'équations linéaires où les coefficients des inconnues sont les mêmes, mais avec plusieurs seconds membres différents. Soit à déterminer le vecteur d'inconnues {x} associé au second membre {b} :

$A \begin{Bmatrix}x\end{Bmatrix}= \begin{Bmatrix}b\end{Bmatrix}$

Ce problème est donc équivalent à la résolution de

$L U \begin{Bmatrix}x\end{Bmatrix}= \begin{Bmatrix}b\end{Bmatrix}$

ou encore

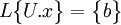$L \begin{Bmatrix} U.x \end{Bmatrix}=\begin{Bmatrix}b\end{Bmatrix}$ que l'on peut mettre, en posant 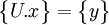$\begin{Bmatrix}U.x\end{Bmatrix}= \begin{Bmatrix}y\end{Bmatrix}$ sous la forme :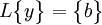 $L \begin{Bmatrix}y\end{Bmatrix}= \begin{Bmatrix}b\end{Bmatrix}$

On trouve les composantes de y par des substitutions élémentaires, puisque d'abord 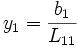$y_1 = \frac{b_1}{L_{11}}$ , puis 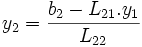$y_2 = \frac{b_2-L_{21}.y_1}{L_{22}}$ , etc.

Cette étape est appelée descente, puisqu'on résout le système en descendant de $y 1$ à $y n$ . Il reste à calculer les composantes du vecteur {x} en résolvant le système triangulaire supérieur :

$U.\begin{Bmatrix}x\end{Bmatrix}= \begin{Bmatrix}y\end{Bmatrix}$

ce qui se fait de manière similaire, mais en calculant d'abord $x n$

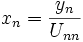$x_n = \frac{y_n}{U_{nn}}$ , etc. en remontant (étape dite de remontée).

Remarque. - Les matrices triangulaires L et U auraient pu être inversées aisément en utilisant l'élimination de Gauss-Jordan. Mais si l'on compte simplement le nombre d'opérations que cela représente pour un système à n équations, on trouvera que la complexité algorithmique du calcul des matrices inverses est supérieure, de sorte que si l'on veut résoudre ce système pour divers b, il est plus intéressant de réaliser la décomposition LU une fois pour toute et d'effectuer les substitutions de descente-remontée pour les différents b plutôt que d'utiliser l'élimination de Gauss-Jordan à de multiples reprises. Ainsi, dans la plupart des publications d'analyse numérique, lorsque la matrice A a été factorisée sous forme LU ou Cholesky (cf. infra, § Le cas symétrique ), on écrit par abus $b = A - 1 x$ pour signifier que le calcul de b peut se faire par cette méthode de descente-remontée. Il est sous-entendu qu'il n'est absolument pas question d'utiliser l'algorithme en calculant la matrice inverse $A - 1$ de A, ce qui serait inutilement coûteux en temps de calcul.

Inverser une matrice

Les matrices L et U peuvent être utilisées pour déterminer l'inverse d'une matrice. Les programmes informatiques qui implémentent ce type de calcul, utilisent généralement cette méthode.

Calcul d'un déterminant

Si A est sous forme LU ou PLU, son déterminant se calcule facilement : $det(A) = det(P)det(L)det(U)$ . Les trois déterminants de ce produit sont très simples à calculer (matrices triangulaires ou de permutations).

Existence, unicité

Pour toute matrice carrée, on a existence d'une décomposition PLU. La décomposition LU existe si et seulement si toutes les sous matrices principales d'ordre 1 à n-1 sont inversibles. Si toutes les sous matrices principales d'ordre 1 à n sont inversibles, elle est unique^[1].

Calcul de la décomposition

Idée principale

La décomposition LU est une forme particulière d'élimination de Gauss Jordan. On transforme la matrice A en une matrice triangulaire supérieure U en éliminant les éléments sous la diagonale. Les éliminations se font colonne après colonne, en commencant par la gauche, en multipliant A par la gauche avec une matrice triangulaire inférieure.

Algorithme

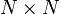
Étant donné une matrice de dimension $N \times N$

$A= (a_{n,n})\;$

on définit

$A^{(0)} := A\;$

et les itérations se font pour n = 1,...,N-1 de la manière suivante.

Sur nième colonne de A^(n-1), on élimine les éléments sous la diagonale en ajoutant à la ième ligne de cette matrice, la nième ligne multipliée par

$l_{i,n} := -\frac{a_{i,n}^{(n-1)}}{a_{n,n}^{(n-1)}}$

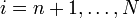pour $i = n+1,\ldots,N$ . Ceci peut être fait en multipliant par la gauche A^(n-1) avec la matrice triangulaire inférieure

$L_n = \begin{pmatrix} 1 & & & & & 0 \\ & \ddots & & & & \\ & & 1 & & & \\ & & l_{n+1,n} & \ddots & & \\ & & \vdots & & \ddots & \\ 0 & & l_{N,n} & & & 1 \\ \end{pmatrix}.$

$A^{(n)} := L_n A^{(n-1)}.\;$

Après N-1 itérations, nous avons éliminé tous les éléments sous la diagonale, par conséquent, nous avons maintenant une matrice triangulaire supérieure A^(N-1).

Nous obtenons la décomposition

$A = L_{1}^{-1} L_{1} A^{(0)} = L_{1}^{-1} A^{(1)} = L_{1}^{-1} L_{2}^{-1} L_{2} A^{(1)} = L_{1}^{-1}L_{2}^{-1} A^{(2)} =\ldots = L_{1}^{-1} \ldots L_{N-1}^{-1} A^{(N-1)}.$

Notons U la matrice triangulaire supérieure A^(N-1) et 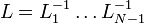$L=L_{1}^{-1} \ldots L_{N-1}^{-1}$ . Sachant que l'inverse d'une matrice triangulaire inférieure est aussi une matrice triangulaire inférieure et que le produit de 2 matrices triangulaires inférieures est encore une matrice triangulaire inférieure, L est donc une matrice triangulaire inférieure. On obtient $A = L U$ .

Au vu de l'algorithme, il est nécessaire que 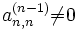$a_{n,n}^{(n-1)}\not=0$ à chaque itération (voir la définition de $l i, n$ ). Si, au cours du calcul, ce cas de figure venait à se produire, il faut intervertir la nième ligne avec une autre pour pouvoir continuer (il est toujours possible de trouver un élément non nul sur la colonne qui pose problème car la matrice est inversible). C'est la raison pour laquelle la décomposition LU s'écrit généralement $P - 1 A = L U$ .

Le cas symétrique

Si la matrice A est une matrice symétrique, il existe une décomposition dite factorisation de Crout

A = L . D . t L

où L est une matrice triangulaire inférieure dont la diagonale ne comprend que des 1, $t L$ est la transposée de L, et D est une matrice diagonale.

Si la matrice A est symétrique définie positive, il existe une décomposition plus simple, donnée par la méthode de Cholesky

A = L . t L

où L est une matrice triangulaire inférieure à diagonale positive et $t L$ est la transposée de L.

Notes et références

↑ Pour la démonstration, cf. Ciarlet, chap. 4, §4.3

P. G. Ciarlet - « Introduction à l'analyse numérique matricielle et à l'optimisation » (1985, rééd. 2001), éd. Masson, coll. Math. Appl. pour la Maîtrise (ISBN 2-225-68893-1)

Voir aussi

Articles en rapport avec les matrices
Par forme	carrée • triangulaire • diagonale • tridiagonale • élémentaire • échelonnée • creuse • aléatoire • circulante • de Hankel • de Toeplitz • de Vandermonde
Transformée	transposée • adjointe • inverse • Comatrice
En relation	équivalente • semblable • congruente
Par propriété	inversible • diagonalisable • trigonalisable • symétrique • antisymétrique • hermitienne • normale • orthogonale • unitaire • symplectique • de Hadamard • définie positive • à diagonale dominante • nilpotente
Par famille	identité • de De Casteljau • de Cartan • de Hilbert • de Mueller • de Pauli • de Dirac
Particulière	CKM
Associée	de permutation • de passage • compagnon • de Sylvester • d'adjacence • laplacienne • hessienne • jacobienne • génératrice • de contrôle • de corrélation • de Gram • de variance-covariance • d'inertie • de Jones • des gains • stochastique
Résultats	décompositions : LU • QR • polaire • valeurs singulières Trigonalisation • Réduction de Jordan • facteurs invariants
Voir aussi	Théorie des matrices • Algèbre linéaire

(fr) Décomposition LU

Portail des mathématiques

Ce document provient de « D%C3%A9composition LU ».

Catégorie : Analyse numérique matricielle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Décomposition lu de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

décomposition — [ dekɔ̃pozisjɔ̃ ] n. f. • 1694; de décomposer, d apr. composition 1 ♦ Séparation (d un corps, d une substance) en ses éléments. ⇒ division, séparation. Décomposition chimique. Décomposition de la lumière par le prisme. Math. Décomposition d une… … Encyclopédie Universelle
Decomposition LU — Décomposition LU En algèbre linéaire, la décomposition LU est une méthode de décomposition d une matrice en une matrice triangulaire inférieure L (comme Low , bas) et une matrice triangulaire supérieure U (comme Up , haut). Cette décomposition… … Wikipédia en Français
Decomposition QR — Décomposition QR En algèbre linéaire, la décomposition QR (appelée aussi, décomposition QU) d une matrice A est une décomposition de la forme A = QR où Q est une matrice orthogonale (QQT = I), et R une matrice triangulaire supérieure. Il existe… … Wikipédia en Français
Decomposition — Décomposition Pour les articles homonymes, voir décomposition (homonymie). En biologie, la décomposition est le processus par lequel de la matière autrefois vivante dégénère pour atteindre une forme plus simple de matière (la matière minérale).… … Wikipédia en Français
décomposition — DÉCOMPOSITION. sub. f. Terme de Chimie. Dissolution, résolution d un corps mixte dans ses principes. La décomposition d un corps mixte. f♛/b] On dit aussi au figuré, La décomposition d une idée, d un discours.[b]Décomposition, en Mécanique. On… … Dictionnaire de l'Académie Française 1798
Decomposition — De*com po*si tion, n. [Pref. de (in sense 3 intensive) + composition: cf. F. d[ e]composition. Cf. {Decomposition}.] 1. The act or process of resolving the constituent parts of a compound body or substance into its elementary parts; separation… … The Collaborative International Dictionary of English
decomposition — decomposition; pho·to·decomposition; … English syllables
decomposition — Decomposition. s. f. v. Terme de Chymie. Dissolution, resolution d un corps mixte dans ses principes. La decomposition d un corps mixte … Dictionnaire de l'Académie française
decomposition — index consumption, destruction, deterioration, dissolution (disintegration), spoilage Burton s Legal Thesaurus. William C. Burton … Law dictionary
decomposition — 1762, from DE (Cf. de ) + COMPOSITION (Cf. composition). An earlier word in the same form meant further compounding of already composite things (1650s) … Etymology dictionary

Dictionnaires et Encyclopédies sur 'Academic'

Décomposition lu