Matrices semi-simples

Matrices semi-simples

Matrice semi-simple

En algèbre linéaire, la notion de matrice semi-simple constitue une généralisation de la notion de matrice diagonalisable. Elle permet de discriminer deux types d'obstruction à la diagonalisabilité : d'une part les obstructions liées à l'arithmétique du corps de coefficients dans lequel la matrice est considérée, et d'autre part les obstructions qui demeurent indépendantes de ce corps.

Une matrice A à coefficients dans un corps \mathbb{K} est dite semi-simple sur \mathbb{K} si tout sous-espace invariant par A possède un supplémentaire invariant par A.

Sommaire

Résultats généraux

La semi-simplicité se caractérise à l'aide du polynôme minimal de la matrice considérée : une matrice à coefficients dans \mathbb{K} est semi-simple si et seulement si son polynôme minimal est sans facteur carré (c'est-à-dire qu'il n'admet aucun diviseur qui soit le carré d'un autre polynôme) dans \mathbb{K}[X].

En particulier, dans le cas où toutes les racines du polynôme minimal de A appartiennent à \mathbb{K}, ceci se particularise en : A est semi-simple si et seulement si elle est diagonalisable.

Si le corps des coefficients a la propriété d'être parfait (par exemple tout corps de caractéristique nulle, comme le corps des nombres rationnels ou le corps des nombres réels, ou tout corps fini), c'est-à-dire que tous les polynômes irréductibles à coefficients dans ce corps n'ont que des racines simples dans une clôture algébrique de ce corps, la caractérisation peut s'écrire : une matrice est semi-simple si et seulement si elle est diagonalisable dans une clôture algébrique du corps.


Démonstration

Si le polynôme minimal M de A admet un carré P2 comme diviseur, alors la matrice A n'est pas semi-simple. En effet, le sous-espace Im(P(A)) est dans ce cas un sous-espace stable, et, si S désigne un supplémentaire stable de ce sous-espace, alors 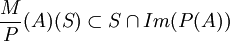\frac{M}{P}(A)(S)\subset S\cap Im(P(A)) d'une part par stabilité, et d'autre part, car P divise M/P. Il s'en suit que M/P est un polynôme annulateur de A, en contradiction avec la définition de polynôme minimal. Réciproquement, si le polynôme minimal M de A est sans facteur carré, que S désigne un sous-espace stable par A, alors le polynôme minimal N de A considéré en restriction à S est un diviseur de M. On vérifie alors que S est le noyau de N(A), et admet comme supplémentaire stable le noyau de M/N(A), d'après le lemme des noyaux.

Dans le cas d'un corps parfait, le polynôme minimal est sans facteur carré si et seulement s'il est séparable, c'est-à-dire qu'il se scinde en facteurs simples dans une clôture algébrique de K. On reconnaît bien une caractérisation classique de la diagonalisabilité dans une clôture algébrique.

Un exemple dans un corps non parfait

Les définitions et résultats qui précèdent peuvent dépendre du corps \mathbb{K} dans lequel on se place.

Voici un exemple quelque peu pathologique, qui permet d'observer certaines subtilités.

Soit 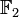\mathbb{F}_2 le corps à deux éléments, et soit 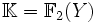\mathbb{K}=\mathbb{F}_2(Y), le corps des fractions rationnelles sur 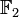\mathbb{F}_2. Définissons la matrice

A=\begin{pmatrix} 0&Y\\1&0 \end{pmatrix}.

Le polynôme caractéristique de cette matrice est χA(Z) = Z2 − Y, dont le terme constant Y n'est pas un carré dans les fractions rationnelles à coefficients dans 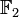\mathbb{F}_2. En effet, si c'était le carré de p(Y) / q(Y), on devrait avoir Yq(Y)2 = p(Y)2. Le premier membre de cette relation est de degré impair en Y et son second membre est de degré pair, il y a donc une contradiction. Le polynôme χA est donc irréductible : s'il admettait une factorisation, celle-ci serait de la forme Z2 − Y = (aY + b)(cY + d). On aurait donc ac = 1, ad + bc = 0 et bd = Y, d'où l'on tire a2d2 = Y et on a une contradiction. Ceci montre que la matrice A n'a pas de valeur propre dans \mathbb{K}. Elle est donc semi-simple sur \mathbb{K}.

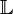On considère maintenant l'extension \mathbb{L}=\mathbb{K}[Y]/(Y-X^2), obtenue en adjoignant à \mathbb{K} une racine carrée de Y, notée X. On vérifie très facilement que \mathbb{L} est bien un corps, qui contient \mathbb{K} ; c'est le corps de décomposition de A.

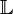Maintenant, χA(Z) = Z2 − X2 = (Z − X)2 n'est plus irréductible, et A a comme valeur propre double X. Si A était diagonalisable, elle serait semblable à la matrice scalaire XI, donc égale à cette matrice. Mais on constate que A n'est pas une matrice scalaire. Elle n'est donc pas diagonalisable et donc pas semi-simple sur \mathbb{L}.

Articles liés

Références

Jean-Marie Arnaudiès et José Bertin, Groupes, algèbres et géométrie, Ellipses (1993).

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Matrice semi-simple ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrices semi-simples de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Algèbres semi-simples — Algèbre semi simple En mathématiques et plus particulièrement en algèbre, une A algèbre L, où A désigne un anneau, est qualifiée de semi simple ou de complètement réductible si et seulement si la structure d anneau associé à L l est Elle est… …   Wikipédia en Français

  • Semi-simple — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs objets mathématiques sont qualifiés de semi simples : Les groupes semi simples ; Les modules semi simples ; Les algèbres semi… …   Wikipédia en Français

  • Anneau semi-simple — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques et plus particulièrement en algèbre, un anneau A est dit semi simple si A, considéré comme A module, est semi simple, c est à dire somme directe de A modules qui n admettent… …   Wikipédia en Français

  • Algebre semi-simple — Algèbre semi simple En mathématiques et plus particulièrement en algèbre, une A algèbre L, où A désigne un anneau, est qualifiée de semi simple ou de complètement réductible si et seulement si la structure d anneau associé à L l est Elle est… …   Wikipédia en Français

  • Algèbre Semi-simple — En mathématiques et plus particulièrement en algèbre, une A algèbre L, où A désigne un anneau, est qualifiée de semi simple ou de complètement réductible si et seulement si la structure d anneau associé à L l est Elle est présente dans de… …   Wikipédia en Français

  • Algèbre semi-simple — En mathématiques et plus particulièrement en algèbre, une A algèbre L, où A désigne un anneau, est qualifiée de semi simple ou de complètement réductible si et seulement si la structure d anneau associé à L l est Elle est présente dans de… …   Wikipédia en Français

  • Matrice semi-simple — En algèbre linéaire, la notion de matrice semi simple constitue une généralisation de la notion de matrice diagonalisable. Elle permet de discriminer deux types d obstruction à la diagonalisabilité : d une part les obstructions liées à l… …   Wikipédia en Français

  • GROUPES (mathématiques) - Groupes de Lie — La théorie des groupes de Lie, fondée dans la période de 1870 1880 par le mathématicien norvégien Sophus Lie, a d’abord été considérée comme une partie assez marginale des mathématiques, liée à des problèmes touchant les équations différentielles …   Encyclopédie Universelle

  • Groupe classique — En mathématiques, les groupes classiques sont différentes familles de groupes de transformations liées à l algèbre linéaire, principalement les groupes linéaires, orthogonaux, symplectiques et unitaires. Ces groupes peuvent aussi être présentés… …   Wikipédia en Français

  • Representations d'un groupe fini — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”