Matrices totalement unimodulaires

Matrices totalement unimodulaires

Matrice unimodulaire

Une matrice unimodulaire est une matrice carrée d'entiers avec un déterminant égal à -1 ou +1.

Sommaire

Exemple de matrices unimodulaires

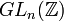Les matrices unimodulaires d'ordre n forment un groupe pour le produit. Leur ensemble se note GL_n(\mathbb{Z}).

Les matrices suivantes sont unimodulaires :

Matrice totalement unimodulaire

Une matrice totalement unimodulaire (TUM) est une matrice pour laquelle chaque sous-matrice carrée inversible est unimodulaire. Ces matrices n'ont pas besoin d'être carrée. On déduit de cette définition que les éléments d'une TUM peuvent uniquement être -1, 0 ou +1.

Exemple de matrice totalement unimodulaire

La matrice suivante est totalement unimodulaire :

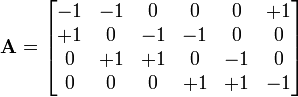
\mathbf{A}=\begin{bmatrix} -1 & -1 & 0 & 0 & 0 & +1\\ +1 & 0 & -1 & -1 & 0 & 0\\ 0 & +1 & +1 & 0 & -1 & 0\\ 0 & 0 & 0 & +1 & +1 & -1\\ \end{bmatrix}

Condition suffisante pour être totalement unimodulaire

Une condition suffisante mais pas nécessaire pour qu'une matrice A soit totalement unimodulaire :

Soit A une matrice m*n dont les lignes sont partitionnées en 2 ensembles disjoints B et C avec les propriétés suivantes :

  • Chaque colonne de A contient au plus 2 éléments non nuls
  • Chaque élément de A vaut -1, 0 ou +1
  • Si 2 éléments d'une colonne de A ont le même signe, alors la ligne de l'un est dans B, l'autre dans C
  • Si 2 éléments d'une colonne de A ont des signes opposés, alors les lignes des 2 éléments sont dans B ou toutes les 2 dans C

alors les déterminants des sous matrices de A sont -1, 0 ou +1.

Extension

La présentation ci-dessus utilise les nombres entiers relatifs. En algèbre abstraite, on étend la notion de matrice unimodulaire à tout anneau commutatif unitaire et intègre[1].

Références

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Matrice unimodulaire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrices totalement unimodulaires de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Theoreme de Konig (theorie des graphes) — Théorème de König (théorie des graphes) En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que toute arête… …   Wikipédia en Français

  • Théorème de König (théorie des graphes) — Pour les articles homonymes, voir Théorème de König. En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que …   Wikipédia en Français

  • Théorème de könig (théorie des graphes) — En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que toute arête de G est incidente à au moins un sommet… …   Wikipédia en Français

  • Matrice unimodulaire — En algèbre linéaire, une matrice unimodulaire sur l anneau des entiers relatifs est une matrice carrée à coefficients entiers dont le déterminant vaut +1 ou 1. Plus généralement[1], une matrice unimodulaire sur un anneau commutatif A est une… …   Wikipédia en Français

  • Forme Modulaire — En mathématiques, une forme modulaire est une fonction analytique sur le demi plan de Poincaré satisfaisant à une certaine sorte d équation fonctionnelle et de condition de croissance. La théorie des formes modulaires par conséquent est dans la… …   Wikipédia en Français

  • Forme modulaire — En mathématiques, une forme modulaire est une fonction analytique sur le demi plan de Poincaré satisfaisant à une certaine sorte d équation fonctionnelle et de condition de croissance. La théorie des formes modulaires par conséquent est dans la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”