Corps De Décomposition

En mathématiques et plus précisément en algèbre dans la théorie de Galois, le corps de décomposition d'un polynôme formel P(X) est la plus petite extension de corps contenant toutes les racines de P(X). On montre qu'une telle extension existe toujours.

Un corps de décomposition d'un polynôme est une extension finie et normale. S'il est séparable, c'est une extension de Galois.

Toute la théorie de Galois s'applique, un tel corps bénéficie de théorèmes puissants, comme le théorème de l'élément primitif ou le théorème fondamental de la théorie de Galois. De nombreux problèmes se résolvent alors à l'aide de cette structure. On peut citer par exemple le théorème d'Abel ou la détermination des polygones constructible à la règle et au compas.

Sommaire 1 Définition 2 Exemples 3 Propriétés 4 Voir aussi 4.1 Notes 4.2 Liens externes 4.3 Références

Définition

Les notations suivantes sont utilisées pour tout l'article, soit K un corps, P(X) un polynôme à coefficients dans K et Ω une clôture algébrique de K. Le polynôme P(X) désigne un polynôme formel, par opposition à une fonction polynôme, il est construit à l'aide d'une indéterminée noté X et non pas une variable x.

• Il existe une plus petite extension de corps L sur K telle que le polynôme P(X) soit scindé (c’est-à-dire qu'il soit le produit de polynômes du premier degré) sur L. Minimal signifie ici que toute sous-extension F de L contenant toutes les racines de P(X) est égale à L. Cette extension est appelée corps de décomposition de P(X).

• Soit (l₁, ..., l_n) une famille f d'éléments algébriques de Ω. Le plus petit corps de Ω contenant la famille et K est noté K(l₁, ..., l_n) et est appelé l'extension engendrée par la famille f.

L est isomorphe à un sous-corps de Ω, il est donc possible d'identifier L à un sous-corps de Ω comme le prouve le paragraphe Extension algébrique et clôture algébrique. Cette identification est réalisée dans le reste de l'article.

Si r₁, ..., r_n sont les racines de P(X) dans L, alors L s'identifie à K(r₁, ..., r_n). La démonstration de l'existence du corps de décomposition se trouve dans le paragraphe Extension algébrique et polynôme.

Remarque: Il existe une autre convention, le corps de décomposition d'un polynôme P(X) sur K désigne toute extension contenant toutes les racines de P(X), le corps minimal est alors appelé le corps des racines.

Exemples

Le corps de décomposition du polynôme X²+1 sur le corps des nombres réels est le corps des nombres complexes.

Construisons alors le corps de décomposition L du polynôme P(X) = X³ - 2 sur le corps des nombres rationnels. Soit r la racine cubique (réelle) de 2, et j la racine cubique (complexe) de l'unité ayant une composante imaginaire positive. Alors les deux autres racines sont j.r et j².r. Aucune racine n'est rationnelle, donc le polynôme est irréductible (en effet tout polynôme de degré trois qui n'est pas irréductible possède une racine rationnelle).

Considérons l'extension K₁ égale à Q(r), c’est-à-dire l'extension engendrée par r. Comme P(X) est irréductible, c'est une extension de degré trois isomorphe à Q[X]/(P(X)Q[X]) (cf le paragraphe Extension algébrique et polynôme) et dont une base est {1, r, r²}.

Sur K₁ le polynôme P(X) possède une racine r. Une division de P(X) par le polynôme X - r donne l'égalité:

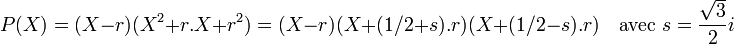
On en déduit que L est égal à K₁(s) qui est une extension de degré deux de K₁ et dont une base est {1, s}.

On a l'égalité sur les degrés [L:Q] =[L:K₁].[K₁:Q]= 3 x 2 = 6 (cf. Définitions et premières propriétés des extensions algèbriques). On en déduit une base de L sur K qui est {1, r, r²,s ,s.r, s.r²}.

Remarque: la méthode présentée ici est générique, elle peut être utilisée pour bâtir des corps de décomposition.

Propriétés

• Un corps de décomposition est une extension finie.

Cette propriété est démontrée dans le paragraphe Extension algébrique et sur-corps.

• Deux corps de décomposition de P(X) sur un corps K sont isomorphes comme extensions de K.

Cette propriété est démontrée dans le paragraphe Extension algébrique et sur-corps.

• Si un corps de décomposition est généré par des éléments séparables, alors il est séparable et le théorème de l'élément primitif s'applique. En conséquence, l'extension est séparable et simple.

• Si P(X) est irréductible et séparable, alors le corps de décomposition est galoisien: Soient r₁,...,r_n les racines de P(X) dans Ω. Alors L est égal à K(r₁,...,r_n). Tout morphisme de L dans Ω permute les racines, donc laisse stable L, ce qui montre que l'extension est normale. Comme L est une extension séparable et normale, elle est donc de Galois.

• On suppose le polynôme P(X) séparable, le groupe de Galois opère transitivement sur l'ensemble R des racines si, et seulement si, le polynôme est irréductible.^[1]

En effet, si P n'est pas irréductible, il existe deux polynômes P₁ et P₂ de degré strictement positif tel que P soit égal à P₁.P₂. Soient α (resp. β) une racine de P₁ (resp. P₂) et σ un élément du groupe de Galois. Le polynôme minimal de σ(α) est égal à P₁, celui de β à P₂, on en déduit que σ(α) ne peut être égal à β, ce qui revient à dire que le groupe n'opère pas transitivement.

Réciproquement si P est irréductible, soient α et β deux racines de P. Soit m le morphisme de K(α), dans K(β) qui à α associe β. L'avant dernière proposition du paragraphe Morphisme dans la clôture algébrique de l'article Extension séparable montre que le morphisme de corps m se prolonge en un automorphisme σ du corps de décomposition. Il existe ainsi un élément σ du groupe de Galois tel que σ(α) = β, ce qui montre que le groupe opère transitivement.

Voir aussi

Notes

Liens externes

• (fr) Une courte présentation des extensions algébriques par Bernard le Stum Université de Rennes 1 2001
• (fr) Un cours de DEA sur la théorie de Galois par Alain Kraus Université de Paris VI 1998
• (fr) Les correspondances de Galois dans les-mathématiques.net

Références

Adrien Douady et Régine Douady, Algèbre et théories galoisiennes [détail des éditions]

Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]

Pierre Samuel, Théorie algébrique des nombres [détail des éditions]

Articles de mathématiques en rapport avec la théorie de Galois
Corps	Corps fini · Corps parfait · Corps de rupture · Corps de décomposition
Extension de corps	Extension algébrique · Extension quadratique · Extension simple · Extension normale · Extension séparable · Extension de Galois · Groupe de Galois · Clôture algébrique
Articles associés	Caractéristique · Polynôme formel · Polynôme cyclotomique · Théorie de Galois · Théorème fondamental de la théorie de Galois · Théorème de l'élément primitif · Théorie d'Iwasawa

• Portail des mathématiques