Matrice échelonnée-réduite-ligne
- Matrice échelonnée-réduite-ligne
-
Matrice échelonnée
Une matrice est dite échelonnée, si le nombre de zéros précédant la première valeur non nulle d'une ligne augmente ligne par ligne jusqu'à ce qu'il ne reste plus que des zéros.
Voici un exemple de matrice échelonnée (les 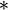 désignent des coefficients arbitraires, les
désignent des coefficients arbitraires, les 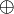 des pivots, coefficients non nuls)
des pivots, coefficients non nuls)

Un exemple de matrice échelonnée réduite ou matrice canonique en lignes (les pivots valent 1 et les autres coefficients dans les colonnes des pivots sont nuls)

Voir aussi
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
Algorithme d'échelonnement
 Portail des mathématiques
Portail des mathématiques
Catégorie : Matrice remarquable
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Matrice échelonnée-réduite-ligne de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice echelonnee — Matrice échelonnée Une matrice est dite échelonnée, si le nombre de zéros précédant la première valeur non nulle d une ligne augmente ligne par ligne jusqu à ce qu il ne reste plus que des zéros. Voici un exemple de matrice échelonnée (les… … Wikipédia en Français
Matrice Échelonnée — Une matrice est dite échelonnée, si le nombre de zéros précédant la première valeur non nulle d une ligne augmente ligne par ligne jusqu à ce qu il ne reste plus que des zéros. Voici un exemple de matrice échelonnée (les désignent des… … Wikipédia en Français
Matrice échelonnée — Une matrice est dite échelonnée en lignes si le nombre de zéros précédant la première valeur non nulle d une ligne augmente ligne par ligne jusqu à ce qu il ne reste plus que des zéros. Voici un exemple de matrice échelonnée (les désignent des… … Wikipédia en Français
Forme échelonnée réduite — Matrice échelonnée Une matrice est dite échelonnée, si le nombre de zéros précédant la première valeur non nulle d une ligne augmente ligne par ligne jusqu à ce qu il ne reste plus que des zéros. Voici un exemple de matrice échelonnée (les… … Wikipédia en Français
Rang (Matrice) — Rang (mathématiques) Pour les articles homonymes, voir Rang. En algèbre linéaire, le rang d une famille de vecteurs est la dimension du sous espace vectoriel engendré par cette famille. On peut étendre la notion de rang aux matrices et aux… … Wikipédia en Français
Rang (matrice) — Rang (mathématiques) Pour les articles homonymes, voir Rang. En algèbre linéaire, le rang d une famille de vecteurs est la dimension du sous espace vectoriel engendré par cette famille. On peut étendre la notion de rang aux matrices et aux… … Wikipédia en Français
Rang D'une Matrice — Rang (mathématiques) Pour les articles homonymes, voir Rang. En algèbre linéaire, le rang d une famille de vecteurs est la dimension du sous espace vectoriel engendré par cette famille. On peut étendre la notion de rang aux matrices et aux… … Wikipédia en Français
Rang d'une matrice — Rang (mathématiques) Pour les articles homonymes, voir Rang. En algèbre linéaire, le rang d une famille de vecteurs est la dimension du sous espace vectoriel engendré par cette famille. On peut étendre la notion de rang aux matrices et aux… … Wikipédia en Français
Operation elementaire — Opération élémentaire En algèbre linéaire, les opérations élémentaires sur une famille de vecteurs sont des manipulations algébriques qui ne modifient pas les propriétés d indépendance linéaire, ni le sous espace vectoriel engendré. Elles sont… … Wikipédia en Français
Opération élémentaire — En algèbre linéaire, les opérations élémentaires sur une famille de vecteurs sont des manipulations algébriques qui ne modifient pas les propriétés d indépendance linéaire, ni le sous espace vectoriel engendré. Elles sont faciles à décrire sous… … Wikipédia en Français
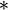 désignent des coefficients arbitraires, les
désignent des coefficients arbitraires, les 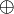 des pivots, coefficients non nuls)
des pivots, coefficients non nuls)

