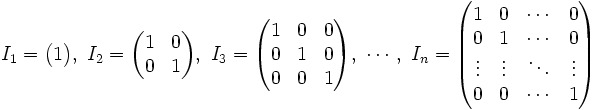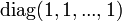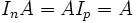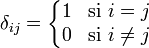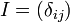Matrice identité

Matrice identité

Matrice unité

En algèbre linéaire, la matrice unité ou matrice identité (cette dernière dénomination étant un anglicisme) est une matrice carrée avec des 1 sur la diagonale et des 0 partout ailleurs. Nous pouvons l'écrire

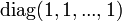
{\displaystyle \rm diag}(1,1,...,1)

Puisque les matrices peuvent être multipliées à la seule condition que leurs types soient compatibles, il y a des matrices unité de tout ordre. In, est la matrice unité d'ordre n est donc définie comme une matrice diagonale avec 1 sur chaque entrée de sa diagonale principale. Ainsi :

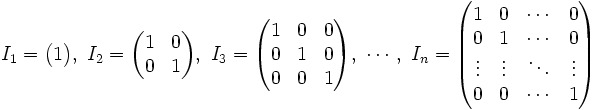
I_1 = \begin{pmatrix} 1 \end{pmatrix} ,\ I_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} ,\ I_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} ,\ \cdots ,\ I_n = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}

Concernant la multiplication des matrices, les matrices unités vérifient que pour tous p, n entiers naturels non nuls et pour toute matrice A à n lignes et p colonnes,

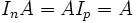
I_n A = A I_p =A \,

Ce qui montre que la multiplication par une matrice unité n'a aucun effet sur une matrice donnée.

En particulier si n=p, In est l'élément neutre pour la multiplication des matrices carrées d'ordre n.


Il est possible aussi de noter les coefficients de la matrice unité d'ordre n avec le symbole de Kronecker ; le coefficient de la i-ème ligne et j-ème colonne s'écrit :

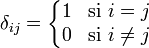
\delta_{ij} = \left\{\begin{matrix} 1 & \mbox{si } i=j \\ 0 & \mbox{si } i \ne j \end{matrix}\right.\,

et donc la matrice unité I est égale à

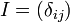
I = (\delta_{ij}) \,

Si l'ordre n'est pas précisé, ou qu'il est trivialement déterminé par le contexte, nous pouvons la noter simplement I.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Matrice unit%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice identité de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Matrice Identité — Matrice unité En algèbre linéaire, la matrice unité ou matrice identité (cette dernière dénomination étant un anglicisme) est une matrice carrée avec des 1 sur la diagonale et des 0 partout ailleurs. Nous pouvons l écrire Puisque les matrices… …   Wikipédia en Français

  • Matrice identite — Matrice unité En algèbre linéaire, la matrice unité ou matrice identité (cette dernière dénomination étant un anglicisme) est une matrice carrée avec des 1 sur la diagonale et des 0 partout ailleurs. Nous pouvons l écrire Puisque les matrices… …   Wikipédia en Français

  • Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice Symplectique — En mathématique, une matrice symplectique est une matrice M de taille 2n par 2n (dont les entrées sont typiquement soit des réels soit des complexes) satisfaisant la condition MTJM = J où MT désigne la transposition de M et J est la matrice… …   Wikipédia en Français

  • Matrice symplétique — Matrice symplectique En mathématique, une matrice symplectique est une matrice M de taille 2n par 2n (dont les entrées sont typiquement soit des réels soit des complexes) satisfaisant la condition MTJM = J où MT désigne la transposition de M et J …   Wikipédia en Français

  • Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D …   Wikipédia en Français

  • Matrice Diagonale — En algèbre linéaire, une matrice diagonale est une matrice carrée dont les coefficients en dehors de la diagonale principale sont nuls. Les coefficients de la diagonale peuvent être ou ne pas être nuls. Ainsi, la matrice D = (di,j) est diagonale… …   Wikipédia en Français

  • Matrice scalaire — Matrice diagonale En algèbre linéaire, une matrice diagonale est une matrice carrée dont les coefficients en dehors de la diagonale principale sont nuls. Les coefficients de la diagonale peuvent être ou ne pas être nuls. Ainsi, la matrice D = (di …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”