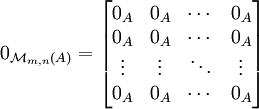
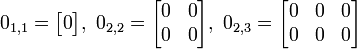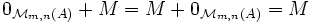Matrice Nulle
- Matrice Nulle
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Matrice Nulle de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice nulle — ● Matrice nulle matrice dont tous les éléments sont égaux à zéro … Encyclopédie Universelle
Matrice nulle — En mathématiques, et en particulier en algèbre linéaire, une matrice nulle est une matrice dont tous les coefficients sont nuls. Des exemples de matrices nulles sont: L ensemble des matrices de dimension à coefficients dans un anneau A forme un… … Wikipédia en Français
Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D … Wikipédia en Français
Matrice Nilpotente — Une matrice nilpotente est une matrice dont il existe une puissance égale à la matrice nulle. Elle correspond à la notion d endomorphisme nilpotent. Cette notion joue un rôle important dans le monde des matrices. En effet, pour un maniement plus… … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice par blocs — Matrice par bloc En théorie des matrices, une matrice par bloc ou matrice partitionnée est une matrice pouvant être divisée en matrices rectangulaires de dimensions inférieures appelées blocs. On peut dire également que la matrice est écrite en… … Wikipédia en Français
Matrice Identité — Matrice unité En algèbre linéaire, la matrice unité ou matrice identité (cette dernière dénomination étant un anglicisme) est une matrice carrée avec des 1 sur la diagonale et des 0 partout ailleurs. Nous pouvons l écrire Puisque les matrices… … Wikipédia en Français
Matrice identite — Matrice unité En algèbre linéaire, la matrice unité ou matrice identité (cette dernière dénomination étant un anglicisme) est une matrice carrée avec des 1 sur la diagonale et des 0 partout ailleurs. Nous pouvons l écrire Puisque les matrices… … Wikipédia en Français
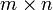 à coefficients dans un anneau A forme un anneau
à coefficients dans un anneau A forme un anneau 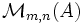 . La matrice nulle
. La matrice nulle 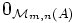 , dans
, dans 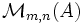 est la matrice ayant tous les coefficients égaux à
est la matrice ayant tous les coefficients égaux à 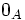 , où
, où 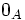 est l'élément neutre additif de A.
est l'élément neutre additif de A.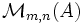 . Cela signifie que pour toute matrice
. Cela signifie que pour toute matrice 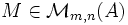 on a
on a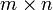 ayant des coefficients dans un anneau donné, ainsi lorsque le contexte apparaît clairement 0 désigne la matrice nulle. En général l'élément zéro d'un anneau est unique et est noté typiquement 0 sans aucun indice indiquant l'anneau le contenant. Ainsi les exemples précédents représentent les matrices nulles sur n'importe quel anneau.
ayant des coefficients dans un anneau donné, ainsi lorsque le contexte apparaît clairement 0 désigne la matrice nulle. En général l'élément zéro d'un anneau est unique et est noté typiquement 0 sans aucun indice indiquant l'anneau le contenant. Ainsi les exemples précédents représentent les matrices nulles sur n'importe quel anneau.