Anneau euclidien

Euclide (Juste de Gand, vers 1474)

En mathématiques et plus précisément en algèbre, dans le cadre de la théorie des anneaux, un anneau euclidien est un type particulier d'anneau intègre.

Un anneau est dit euclidien s'il est possible d'y définir une division euclidienne.

Cette propriété est riche de conséquences : un anneau euclidien est toujours principal, il vérifie l'identité de Bézout, le lemme d'Euclide, il est factoriel et satisfait les conditions du théorème fondamental de l'arithmétique. On retrouve ainsi tous les résultats de l'arithmétique élémentaire et plus spécifiquement de l'arithmétique modulaire, mais dans un cadre plus général.

L'anneau euclidien le plus classique est celui des entiers, mais on trouve aussi celui des entiers de Gauss ou encore un autre anneau, permettant de bâtir une arithmétique liée au nombre d'or et explicative de nombreuses propriétés de cet irrationnel. L'anneau des polynômes à coefficients dans les nombres réels ou complexes, et plus généralement dans n'importe quel corps commutatif est aussi euclidien, donnant ainsi naissance à une arithmétique des polynômes.

Sommaire

1 Histoire
2 Exemples
3 Définitions
4 Propriétés
- 4.1 Propriétés des anneaux euclidiens
- 4.2 Propriétés des stathmes
5 Notes et références
- 5.1 Notes
- 5.2 Références
6 Voir aussi
- 6.1 Liens externes
- 6.2 Articles connexes

Histoire

Couverture de la première édition anglaise des Éléments par Henry Billingsley, 1570

Origine

La première référence ayant influencé le monde mathématique sur la question de la division euclidienne est le livre VII^[1], des Éléments d'Euclide datant d'environ 300 ans avant J.-C.. On y trouve la première définition théorique de la division et l'étude de ses conséquences. Cette branche des mathématiques prend le nom d'Arithmétique. Elle traite essentiellement des questions portant sur les nombres entiers.

Certains mathématiciens comme Diophante d'Alexandrie^[2] puis, bien plus tard, Pierre de Fermat^[3] comprennent la richesse de cette branche des mathématiques. Ils établissent quelques résultats comme le petit théorème de Fermat et formulent des conjectures comme le théorème des deux carrés de Fermat ou le grand théorème de Fermat. Un outil théorique important est l'analyse des propriétés du reste de la division euclidienne des membres d'une égalité d'entiers. Au XVIII^e siècle, certaines conjecture sont démontrées. On peut citer Leonhard Euler^[4] avec le théorème des deux carrés ou le cas n égal à trois du grand théorème de Fermat, presque traité en 1753. D'autres conjectures comme celle de la loi de réciprocité quadratique apparaissent. Ces résultats sont pour l'essentiel démontrés grâce à la virtuosité des mathématiciens, mais l'apport théorique est faible, en conséquence les résultats sont peu généralisables.

Émergence du concept

Carl Friedrich Gauss

En 1801, Carl Friedrich Gauss^[5] étudie le premier anneau d'entiers algébriques, celui des entiers qui portent maintenant son nom. Cet anneau possède l'équivalent d'une division euclidienne dans Z. En conséquence, l'identité de Bézout, le lemme d'Euclide, et le théorème fondamental de l'arithmétique s'appliquent. De même, l'anneau des polynômes à coefficients dans un corps commutatif, dispose aussi d'une division euclidienne. Gauss y construit une arithmétique analogue aux précédentes. Ainsi, la division euclidienne n'apparaît plus comme une spécificité des nombres relatifs mais un algorithme qui s'applique à diverses ensembles munis d'une multiplication et d'une addition.

Cette approche est utilisée pour d'autres entiers algébriques, par exemple par Gotthold Eisenstein^[6] qui découvre l'ensemble des nombres appelés entiers d'Eisenstein et qui dispose d'une division euclidienne.

L'apport d'une division euclidienne à une structure est une démarche féconde. Gauss s'en sert pour une de ses démonstrations de la loi de réciprocité quadratique et des progrès tangibles sont réalisés vers la résolution du grand théorème de Fermat. Le cas particulier de ce théorème où l'exposant est 3 est prouvé de façon parfaitement rigoureuse. Les cas d'un exposant 5, puis 14, puis 7, sont démontrés, avec l'apport massif d'autres idées. L'application de la décomposition en facteurs premiers aux polynômes cyclotomiques permet à Gauss de trouver une nouvelle construction à la règle et au compas d'un polygone régulier, l'heptadécagone ou polygone régulier à 17 côtés.

L'idée est suffisamment novatrice et fructueuse pour que le lemme d'Euclide et le théorème fondamental de l'arithmétique soient parfois rebaptisés lemme de Gauss et théorème de Gauss. Le livre d'arithmétique de Gauss vaut rapidement à son auteur, le surnom de prince des mathématiciens.

Formalisation

Paradoxalement la formalisation moderne provient des limitations des arithmétiques précédentes. Par une démarche utilisant la notion d'anneau d'entiers, Gabriel Lamé pense qu'il a démontré le grand théorème de Fermat^[7]. Ernst Kummer montre par un exemple^[8] en 1844 qu'un anneau d'entiers ne dispose pas, en général, d'une décomposition unique en facteurs premiers. Ce résultat invalide la preuve de Lamé. Kummer découvre en 1846 un nouveau concept qu'il baptise nombre complexe idéal pour retrouver sous une nouvelle forme l'unicité nécessaire.

Ces travaux ouvrent la voie à la formalisation de la structure d'anneau. On peut citer Richard Dedekind^[9] et David Hilbert^[10] parmi les principaux contributeurs. Un anneau euclidien devient un cas particulier simple d'une vaste théorie, la théorie des anneaux. Dans ce contexte, l'anneau euclidien est un cas spécifique d'anneau intègre. Il entre dans la sous-famille des anneaux factoriels et plus précisément des anneaux principaux, un cas particulier d'anneau factoriel. Les anneaux d'entiers étudiés par Kummer entrent dans une famille différente, celle des anneaux de Dedekind.

Exemples

Entiers relatifs

Article détaillé : arithmétique élémentaire.

Illustration de l'irrationalité de √2.

Les entiers relatifs forment le prototype de l'anneau euclidien. Cet ensemble vérifie la propriété suivante :

$\forall a\in\Z,\forall b\in\Z^*, \exists q, r\in\Z\quad / \quad a=bq+r \quad {\rm et } \quad |r| < |b|$ .

On reconnait là la forme de la division euclidienne dans l'ensemble des entiers naturels N pour laquelle |n| = n. On peut remarquer toutefois que, d'une part N n'est pas un anneau, d'autre part il n'est pas précisé ici l'unicité de q et r. Ceci s'explique par le fait que, pour pouvoir prolonger à Z (ensemble des entiers relatifs) la définition de la division dans N, il faut, ou bien fixer une condition supplémentaire sur b (b > 0) restreignant ainsi le champ de validité de la division euclidienne, ou bien accepter de prendre b négatif et prendre pour définition a = bq + r avec |r| < |b|. Mais alors on peut trouver deux décompositions possibles :

19 = (- 5) × (- 3) + 4 avec |4| < |-5| mais aussi 19 =(- 5) × (- 4) + (-1) avec |-1| < |-5|.

Cette division permet de bâtir une arithmétique vérifiant les propriétés suivantes :

tout idéal de l'anneau des entiers est principal, c'est-à-dire qu'il est de la forme n.Z pour un certain élément n de Z. Un anneau dont tous les idéaux sont principaux est dit principal ;
l'identité de Bézout est vérifiée ;
le lemme d'Euclide est vérifiée ;
le théorème fondamental de l'arithmétique s'applique.

En conséquence, il est possible de définir : la famille des nombres premiers, le ppcm ainsi que le pgcd. L'anneau quotient Z/nZ est bien défini, il est la structure à la base de l'arithmétique modulaire.

La première application connue est probablement la démonstration de l'irrationalité de la racine carrée de deux. Le petit théorème de Fermat se démontre rapidement une fois établi le fait que si n est premier Z/nZ dispose d'une structure de corps. Fermat utilise largement cette arithmétique, par exemple pour démontrer l'absence de solution pour son grand théorème si n est égal à quatre. Euler donne une large quantité d'exemples d'utilisation de l'arithmétique dans Z, comme l'étude de l'équation de Pell-Fermat.

Ces résultats sont les propriétés qui ont motivé la création de la notion abstraite d'anneau euclidien. En effet, toutes ces propriétés ne sont les conséquences que d'une seule, la division euclidienne.

Polynômes à coefficients dans un corps commutatif

Article détaillé : Division d'un polynôme.

Évariste Galois initiateur de la théorie portant son nom

Construction d'un pentagone

Si K est un corps commutatif, alors l'anneau des polynômes K[X] est euclidien. La division prend la forme suivante :

$\forall A(X)\in K[X],\quad\forall B(X)\in K[X]\setminus\{0\},\quad \exists ! Q(X), R(X)\in K[X]$ $\text{tel que} \quad A(X)=B(X)Q(X)+R(X)\quad\text{et} \quad \text{deg} R(X) < \text{deg} B(X)$ .

Si la forme est globalement analogue à celle des entiers, on remarque néanmoins qu'une relation d'ordre sur l'ensemble K[X] n'est pas nécessaire. Il suffit d'une application, analogue à celle qui, à un polynôme associe son degré, et dont l'ensemble d'arrivée est ordonné, une telle application est appelée stathme euclidien.

L'arithmétique se fonde sur les mêmes conséquences, l'anneau est principal, l'identité de Bézout est vérifiée, le lemme d'Euclide et le théorème fondamental de l'arithmétique s'appliquent. Les équivalents des nombres premiers sont les polynômes irréductibles, c’est-à-dire ceux qui n'ont pour diviseurs qu'eux-mêmes ou l'unité à une constante multiplicative près. La décomposition en polynômes irréductibles est la factorisation la plus complète possible.

L'équivalent de l'arithmétique modulaire se focalise sur les anneaux quotientés par des idéaux premiers (c’est-à-dire des idéaux engendrés par des polynômes irréductibles). Comme précédemment ces idéaux possèdent une structure de corps. Les quotients sont appelés corps de rupture car se sont les plus petits corps contenant une racine du polynôme. Cette approche, permettant de définir une extension finie du corps K définit l'outil de base de la théorie de Galois.

Un exemple d'application est le suivant : les polynômes cyclotomiques correspondent à la décomposition en facteurs irréductibles du polynôme des racines de l'unité Xⁿ - 1. L'analyse de ces polynômes permet de déterminer tous les polygones constructibles à la règle et au compas.

Entiers de Gauss

Article détaillé : Entier de Gauss.

Les entiers de Gauss noté Z[i] correspondent aux nombres de la forme u + i.v ou u et v sont choisis entiers. Ils forment un anneau euclidien, la définition est donnée par la proposition suivante, si N(x) désigne la norme algébrique c’est-à-dire le carré du module de x :

$\forall a\in\Z(i),\forall b\in\Z(i)^*,\qquad\exists q, r\in\Z(i)\quad / \quad a=b.q+r \quad\text{avec}\quad N(r) < N(b)$ .

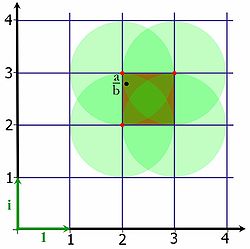
L'application qui à un entier associe sa norme algébrique est bien une application des entiers de Gauss dans un ensemble ordonné, à savoir celui des entiers positifs. Cette norme correspond graphiquement au carré de la distance entre l'origine et l'entier de Gauss.

Dire que la division euclidienne existe signifie que qu'il existe un entier de Gauss à une distance inférieure à 1 du nombre complexe a/b. La figure ci-jointe illustre par un fond rouge le carré de sommet des entiers de Gauss et contenant a/b. La figure montre qu'il existe toujours au moins un entier à une distance inférieure à 1 de a/b. Dans le cas illustré, il en existe trois vérifiant cette propriété. L'unicité de la solution n'est pas une condition nécessaire à l'existence d'une division euclidienne.

Une fois encore, la division euclidienne apporte une arithmétique analogue aux deux cas précédents.

Les applications sont nombreuses. Dedekind a, par exemple, trouvé une preuve élégante du théorème des deux carrés de Fermat à partir de cet ensemble. Certaines équations diophantiennes quadratiques se résolvent bien dans cet ensemble. Gauss a utilisé cette arithmétique pour démontrer la loi de réciprocité quadratique.

En règle générale, un ensemble de cette nature, appelé anneau d'entiers quadratiques, n'a pas de division euclidienne. Ainsi, Z[i√3] n'est pas euclidien.

Autres anneaux euclidiens

Il existe d'autres anneaux d'entiers quadratiques euclidiens. Ceux qui ne sont pas inclus dans R sont tous connus. Les autres, comme par exemple celui des entiers de Q(√5), sont dits totalement réels. (Appliquées à des corps quadratiques, les notions de réel et de totalement réel sont équivalentes.) Il est conjecturé qu'il existe une infinité d'anneaux quadratiques totalement réels euclidiens.
Si K est un corps commutatif, l'anneau K[[X]] de ses séries formelles est aussi euclidien, pour la valuation : v(P) = plus petit degré de X dans P.
Si A est un anneau euclidien et si S est une partie de A stable pour la multiplication, le localisé de A par rapport à S est aussi un anneau euclidien.

Définitions

Il existe certains points communs entre les exemples : l'anneau est toujours intègre et, dans chaque cas, une fonction à valeurs dans N (valeur absolue, degré ou norme) est utilisée pour définir la division euclidienne. Ces fonctions sont des cas particuliers de stathme euclidien. De façon générale, si A désigne un anneau intègre, on pose la définition suivante.

Un stathme euclidien sur A est une application v de A \ {0} dans l'ensemble N des entiers positifs vérifiant les deux propriétés^[11] :

$(1)\quad \forall a\in A,\forall b\in A\setminus\{ 0 \},\quad\exists q,r\in A \quad / \quad a = b.q + r \quad \text{avec} \quad r = 0 \;\, \text{ou}\; v(r) < v(b)$ ,

$(2)\quad \forall a, b \in A\setminus\{0 \} \quad v(b) \leq v(ab)$ .

La condition (2) revient à dire que si A \ {0} est muni de la relation de préordre «divise» et N de la relation d'ordre usuelle, l'application v est croissante.

Le terme de préstathme euclidien désigne une application de A \ {0} dans N possédant la propriété (1).

Un anneau intègre est dit euclidien si et seulement s'il existe un stathme euclidien sur cet anneau. On parle alors de division euclidienne dans cet anneau par rapport au stathme.

Remarques

Certains auteurs utilisent le terme de stathme euclidien pour désigner ce qui est appelé ici un préstathme^[12]. La différence n'est pas grande, car s'il existe un préstathme sur A, il existe aussi un stathme.

Démonstration

Soit A un anneau intègre muni d'un préstathme v, il existe un stathme w :

Par hypothèse, il existe un préstathme v sur A. Nous allons définir un stathme w. Pour tout élément non nul x de A, désignons par w(x) la plus petite des valeurs v(y), y parcourant les multiples non nuls de x. Puisque x est lui-même un tel y, nous avons :

$w(x) \leq v(x)$ .

Soient a et b deux éléments non nuls de A tels que b divise a, alors w(a) est supérieur ou égal à w(b) :

Soient E_a l'ensemble des valeurs v(a') où a' parcourt les multiples non nuls de a et E_b l'ensemble des valeurs v(b') où b' parcourt les multiples non nuls de b. La valeur w(a) est, par définition, le plus petit élément de w(E_a) et w(b) le plus petit élément de w(E_b). Puisque a est multiple de b, l'ensemble E_a est contenu dans l'ensemble E_b, donc inf(E_a), c'est-à-dire w(a), est supérieur ou égal à inf(E_b), c'est-à-dire à w(b).

La fonction w est un stathme, c'est-à-dire qu'elle vérifie aussi la condition :

$\forall a\in A,\forall b\in A\setminus\{ 0 \},\quad\exists q,r\in A \quad / \quad a = b.q + r \quad\text{avec}\quad r = 0 \quad\text{ou}\quad w(r) < w(b)$ .

Par définition de w, il existe un élément non nul c₀ de A tel que w(b) = v(bc₀).
Puisque v est un préstathme, la division euclidienne de a par bc₀ relativement à v fournit un couple (q ₀, r₀ ) d'éléments de A tels que :

$a = bc_{0}.q_{0} + r_{0} \quad\text{avec}\quad r_{0} = 0 \quad\text{ou}\quad v(r_{0}) < v(bc_{0})$ .

Si r₀ est nul, notre thèse est évidemment vraie (avec q = c₀q₀ et r= 0). Supposons donc r₀ non nul. Alors v(r₀) est strictement inférieur à v(bc₀). Nous avons vu que la fonction w est inférieure ou égale à v, donc w(r₀) est inférieur ou égal à v(r₀), donc

$w(r_{0}) \leq v(r_{0}) < v(bc_{0})$ ;

d'autre part, c₀ est choisi tel que w(b) = v(bc₀), donc

$w(r_{0}) \leq v(r_{0}) < v(bc_{0}) = w(b)$ ,

d'où w(r₀) < w(b).
Nous avons obtenu ainsi une « division de a par b » euclidienne par rapport à w, avec pour quotient c₀.q ₀ et pour reste r₀, ce qui achève de prouver notre thèse.

Comme le montrent des exemples donnés dans les cas particuliers introductifs, les éléments q et r de la relation (1) ne sont pas forcément uniques.

Propriétés

Propriétés des anneaux euclidiens

Articles détaillés : Anneau principal et Anneau factoriel.

Dans la suite de l'article, A est un anneau intègre.

Un anneau euclidien est principal.

Plus précisément, si v est un préstathme sur l'anneau euclidien A, si J est un idéal non nul de A, J admet pour générateur tout élément de J \ {0} dont la valeur par le préstathme v est minimale.

Démonstration

Soit b un élément de J \ {0} dont la valeur par v est minimale. Prouvons que b est un générateur de J. Soit a un élément de J. Il s'agit de prouver que a est multiple de b. Puisque v est un préstathme euclidien, il existe des éléments q et r de A tels que

$a = b.q + r \quad\text{avec}\quad r = 0\quad\text{ou}\quad v(r) < v(b)$ .

Puisque a et b sont tous deux des éléments de J, r en est un aussi ; si r n'était pas nul, on aurait donc $r \in J\setminus\{0\}$ et $v (r) < v (b)$ , ce qui contredit la minimalité de b. Donc r est nul, donc a est multiple de b comme annoncé.

En revanche, un anneau principal n'est pas toujours euclidien, l'article Anneau principal présente un contre-exemple.

Un anneau euclidien possède toutes les propriétés de divisibilité des anneaux principaux : il est factoriel, le lemme d'Euclide, le théorème fondamental de l'arithmétique et l'identité de Bézout sont vérifiés et les opérations sur le plus grand commun diviseur et le plus petit commun multiple s'appliquent.

Si on dispose d'un algorithme effectif de division euclidienne, comme par exemple pour Z ou pour les polynômes à coefficients dans un corps, on peut définir des algorithmes effectifs fournissant explicitement des objets dont l'existence reste théorique dans un cadre plus général. Ainsi l'algorithme d'Euclide se généralise et permet de trouver un générateur de la somme de deux idéaux (autrement dit, permet de trouver un plus grand commun diviseur de deux éléments). De même, le théorème des facteurs invariants permet de trouver une base d'un A-module de type fini.

Remarque : Pour prouver qu'un anneau euclidien est principal, nous avons seulement utilisé l'existence d'un préstathme et non celle d'un stathme, ce qui explique que certains auteurs ne s'intéressent qu'aux préstathmes (qu'ils appellent stathmes)^[13]. Toutefois, la preuve du fait qu'un anneau principal est factoriel repose (quant à l'existence de la décomposition en produits d'éléments irréductibles) sur l'axiome du choix dépendant. Dans le cas d'un anneau euclidien, l'existence d'un stathme permet de prouver que l'anneau est factoriel sans recours à cet axiome.

Démonstration

Tout anneau euclidien est factoriel :

Soit A un anneau euclidien; choisissons un stathme v sur A. On démontrera d'abord par récurrence sur v(x) que tout x non nul et non inversiblepossède au moins une décomposion en produit d'éléments irréductibles. Si x est lui même irréductible on prend x comme produit à un seul facteur. Sinon on peut écrire x = ab avec a et b non inversibles. On aura alors v(a) < v(x) et v(b) < v(x), donc on peut appliquer l'hypothèse de récurrence à a et b pour en fournir de factorisation, qu'on combine en une factorisation de x. La démonstration de l'unicité de cette factorisation (à l'ordre et à l'association près) est la même qui s'applique dans le cas général des anneaux principaux, donnée dans l'article sur les anneaux factoriels.

Propriétés des stathmes

Soient a et b deux éléments non nuls de A et v un stathme ; si v(a.b) = v(a), alors b est un élément du groupe des unités.

Démonstration

Il revient au même de prouver que si x et y sont des éléments non nuls de A, si x est diviseur strict de y (c'est-à-dire si x divise y sans en être multiple, autrement dit si y est de la forme xz avec z non inversible), alors v(x) < v(y).

Il existe q et r dans A tels que

$x = y.q + r \quad\text{avec}\quad r = 0\quad\text{ou}\quad v(r) < v(y)$ .

Puisque x est diviseur strict de y, il n'en est pas multiple, donc r n'est pas nul, donc v(r ) < v(y). Mais r est clairement multiple de x, donc, puisque nous supposons v croissant, v(x) ≤ v(r). Ainsi, v(x) ≤ v(r) < v(y), donc v(x) < v(y) comme annoncé.

Il est toujours possible de normaliser un stathme v par translation, c'est-à-dire de choisir un stathme w tel que l'image par le stathme d'une unité soit égal à un. Plus précisément, il suffit de définir w par w(x) = v(x) - v(1) + 1 pour tout élément non nul x de A. Dans ce cas :

Un élément non nul u de A est élément du groupe des unités de A si, et seulement si, w(u) = 1. De plus, 1 est la valeur minimale que prend w dans A \ {0}.

Si on étend le stathme normalisé w à l'anneau A tout entier en posant w(0) = 0, 0 est le seul élément x de A tel que w(x) = 0, ce qui permet de donner au principe de division euclidienne cette forme un peu plus élégante :

$\forall a\in A,\forall b\in A\setminus\{ 0 \},\quad\exists q,r\in A \quad / \quad a = b.q + r \quad\text{avec}\quad w(r) < w(b)$ .

Cette convention n'est pas suivie dans tous les cas. Le stathme dispose de propriétés qui dépassent souvent celles de la division euclidienne. Dans le premier exemple sur Z, le stathme dispose de propriétés métriques, dans le deuxième exemple la fonction degré vérifie une propriété utile : le degré du produit de deux polynômes est égal à la somme des degrés des polynômes. Pour ne pas perdre cette propriété, les unités de l'anneau ont un stathme (degré) choisi égal à zéro et le polynôme nul a pour image (degré) moins l'infini.

Notes et références

Notes

↑ Euclide, Les quinze livres des éléments géométriques d'Euclide : plus le livre des donnez du mesme Euclide aussi traduict en françois par ledit Henrion, et imprimé de son vivant, traduction de 1632, site Gallica
↑ Diophante d'Alexandrie, Arithmetica, éd. et tr. Roshdi Rashed, Paris : les Belles Lettres, 1984
↑ Pierre de Fermat, Œuvres de Fermat, publiées par Paul Tannery et Charles Henry
↑ Leonhard Euler, Opera mathematica, volume 3, 1771
↑ Carl Friedrich Gauss, Recherches arithmétiques, traduction A.-C.-M. Poullet-Delisle, 1801, traduction 1807, réimpr. 1989 Éditions Jacques Gabay
↑ Gotthold Eisenstein, Formes quadratiques et cubiques, Journal de Crelle, 1844
↑ Gabriel Lamé, Démonstration générale du théorème de Fermat, sur l'impossibilité, en nombres entiers, de l'équation xⁿ +yⁿ =zⁿ, CRAS 24 (1847), 310-315 Lire sur Gallica
↑ (en) Harold Edwards, The background of Kummer's proof of Fermat's Last Theorem for regular primes, Arch. History Exact Sci. 14 (1975)
↑ (de) Heinrich Weber, Lehrbuch der Algebra, 1871
↑ David Hilbert, Rapport sur les nombres, 1897
↑ Par exemple (Bourbaki 1973). Voir aussi (Dress 1970) (où la notion de stathme est plus générale : l'ensemble d'arrivée est un ordinal quelconque et non forcément N).
↑ On peut citer par exemple (Perrin 2004). Pour différentes définitions du stathme, voir encore (Dress 1970), (Bourbaki 1973), (Goblot 1997).
↑ (Perrin 2004), (Goblot 1997)

Références

(en) Theodore Motzkin, « The Euclidean algorithm », dans Bulletin of the American Mathematical Society, vol. 55, n^o 12, 1949, p. 1142-1146 [texte intégral]
Serge Lang, Algèbre [détail des éditions]
Daniel Perrin, Cours d'algèbre [détail des éditions], p. 50 , déf. 3.28
Saunders Mac Lane et Garrett Birkhoff, Algèbre [détail des éditions]
Bourbaki, Éléments de mathématique, Algèbre, 1973, chap. 7, § 1, p. 125 , exerc. 7
F. Dress, « Stathmes euclidiens et séries formelles », dans Séminaire Delange-Pisot-Poitou. Théorie des nombres, vol. 12, 1970, p. 1-7 [texte intégral]
R. Goblot, Algèbre commutative, Masson, 1997, p. 23

Voir aussi

Liens externes

(en) John J. O’Connor et Edmund F. Robertson, « Index for the Chronology », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne] .
Les-mathématiques.net Attention l'article contient une définition différente
Anneau et corps par Christian Squarcini
(en) Integral Domains, Euclidean Domains sur mathreference.com
(en) Euclidean domain sur planetmath.org

Articles connexes

v · Théorie des anneaux

Anneau unitaire • Anneau commutatif • Corps des fractions • Idéal • Anneau principal • Anneau euclidien • Anneau factoriel • Anneau noethérien • Anneau artinien • Algèbre sur un anneau • Module • Module monogène • Module libre • Facteur direct • Module quotient • Dual d'un module • Annulateur • Produit tensoriel • Puissance extérieure • Bimodule • Module simple • Module semi-simple • Longueur d'un module • Module projectif • Module injectif • Module plat • Module fidèle • Module artinien

Portail des mathématiques

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Anneau euclidien de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Anneau Euclidien — Euclide (Juste de Gand ,vers 1474) En mathématiques et plus précisément en algèbre, dans le cadre de la théorie des anneaux, un anneau euclidien est un type particulier d anneau commutatif unitaire intègre. Un anneau est dit euclidien s il est… … Wikipédia en Français
Anneau Principal — Les anneaux principaux forment un type d anneaux important dans la théorie mathématique de la divisibilité. Ce sont les anneaux intègres (commutatifs unitaires non nuls) auxquels on peut étendre deux théorèmes qui, au sens strict, concernent l… … Wikipédia en Français
Anneau (Mathématiques) — Pour les articles homonymes, voir Anneau. En algèbre générale, un anneau est une structure algébrique sur laquelle deux opérations satisfont certaines des propriétés de l addition et la multiplication des nombres. Sommaire 1 Aspect historique … Wikipédia en Français
Anneau Factoriel — En mathématiques, un anneau factoriel est un cas particulier d anneau commutatif, unitaire et intègre. À l image des nombres entiers, il existe un équivalent du théorème fondamental de l arithmétique pour une telle structure. Tout élément d un… … Wikipédia en Français
Anneau Z/nZ — En mathématiques, et plus particulièrement en algèbre, Z/nZ est un cas particulier d anneau. Tout anneau unitaire contient soit un sous anneau isomorphe à Z/nZ soit à Z l anneau des entiers. Cet anneau joue un rôle particulier en arithmétique, il … Wikipédia en Français
Anneau Commutatif — Dans la théorie des anneaux, un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. Cela signifie que pour tous les éléments a et b de l’anneau, on a a*b=b*a, en notant * cette loi de multiplication. L’étude des… … Wikipédia en Français
Anneau Noethérien — Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une addition et d une… … Wikipédia en Français
Anneau abélien — Anneau commutatif Dans la théorie des anneaux, un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. Cela signifie que pour tous les éléments a et b de l’anneau, on a a*b=b*a, en notant * cette loi de… … Wikipédia en Français
Anneau noetherien — Anneau noethérien Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une… … Wikipédia en Français
Anneau principal — Les anneaux principaux forment un type d anneaux commutatifs important dans la théorie mathématique de la divisibilité. Ce sont des anneaux intègres auxquels on peut étendre deux théorèmes qui, au sens strict, concernent l anneau des entiers… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Anneau euclidien

Sommaire