- Corps De Rupture
-
Corps de rupture
En mathématiques et plus précisément en algèbre dans le cadre de la théorie de Galois un corps de rupture d'un polynôme à coefficients dans un corps K est une extension algébrique de K contenant au moins une racine du polynôme.
Les corps de ruptures ne sont pas en général ceux utilisés dans le contexte de la théorie de Galois, car ils ne possèdent pas les bonnes propriétés nécessaires pour appliquer le théorème fondamental de la théorie de Galois. En revanche ils sont une étape dans la construction des corps de décompositions, qui eux dans le cas où le critère de séparabilité est assuré permettent d'appliquer le théorème fondamental.
Sommaire
Motivation
Soit K un corps et P(X) un polynôme à coefficient dans K. une question naturelle se pose, existe-t-il une extension algébrique L du corps K contenant une ou plusieurs racines du polynôme? La réponse est positive, de plus il est possible de construire une extension finie ayant ces propriétés. Cette extension s'appelle un corps de rupture.
La technique utilisée consiste à quotienter l'anneau des polynômes par un idéal principal et plus précisément par un idéal maximal, c’est-à-dire un idéal contenu dans aucun autre idéal que l'anneau K[X]. Cette technique permet de construire un nouveau corps. Il est alors nécessaire d'identifier le corps K avec un sous-corps de L pour permettre au polynôme d'opérer sur L.
Soit (L, j) une extension de corps d'un corps K et P(X) un polynôme à coefficients dans K. Si l'on note K* l'image de K par j, alors il existe un isomorphisme φ naturel de K[X] dans K*[X] défini par:
![Soit \; (a_i) \in K^n \; tel \,que \; P(X)= \sum_{i \in [1,n]} a_i X^n \; alors \; \varphi(P)(X) = \sum_{i \in [1,n]} j(a_i) X^n](/pictures/frwiki/55/7fb6662ebf2eea8611db63baffe75090.png)
L'identification de K et K* permet d'identifier K[X] et K*[X] à travers l'isomorphisme d'anneau φ. P(X) apparaît alors comme un élément de L[X] à coefficients dans K inclus dans L. Un polynôme de K[X] opère donc naturellement sur L. Il est alors possible de parler de racine de P(X) dans L.
Si un corps de rupture possède le mérite d'exister, en revanche il ne contient pas, en général l'intégralité des racines de P(X). Il apparaît alors nécessaire de réitérer l'opération jusqu'à ce qu'une extension algébrique contenant toutes les racines soit construite. On parle alors de corps de décomposition.
Définitions
Soit K un corps et P(X) un polynôme formel à coefficients dans K. Un polynôme formel est construit à l'aide d'une indéterminée X, il se différentie d'une fonction polynôme, construit à l'aide de la variable x.
Une définition généralement admise est la suivante[1] :
-
- Si P(X) est un polynôme irréductible, un corps de rupture de P(X) est une extension L de K contenant au moins une racine.
On démontre que tout corps de rupture contient un sous-corps isomorphe au quotient de K par l'idéal engendré par P(X). Pour cette raison, le terme corps de rupture désigne alors tout sous-corps isomorphe à ce quotient. L'expression : le corps de rupture désigne toujours un corps de cette nature[2]. Deux exemples de corps de rupture construit à l'aide d'un quotient de cette nature sont donnés dans l'article Indéterminée.
Elle contient néanmoins une ambigüité. L'expression corps de rupture est aussi utilisée dans le cas où le polynôme P(X) n'est pas irréductible. Dans ce cas, l'unicité de l'extension minimale n'est plus garantie. Ainsi, dans Q[X] (ici Q désigne le corps des nombres rationnels), le polynôme X4 - X2 - 2 possède deux corps de rupture de dimension minimale : Q[i] et Q[√2].
Exemples
Soit dans le corps des nombres réels, le polynôme X2 + 1. Dans son corps de coefficients, le polynôme ne contient aucune racine. En effet, tout carré du corps des nombres réels est positif. Un corps de rupture naturel de ce polynôme est celui des nombres complexes. Voir construction des nombres complexes
Soit dans le corps des nombres rationnels le polynôme X3 - 2. L'extension de corps engendrée par r la racine cubique de deux. C'est une extension qui apparaît comme un espace vectoriel de dimension trois ayant comme base (1, r, r2). Cependant cette extension ne contient pas toutes les racines du polynôme en effet, il en existe deux ayant une composante complexe et qui ne sont pas élément du corps.
Propriétés
- Soit P(X) un polynôme irréductible de degré n sur K, alors il existe un corps de rupture L. Sa dimension est égale au degré du polynôme.
- Soit P(X) un polynôme sur K, alors il existe un corps de rupture L sur K.
Soit L le corps de rupture d'un polynôme irréductible P(X) de degré n, alors la première proposition nous assure qu'il existe un corps de rupture. Il existe aussi des sous-corps de la clôture algébrique Ω contenant une racine de P(X). La clôture algébrique d'un corps est un sur-corps de K tel que tous les polynômes à coefficients dans le sur-corps soit scindé, c’est-à-dire se décomposent en produit de polynômes du premier degré. Si α est une racine de P(X) dans Ω alors K[α] est aussi un sur-corps de K contenant une racine du polynôme. La proposition suivante établit le lien entre le corps de rupture et les sous-corps de la clôture algébrique isomorphe au corps de rupture.
- Il existe au plus n morphismes de L dans Ω. Si P(X) est un polynôme séparable, alors il existe exactement n morphismes.
Une polynôme est dit séparable s'il n'admet pas de racine multiple. C'est en souvent le cas pour un polynôme irréductible, c'est toujours vrai pour les corps des nombres rationnels des nombres réels ou pour les corps finis. La dernière propriété est démontrée dans l'article sur les extensions séparables.
Démonstrations-
- Soit P(X) un polynôme irréductible de degré n sur K, alors il existe un corps de rupture L. Sa dimension minimale est égale à n.
Considérons alors l'anneau L défini par K[X] / (P) le quotient de l'anneau des polynômes à coefficients dans K par l'idéal engendré par P(X). L'application de K dans L qui associe à tout élément de K son polynôme (c'est un polynôme constant) est bien un morphisme.
- Montrons que L est un espace vectoriel sur K de dimension égale au degré de P(X).
La famille (1, α, α2, αn-1) où α est défini comme la classe de X est en effet une base de L. Cette famille est libre, car toute combinaison linéaire non nulle possède un représentant de degré strictement plus petit que n. Ce représentant ne peut être un multiple de P(X) et donc la combinaison linéaire n'est pas nulle. Soit alors A(X) un représentant d'un élément de L, la division euclidienne par P(X) montre qu'il existe un autre représentant R(X) de la classe de A(X) engendré par la famille. La classe de P(X) apparaît comme une combinaison linéaire de la base, égale à R(α), et la famille est génératrice. C'est donc bien une base et [L:K] est égal au degré du polynôme P(X).
- Montrons que L est un corps.
Comme il est déjà établi que L est un anneau, il suffit de démontrer que chaque élément différent de 0 est inversible. Soit l un élément non nul de L et R(X) un représentant dans K[X] de degré strictement inférieur à n. les deux polynômes R(X) et P(X) sont premiers entre eux car le dernier polynôme est irréductible et le premier de degré strictement inférieur à celui de P(X). L'identité de Bezout nous assure alors de l'existence de deux polynômes A(X) et B(X) tel que:

L est donc un corps extension de K de dimension le degré du polynôme P(X) contenant une racine α.
-
- Il existe une extension finie L de K tel que le polynôme P(X) admet au moins une racine dans L.
Si le polynôme admet une racine, alors l'extension est le corps K lui même. Dans le cas contraire, le polynôme se décompose en produit de polynômes irréductibles.
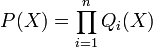
L'extension définie dans la proposition précédente contenant une racine de Q1(X) est finie, elle contient une racine du polynôme P(X), ce qui démontre la proposition.
Voir aussi
Référence
- ↑ Cette définition est par exemple celle donnée dans notion de théorie des corps de D. Harari ou encore celles de mathématiques.net
- ↑ Cette deuxième définition est enseignée en université, on la trouve par exemple dans un cours sur les corps finis de l'Université de Nice, dans une feuille d'exercice de l'Université Denis Diderot, c'est aussi la définition qu'en donne Espacemath
Liens externes
- (fr) Une courte présentation des extensions algébriques par Bernard le Stum Université de Rennes 1 2001
- (fr) Un cours de DEA sur la théorie de Galois par Alain Kraus Université de Paris VI 1998
- (fr) Corps des racines dans les-mathématiques.net
Références
- R. et A. Douady Algèbre et théories galoisiennes Cedic/Fernand Nathan 1978
- S. Lang Algebre Dunod 2004
- P. Samuel Théorie algébrique des nombres Hermann Paris 1971
- Portail des mathématiques
Catégorie : Théorie de Galois -
Wikimedia Foundation. 2010.
