Préordre

Préordre

Pré-ordre

Un pré-ordre (ou préordre[1]) est une relation binaire réflexive et transitive.

C'est-à-dire, si E est un ensemble, alors 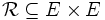{\mathcal R}\subseteq E\times E est un pré-ordre si et seulement si :

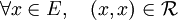  • \forall x \in E, \quad (x,x)\in{\mathcal R} (réflexivité)
  • \forall (x, y, z) \in E^3 \quad \left[(x,y)\in {\mathcal R} \and (y,z)\in {\mathcal R} \implies (x,z)\in{\mathcal R}\right] (transitivité)

Un pré-ordre antisymétrique est un ordre.

Un pré-ordre symétrique est une relation d'équivalence.

Exemples

  • Sur les sommets d'un graphe orienté, la relation « être accessible depuis » est un pré-ordre (c'est en fait la fermeture réflexive et transitive du graphe). Si le graphe est sans cycle, cette relation devient un ordre.
  • Dans un anneau commutatif, la relation «divise» est une relation de préordre.

Compléments

Si E et F sont des ensembles préordonnés par des relations de préordre qu'on notera toutes deux ≤, une application f de E dans F est dite[2] croissante si, pour toute paire d'éléments (x,y) de E tels que x ≤ y, on a aussi f(x) ≤ f(y).

Dans un ensemble E préordonné par une relation de préordre ≤, la relation « x ≤ y et y ≤ x » est une relation d'équivalence. Pour deux éléments X et Y de l'ensemble quotient, les deux conditions suivantes reviennent au même :

  • pour tout élément x de X et tout élément y de Y, x ≤ y;
  • il existe un élément x de X et un élément y de Y tels que x ≤ y.

Ces conditions équivalentes constituent une relation d'ordre dans l'ensemble quotient de E par la relation d'équivalence « x ≤ y et y ≤ x »[3].

Notes et références

  1. ↑ N. Bourbaki, Théorie des ensembles, ch. III, § 1, n° 2, (Paris, Masson, 1998, p. 2 et 5) écrit «préordre» et «préordonné».
  2. ↑ N. Bourbaki, Théorie des ensembles, ch. III, § 1, n° 5, (Paris, Masson, 1998, p. 7).
  3. ↑ N. Bourbaki, Théorie des ensembles, ch. III, § 1, n° 2, (Paris, Masson, 1998, p. 3).
Ce document provient de « Pr%C3%A9-ordre ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Préordre de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • préordre — ● préordre nom masculin Relation de préordre, relation binaire réflexive et transitive. ● préordre (expressions) nom masculin Relation de préordre, relation binaire réflexive et transitive. préordre [pʀeɔʀdʀ] n. m. ÉTYM. XXe; de pré , et ordre. ❖ …   Encyclopédie Universelle

  • Preordre de simulation — Préordre de simulation En informatique théorique un préordre de simulation est une relation entre systèmes de transition d états associant des systèmes qui se comportent de la même façon au sens qu un système simule l autre. Intuitivement, un… …   Wikipédia en Français

  • Préordre de simulation — En informatique théorique un préordre de simulation est une relation entre systèmes de transition d états associant des systèmes qui se comportent de la même façon au sens qu un système simule l autre. Intuitivement, un système simule l autre s… …   Wikipédia en Français

  • Relation de préordre — ● Relation de préordre relation binaire réflexive et transitive …   Encyclopédie Universelle

  • Pré-ordre de simulation — Préordre de simulation En informatique théorique un préordre de simulation est une relation entre systèmes de transition d états associant des systèmes qui se comportent de la même façon au sens qu un système simule l autre. Intuitivement, un… …   Wikipédia en Français

  • STATISTIQUE — Le mot «statistique» désigne à la fois un ensemble de données d’observation et l’activité qui consiste dans leur recueil, leur traitement et leur interprétation. Au cours de l’histoire, la collecte d’observations et la méthodologie de leur emploi …   Encyclopédie Universelle

  • Pre-ordre — Pré ordre Un pré ordre (ou préordre[1]) est une relation binaire réflexive et transitive. C est à dire, si E est un ensemble, alors est un pré ordre si et seulement si : (réflexivité) …   Wikipédia en Français

  • Pré-ordre — Un pré ordre (ou préordre[1]) est une relation binaire réflexive et transitive. C est à dire, si E est un ensemble, alors est un pré ordre si et seulement si : (réflexivité) …   Wikipédia en Français

  • Relation d'ordre — Une relation d’ordre dans un ensemble est une relation binaire dans cet ensemble qui permet de comparer ses éléments entre eux de manière cohérente. Un ensemble muni d’une relation d’ordre est un ensemble ordonné ou tout simplement un ordre.… …   Wikipédia en Français

  • Theorie de la decision — Théorie de la décision La théorie de la décision est une théorie de mathématiques appliquées ayant pour objet la prise de décision en univers risqué. Sommaire 1 Les limites de la théorie des probabilités 2 Risque ou incertitude ? 3 Gain non… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”