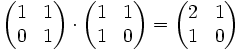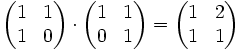Anneau abélien

Dans la théorie des anneaux, un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. Cela signifie que pour tous les éléments a et b de l’anneau, on a a*b=b*a, en notant * cette loi de multiplication.

L’étude des anneaux commutatifs s’appelle l’algèbre commutative.

Histoire

Voir la théorie des anneaux

Exemples

• L’exemple le plus important est l’anneau des entiers muni des lois d’addition et de multiplication ordinaires. La multiplication des entiers est commutative. L’anneau est souvent noté dans la littérature en référence au mot allemand « Zahlen » (nombres),
• Les nombres rationnels, les nombres réels et les nombres complexes forment des anneaux commutatifs, et même des corps commutatifs,
• plus généralement, tout corps commutatif est un anneau commutatif, et ainsi la classe des corps commutatifs est une sous classe de la classe des anneaux commutatifs,
• l’un des exemples les plus simples d’anneaux non commutatifs, est l’ensemble des matrices carrées d’ordre 2 à coefficients réels. Par exemple, le produit des matrices

n’est pas égal au produit de ces mêmes matrices dans l’ordre inverse

• si n est un entier strictement positif, alors l’ensemble Z/nZ des classes de congruence modulo n est un anneau commutatif à n éléments.
• si A est un anneau commutatif, alors les polynômes formels d’indéterminée X à coefficients dans A forment un nouvel anneau commutatif, noté A[X],
• de la même façon, l'ensemble des séries formelles, A[X₁,...,X_n] sur un anneau commutatif A est un anneau commutatif. Si A est un corps commutatif, alors l’anneau des séries formelles est un cas particulier d’anneau commutatif, appelé un anneau local,
• l’ensemble des nombres rationnels dont le dénominateur est impair forme un anneau commutatif, et en fait un anneau local. Cet anneau contient strictement l’anneau des entiers, et est lui-même un sous-ensemble propre du corps des rationnels,
• si p est un nombre premier, alors l’ensemble des entiers de l’ensemble des nombre p-adiques est un anneau commutatif.

Construction d’un nouvel anneau commutatif à partir d’un anneau commutatif donné

• Étant donné un anneau commutatif, A et un idéal I de A, l’anneau quotient A/I est l’ensemble des classes modulo I munie des lois définies par (a+I)+(b+I)=(a+b)+I et (a+I)(b+I)=ab+I.
• si A est un anneau commutatif donné, alors l’ensemble des polynômes A[X₁,...,X_n] à coefficients dans A forme un nouvel anneau commutatif, appelé l’anneau des polynômes en n indéterminées et à coefficients dans A ,
• si A est un anneau commutatif donné, alors l'ensemble des séries formelles A[[X₁,...,X_n]] à coefficients dans un anneau commutatif A, est appelé l’anneau des séries formelles de n indéterminées à coefficients dans A,
• si B est un sous-ensemble d’un anneau commutatif A, qui n’a aucun diviseur de zéro et qui est stable pour la multiplication, c’est-à-dire tel le produit de deux éléments quelconques de B appartienne à B, alors l’ensemble des fractions formelles (a, b) où a est un élément quelconque de A et b est un élément quelconque de B forme un nouvel anneau commutatif; l’addition, la soustraction, la multiplication et l’égalité étant définies sur ce nouvel ensemble de la même façon que pour les fractions ordinaires. Le nouvel anneau est noté A_B et est appelé la localisation de A à B.
  Un exemple illustrant ce qui précède est la localisation de l’anneau des nombres entiers au sous-ensemble des nombres entiers impairs stable par multiplication. Le corps des nombres rationnels est la localisation de l’anneau commutatif des nombres entiers à l’ensemble stable par multiplication de nombres entiers non nuls.
• si I est un idéal d’un anneau commutatif A, les puissances de I forment un voisinage topologique de 0 ce qui permet à A d’être considéré comme un anneau topologique. A peut être complété en conservant cette topologie. Par exemple, si est un corps, , l’anneau des séries formelles en une indéterminée à coefficients dans , est le complété de l’anneau des polynômes à coefficients dans , sous la topologie produite par les puissances de l'idéal engendré par X.

Remarques générales

La structure interne d'un anneau commutatif est déterminée par la considération de ses idéaux. Tous les idéaux dans un anneau commutatif sont des idéaux des deux côtés (à droite et à gauche), ce qui rend leur utilisation beaucoup plus aisée que dans le cas général.

La structure externe d'un anneau commutatif est déterminée par des considérations d'algèbre linéaire sur cet anneau, c'est-à-dire en étudiant les modules sur cet anneau. Cette étude est sensiblement plus difficile quand l’anneau commutatif n’est pas un corps commutatif et s’appelle habituellement l’algèbre homologique. L’ensemble des idéaux d’un anneau commutatif A peut être considéré comme l’ensemble des A-modules qui sont des sous-ensembles de A.

Les anneaux commutatifs sont parfois caractérisés par les éléments qu’ils contiennent qui ont des propriétés particulières. Un élément neutre pour la multiplication dans un anneau commutatif appelé élément unité, est un élément particulier (habituellement noté 1) tel que pour tout élément a de l’anneau, on ait 1 * a =a. Un anneau commutatif possédant un tel élément s’appelle un anneau unifère, ou parfois anneau unitaire.

Un élément a d’un anneau commutatif unifère est dit inversible s’il possède un symétrique pour la multiplication, c’est-à-dire s’il existe un élément de b de l’anneau (pas nécessairement distinct de a) tel que a*b = b*a = 1. Tout élément non nul d’un corps est un élément inversible. Tout élément d’un anneau local commutatif n’appartenant pas à l’idéal maximal est inversible.

Un élément différent de zéro a d’un anneau commutatif est dit diviseur de zéro, s’il existe un élément non nul b de l’anneau (pas nécessairement distinct de a) tel que a*b = 0. Un anneau commutatif unifère qui ne possède aucun diviseur de zéro est appelé un anneau intègre puisqu’il ressemble d’une certaine façon à celui des nombres entiers.

• Portail des mathématiques