- Icositétraèdre Pentagonal
-
Icositétraèdre pentagonal
Icositétraèdre pentagonal 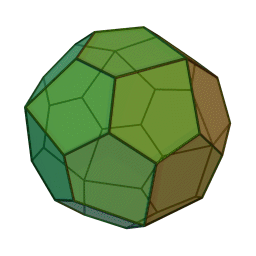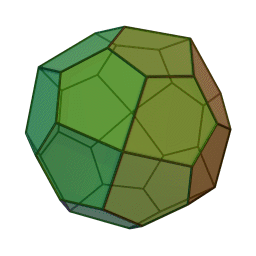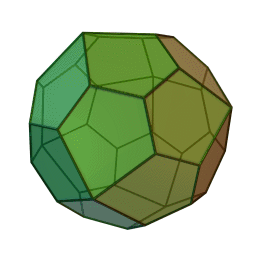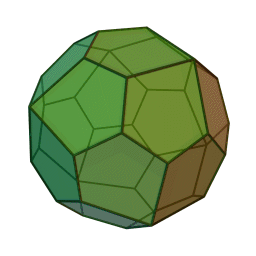
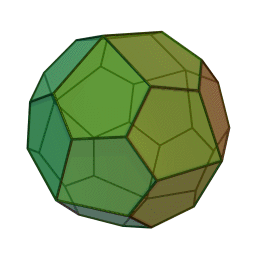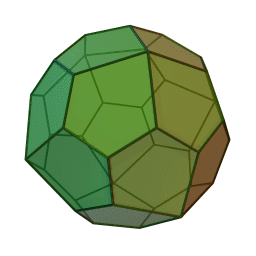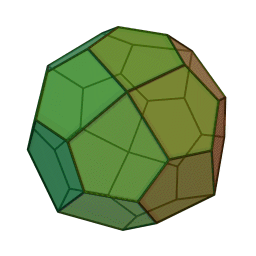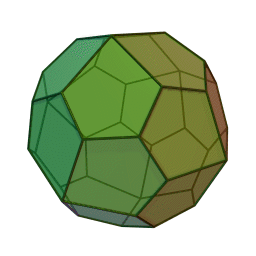
Type Solide de Catalan Faces Pentagones irréguliers Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
24
60
38
2Faces par sommet 3 et 4 Sommets par face 5 Isométries Octaédrique Dual Cube adouci Propriétés Convexe, uniformité des faces, chiral Un icosaèdre pentagonal est le polyèdre dual du cube adouci. C'est un solide de Catalan, c’est-à-dire un dual d'un solide d'Archimède. Il possède deux formes distinctes, qui sont les images l'une de l'autre dans un miroir (ou "énantiomorphes").
Références
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution - Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
