- Groupe Abélien Fini
-
Groupe abélien fini
 Leopold Kronecker (1823-1891)
Leopold Kronecker (1823-1891)
En mathématiques et plus précisément en algèbre, les groupes abéliens finis correspondent à une sous-catégorie de la catégorie des groupes.
Un groupe abélien fini est un groupe commutatif dont le cardinal est fini. Il correspond à un cas particulier des groupes abéliens de type fini. Ce concept dispose néanmoins d'une histoire propre et de nombreuses applications spécifiques, aussi bien théoriques comme en arithmétique modulaire qu'industrielles comme pour les code correcteurs.
Ces groupes vérifient une propriété forte : le théorème de Kronecker qui indique qu'ils sont tous des produits directs de groupes cycliques.
Sommaire
Histoire
En 1824, le mathématicien norvégien Niels Henrik Abel (1802 1829) publie, à ses propres frais un petit texte de six pages[1] étudiant la question de la résolution de l'équation générale du cinquième degré. Il met en évidence l'importance du caractère commutatif d'un ensemble de permutations. Un groupe commutatif porte maintenant le terme d'abélien en référence à cette découverte.
Évariste Galois (1811 1832) étudie la même question. En 1831, il utilise[2] pour la première fois le terme de groupe formel. Cet article est publié quinze ans plus tard par le mathématicien Joseph Liouville (1809 1882). Durant la deuxième moitié du XIXe siècle, l'étude des groupes finis apparait essentiel, initialement pour le développement de la théorie de Galois.
De nombreuses années sont néanmoins nécessaires pour définir cette notion de groupe formel. Kronecker est un acteur de cette axiomatisation. Il donne[3] en 1870 une définition équivalente à celle maintenant utilisée pour un groupe abélien fini. La définition générale est souvent attribuée à Heinrich Weber[4] (1842 1913).
En 1853 Leopold Kronecker (1823 1891) annonce que les extensions finies des nombres rationnels ayant un groupe de Galois abélien sont les sous-corps des extensions cyclotomiques[5]. Sa démonstration du théorème maintenant connu sous le nom de théorème de Kronecker-Weber est fausse, il faudra les apports de Richard Dedekind (1831 1916), Heinrich Weber[6] et enfin David Hilbert[7](1862 1943) pour une preuve rigoureuse. Ce contexte est celui qui amena Kronecker à démontrer le théorème fondamental des groupes abéliens finis qui porte maintenant son nom dans son article de 1870.
Propriétés
Propriétés élémentaires
-
- Tout groupe cyclique est un groupe abélien fini.
- Tout sous-groupe d'un groupe abélien fini est abélien et fini.
- Tout groupe quotient d'un groupe abélien fini est abélien fini.
- Tout produit direct d'une famille finie de groupes abéliens finis est un groupe abélien fini.
La première propriété est démontrée dans le paragraphe Théorème fondamental de l'article groupe cyclique, les autres sont le propre des groupes abéliens et des groupes finis.
Théorème de Kronecker
Article détaillé : Théorème de Kronecker.Dans le reste de l'article, G désigne un groupe abélien fini :
-
- Il existe une suite d'entiers strictement positifs (a1,a2,...,ak) tel que G est isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite.
Il existe donc la suite suivante isomorphe au groupe G:
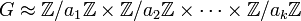
-
- Si la suite (a1,a2,...,ak) est choisie de tel sorte que ai+1 divise ai pour tout i entier entre 1 et k - 1, alors la suite est unique. Les éléments de cette suite sont appelés facteurs invariants.
Ce théorème est démontré dans l'article détaillé.
Conséquences du théorème de Kronecker
La définition suivante permet d'obtenir une autre décomposition :
-
- Soit p un nombre premier, un groupe abélien est dit de p-torsion si tous ses éléments sont d'ordre une puissance de p.
Dans le cas des groupes finis un groupe de p-torsion correspond exactement à la notion de p-groupe.
-
- Il existe une et une unique décomposition de G en produit de groupes de pi-torsions fini, à l'ordre près. Ici (pi) désigne une famille de nombres premiers.
Il existe aussi une autre décomposition plus fine :
-
- Il existe une unique décomposition de G en produit de cycles d'ordre une puissance d'un nombre premier.
On dispose de plus, de la propriété suivante :
-
- Soit d un diviseur de l'ordre de G, il existe un sous-groupe de G d'ordre d.
Démonstrations-
- Il existe une et une unique décomposition de G en produit de groupes de pi-torsions fini, à l'ordre près.
- Existence
Le théorème de Kronecker limite la démonstration au cas d'un groupe cyclique. En effet, comme tout groupe abélien fini est un produit de groupes cycliques, et que le produit direct d'un nombre fini de p-groupes est un p-groupe, il suffit alors de regrouper tous les p-groupes obtenus.
Le théorème chinois indique que si a et b sont deux entiers premiers entre eux alors Z/ab.Z est isomorphe à Z/a.Z x Z/b.Z. Il permet de conclure.
-
- Unicité
Il suffit pour cela de remarquer que le pi-groupe est formé des éléments dont l'ordre est une puissance de pi.
-
- Il existe une unique décomposition de G en produit de cycles d'ordre une puissance d'un nombre premier.
La proposition précédente limite la démonstration à l'existence et l'unicité d'une décomposition en produit direct de cycles pour un p-groupe.
- L'existence est une conséquence directe du théorème de Kronecker.
- L'unicité se démontre par récurrence.
- Si le p-groupe est de cardinal p, alors il n'admet pas de sous-groupe et sa décomposition est unique.
- Supposons la démonstration établie à l'ordre pk, montrons qu'elle est aussi vraie à l'ordre pk + 1. Soit pl l'exposant du p-groupe, toute décomposition en produit de cycle contient au moins un groupe cyclique d'ordre pl et ne contient aucun cycle d'ordre pm avec m > l (sinon l'exposant serait égal à pm). La démonstration du théorème de Kronecker montre qu'il existe une unique décomposition du p-groupe en un groupe cyclique d'ordre pl et d'un sous-groupe G'. L'hypothèse de récurrence montre l'unicité de la décomposition du groupe G' et termine la démonstration.
- Il existe un sous-groupe de G d'ordre d.
Soit g l'ordre du groupe G, le théorème de Kronecker indique qu'il existe un isomorphisme entre G et un produit de cycles :
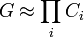
soit ci l'ordre de Ci, le produit des ci est égal à g, donc il existe une famille d'entiers di tel que di divise ci et que le produit des di soit égal à d. Il existe un sous-groupe Di de Ci d'ordre di (cf troisième proposition du paragraphe Théorème fondamental de l'article Groupe cyclique). Le produit des sous-groupes Di est isomorphe à un sous-groupe de G d'ordre d.
Applications
Analyse harmonique
Article détaillé : Analyse harmonique sur un groupe abélien fini.Un groupe abélien fini possède des caractères de groupe remarquables, les caractères du groupe sont isomorphes au groupe lui-même. La théorie de l'analyse harmonique est alors simple à établir. Il est ainsi possible de définir la transformation de Fourier ou le produit de convolution. Les résultats usuels comme l'égalité de Parseval, la théorème de Plancherel ou encore la formule sommatoire de Poisson sont vérifiés.
Arithmétique modulaire
Articles détaillés : Arithmétique modulaire et Symbole de Legendre.Une structure largement utilisé en théorie algébrique des nombres est celle de Z/pZ et particulièrement son groupe des unités. Cette approche est la base de l'arithmétique modulaire. Si p est un nombre premier, alors le groupe multiplicatif est cyclique d'ordre p - 1. Dans le cas contraire, le groupe des unités est encore abélien et fini.
Il aide à la résolution d'équations diophantiennes comme le petit théorème de Fermat, ainsi que la généralisation d'Euler. Il est aussi utilisé dans la démonstration du théorème des deux carrés de Fermat par Richard Dedekind.
L'analyse harmonique sur les groupes abéliens finis possèdent aussi de nombreuses applications en arithmétique. Elle correspondent à la formalisation moderne de résultats démontrés par des mathématiciens comme Carl Friedrich Gauss (1777 1855) ou Adrien-Marie Legendre (1752 1833). Le symbole de Legendre apparait maintenant comme un caractère d'un groupe cyclique, donc abélien et fini, à valeur dans {-1, 1}. Les sommes ou les périodes de Gauss s'exprime aussi à l'aide de caractères sur un groupe abélien fini, ce qui permet de les calculer. Cette approche est à la base d'une démonstration de la loi de réciprocité quadratique.
Johann Peter Gustav Lejeune Dirichlet (1805 - 1859) s'intéresse à une conjecture de Gauss et Legendre : toute classe du groupe des unités de l'anneau Z/nZ contient une infinité de nombres premiers. Leonhard Euler (1707 - 1783) propose bien une méthode, à travers le produit eulérien pour répondre, cependant les nombres premiers recherchés sont tous localisés dans une unique classe. Dirichlet utilise l'analyse harmonique pour démontrer ce théorème maintenant connu sous le nom de théorème de la progression arithmétique. Ses travaux sont fondateurs de la théorie analytique des nombres.
Théorie de Galois
Article détaillé : Théorème d'Abel-Ruffini.Les groupes abéliens finis ont un rôle particulier dans la théorie de Galois. Une conséquence du théorème d'Abel-Ruffini est que tout polynôme ayant un groupe de Galois abélien est résoluble par radicaux. La réciproque est un peu plus complexe, le groupe ne doit pas être nécessairement abélien mais résoluble. Le corps de décomposition d'un tel polynôme est une extension abélienne, c'est-à-dire une extension dont le groupe de Galois est abélien. Ce résultat rend donc les extensions abéliennes et leur groupe particulièrement intéressant. C'est la raison pour laquelle les mathématiciens du XIXe siècle ont cherché à démontrer le théorème de Kronecker-Weber avec tant d'assiduité.
Bien avant les découvertes de Galois Kronecker et Weber, Gauss avait utilisé un cas particulier : l'équation cyclotomique d'indice 17 pour trouver une méthode de construction à la règle et au compas de l'heptadécagone, c'est-à-dire du polygone régulier à 17 côtés. Le fait que le groupe de Galois du polynôme soit abélien est un élément essentiel de la méthode.
Corps fini
Article détaillé : Corps fini.Un corps fini Fd est construit sur deux structures de groupes différentes celle additive (Fd, + ) qui est un produit d'un même groupe cyclique d'ordre un nombre premier et (Fd*, . ) qui est un groupe cyclique.
Théorie de l'information
Article détaillé : Théorie de l'information.Au XXe siècle, les groupes abéliens finis prennent une importance particulière grâce à la naissance de la théorie de l'information. Ils sont utilisés à la fois pour la cryptologie et les codes correcteurs.
En cryptologie, les groupes cycliques à la base de nombreux algorithmes. L'arithmétique modulaire permet, par exemple, d'obtenir des tests de primalité comme celui de Fermat, ou de Miller-Rabin. L'utilisation des groupes abéliens finis ne s'arrête pas là. Une structure essentielle est celle d'un espace vectoriel de cardinal fini, donc sur un corps fini et de dimension fini. Elle correspond à un groupe abélien fini et permet de définir une analyse harmonique particulière. Si le corps contient deux éléments, les fonctions de l'espace vectoriel dans le corps des nombres complexes prend le nom de fonction booléenne et la transformée de Fourier celui de transformée de Walsh. La cryptologie utilise largement les fonctions booléennes et la transformée de Walsh, par exemple pour l'étude des boîtes-S.
La théorie des codes correcteurs et particulièrement celle des codes linéaires n'est pas en reste. Elle utilise, par exemple, l'analyse harmonique sur les espaces vectoriels finis quelconques pour l'analyse d'un code dual à travers l'identité de Mac Williams. Le code utilisé pour les disques compacts est de type Reed-Solomon, il utilise un espace vectoriel sur un corps à 256 éléments, une structure fondée sur de multiples groupes abéliens finis.
Notes et références
Notes
- ↑ Niels Henrik Abel Mémoire sur les équations algébriques, où l'on démontre l'impossibilité de la résolution de l'équation générale du cinquième degré 1824
- ↑ Evariste Galois sur les conditions de résolubilité des équations algébriques 1846 Journal de Liouville
- ↑ Leopold Kronecker Auseinandersetzung einiger Eigenschaften der Klassenzahl idealer complexer Zahlen Monatsber. K. Preuss. Akad. Wissenschaft. pp. 881–889 Berlin 1870
- ↑ Heinrich Weber Lehrbuch der Algebra Braunschweig 1896
- ↑ Leopold Kronecker Mémoire sur les facteurs irréductibles de l'expression xn - 1 Œuvres Tome 1 p 75 1854
- ↑ Heinrich Weber Theorie der Abel'schen Zahlkörper Acta Math T VIII et IX 1886 et 1887
- ↑ David Hilbert Ein neuer Beweis des Kronecker'schen Fundamentalsatzes über Abel'sche Zahlkörper Nachr. der K. Ges. der Wiss. zu Gottingen 1896
Liens externes
- (en) A history of Group theory par William Comb
- (fr) Un ensemble de mathématiciens de l'antiquité à aujourd'hui par J-M de Koninck et B R Hodgson
- (fr) Groupes abéliens cours d'algèbre de l'Université Claude Bernard Lyon I, par Fokko du Cloux
- (fr) Groupe abélien sur les mathématiques.net
Références
- S. Lang Algebre Dunod 2004
- J.F. Labarre La theorie des groupes Presses Universitaires de France (PUF) 1978
- Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
- Portail des mathématiques
Catégorie : Théorie des groupes -
Wikimedia Foundation. 2010.