- Groupe abelien
-
Groupe abélien
En algèbre générale, un groupe abélien, ou groupe commutatif, est un groupe
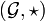dont la loi de composition interne 
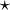est commutative, c’est-à-dire que pour tous les éléments 
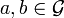, on a 
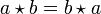.Les groupes abéliens portent le nom de Niels Henrik Abel.
Sommaire
Notations habituelles
Il y a deux notations courantes pour les groupes abéliens : la notation additive et la notation multiplicative.
Convention Opération Identité Puissance Inverse Somme directe/produit Addition x + y 0 nx −x G ⊕ H Multiplication x * y ou xy e ou 1 xn x −1 G × H La notation multiplicative est la notation habituelle pour les groupes, la notation additive étant préférée pour les modules. La notation additive est également courante lorsque les groupes abéliens sont étudiés à part des autres groupes.
Exemples
Des exemples de groupes abéliens incluent les groupes monogènes tels que l'ensemble des entiers
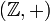et l'ensemble des entiers modulo n 
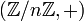.L'ensemble des nombres réels,
, forme un groupe abélien avec l'addition ; de même que l'ensemble des nombres réels non nuls,
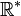, pour la multiplication. De la même façon tout corps 
renferme deux groupes,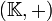 
muni de l'addition sur ce corps et 
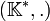privé de l'élément absorbant muni de la multiplication sur ce corps. Un autre exemple important est celui du groupe quotient 
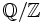.Si n est un entier naturel et x est un élément d'un groupe abélien
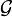, alors nx peut être défini comme x + x + ... + x (n sommes) et (-n)x = -(nx). De cette façon, 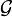devient un module sur l'anneau 
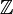des entiers. En fait, les modules sur 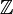peuvent être identifiés avec les groupes abéliens.Les théorèmes sur les groupes abéliens peuvent souvent être généralisés en théorèmes sur les modules sur un anneau principal.
Un exemple est la classification des groupes abéliens de type fini.
Propriétés
Tout sous-groupe d'un groupe abélien est un sous-groupe distingué, et ainsi les groupes quotients peuvent être formés librement.
Les sous-groupes, les groupes quotients, les produits et les sommes directes de groupes abéliens, sont aussi abéliens.
Si f, g : G → H sont deux homomorphismes entre groupes abéliens, alors leur somme f+g, définie par (f+g)(x) = f(x) + g(x), est aussi un homomorphisme. (ce qui n'est pas vrai si H n'est pas un groupe abélien). L'ensemble Hom(G, H) de tous les homomorphismes de groupes de G vers H devient ainsi lui-même un groupe abélien.
Les groupes abéliens, conjointement avec les homomorphismes, forment une catégorie, prototype d'une catégorie abélienne.
Rang
Quelque peu apparenté à la dimension d'un espace vectoriel, tout groupe abélien a un rang. Le rang est défini comme le cardinal du plus grand ensemble d'éléments linéairement indépendants du groupe. Les ensembles des nombres entiers et des nombres rationnels respectivement ont un rang égal à un. Alors que les rangs des groupes abéliens finis sont bien compris, les rangs des groupes infinis peuvent être extrêmement complexes et encore beaucoup de questions en suspens subsistent, souvent intimement liées à des questions de la théorie des ensembles.
Topologie
Beaucoup de grands groupes abéliens portent une topologie naturelle, les transformant en des groupes topologiques.
Portail des mathématiques
Catégorie : Groupe
Wikimedia Foundation. 2010.
