- Theoreme de Kronecker
-
Théorème de Kronecker
En mathématiques et plus particulièrement en algèbre, le théorème de Kronecker traite des groupes abéliens finis.
Le théorème de Kronecker est aussi appelé théorème fondamental des groupes abéliens finis. Il stipule que tout groupe abélien fini est isomorphe à un produit direct de groupes cycliques.
Ce théorème doit son nom à Leopold Kronecker (1823-1891) qui l'a démontré la première fois en 1870 dans un article intitulé Auseinandersetzung einiger Eigenschaften der Klassenzahl idealer complexer Zahlen Monatsber.
Sommaire
Enoncé du théorème
Soit G un groupe abélien fini.
-
- Il existe une unique suite (a1,a2,...,ak) d'entiers > 1 telle que G soit isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite:
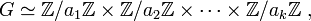
-
- et que ai+1 divise ai pour tout i entier entre 1 et k - 1.
- Les éléments de cette suite sont appelés facteurs invariants de G.
Démonstration
Il existe de nombreuses manières de démontrer ce théorème. Une des méthodes les plus expéditives utilise la théorie des représentation des groupes. La démonstration se trouve au paragraphe représentation de groupe fini commutatif. Il en existe d'autres utilisant par exemple les caractères. La démonstration proposée ici reste dans le cadre strict de la théorie des groupes. Elle se fonde sur une décomposition en somme directe.
La démonstration se fonde sur la construction d'un projecteur φ dont l'image est le groupe cyclique C1 d'ordre θ l'exposant du groupe. Les projecteurs d'un groupe abélien sont étudiés dans le paragraphe Projecteur de l'article Produit direct (groupes).
Soit B une famille génératrice (g1,g2,...,gk) tel que l'ordre de g1 soit égal à θ. Une telle famille existe toujours car le groupe est fini. Il est toujours possible d'adjoindre à cette famille un élément g1 d'ordre θ.
La technique consiste à définir le morphisme sur C1 comme étant égal à l'identité, puis de prolonger ce morphisme sur le groupe engendré par g1 et g2 puis sur le groupe engendré par g1, g2 et g3 jusqu'à gk. La démonstration procède donc par récurrence sur k.
DétailsExistence de la décomposition
- I) Pour tout groupe abélien fini généré par une famille B ne contenant qu'un seul élément, il est possible de construire le projecteur φ.
Il suffit de définir φ comme égal à l'identité. φ est un projecteur dont le noyau est réduit à l'élément neutre.
- II) Supposons qu'il soit possible de construire un projecteur φ sur le groupe cyclique C1 pour tout groupe ayant une famille B de cardinal p - 1. Alors ce résultat est aussi vrai pour tout groupe G ayant une famille B de cardinal p.
Notons (g1,g2,...,gp) la famille B de G. Alors si G' est le groupe engendré par les éléments (g1,g2,...,gp - 1), il vérifie l'hypothèse de récurrence. Il existe donc un projecteur φ' défini sur G' dont l'image est égale à C1.
-
- II) 1) Construction de φ:
Notons m l'ordre de gp. L'intersection H du sous-groupe <gp> et de G' est un groupe cyclique car c'est un sous-groupe du groupe cyclique <gp>. Soit u son ordre, u divise m d'après le théorème de Lagrange. Notons v l'entier défini par u.v = m. L'élément v.gp est un générateur de H (cf troisième propriété du paragraphe Théorème fondamental des groupes cycliques).
L'élément v.gp est un membre de H, or l'application φ' est définie sur H, il existe donc un entier t tel que:
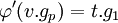
v.u.gp est égal à 0 car u.v est l'ordre de gp. Donc u.t.g1 est aussi égal à 0 ce qui montre que u.t est un multiple de θ. Il existe donc un entier w tel que:
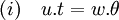
u.v est l'ordre de gp, un élément du groupe G. L'ordre de tout élément de G divise θ par définition de l'exposant d'un groupe. En conclusion il existe un entier x tel que x.u.v soit égal à θ. En remplaçant θ par sa valeur dans l'égalité (i) on obtient:

On définit alors φ par l'égalité suivante:
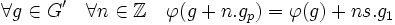
-
- II) 2) L'application φ est bien le projecteur recherché :
Si G est bien la somme de G' et <gp>, en revanche cette somme n'est pas nécessairement directe. Il existe donc plusieurs écritures potentielles d'un élément de G. Il convient de vérifier que toute écriture d'un même élément de G possède la même image par φ.
Soit g + n .gp et g' + n' .gp deux écritures d'un même élément du groupe G. Alors g - g' est à la fois un élément de G' et de <gp> car il est égal à (n' -n). gp. Cela démontre l'existence d'un entier l tel que g = g' + l.v.gp et l.v = n' - n.
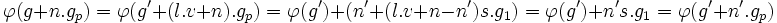
φ est un endomorphisme de G, en effet :
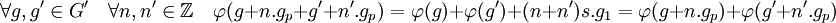
Enfin, par construction de φ, l'image de φ est égal à C1 et la restriction de φ à son image est l'identité. L'application φ est un projecteur d'image C1. en conclusion G est somme directe de C1 et du noyau de φ.
- III) Démonstration du théorème par récurrence sur le cardinal de G.
Si G est d'ordre 1. Le théorème est évident.
Supposons le théorème démontré pour tous les groupes abéliens finis d'ordre strictement inférieur à n. Soit G un groupe abélien fini d'ordre n. Alors il existe un projecteur sur un groupe cyclique d'ordre l'exposant de G. G est donc somme directe du groupe cyclique et du noyau K du projecteur.
L'hypothèse de récurrence montre que K est somme directe d'une suite de sous-groupes cycliques C2,...,Ck tel que si i est un entier compris entre 2 et k - 1, alors l'ordre de Ci+1 divise l'ordre de Ci. De plus l'ordre de C2 divise l'ordre de C1 qui est égal à l'ordre de l'exposant de G, car l'ordre de tout élément de G divise l'exposant de G.
L'analyse de la somme directe de la suite de sous-groupes C1, C2,...,Ck démontre alors le théorème.
Unicité de la décomposition :
-
- Si la suite (a1,a2,...,ak) est choisie de tel sorte que ai+1 divise ai pour tout i est un entier entre 1 et k - 1, alors la suite est unique.
L'existence est donnée par la démonstration précédente. Prouvons l'unicité par une récurrence sur k.
- I) Si k est égal à 1:
Le groupe est cyclique et a1 est égal à l'ordre du groupe, ce qui démontre la proposition.
- II) Si la propriété est vraie à l'ordre p - 1, alors elle est vraie à l'ordre p.
Soit G un groupe décomposable en un produit de p cycles et une suite (a1,a2,...,ap), vérifiant les propriétés de l'hypothèse. Alors a1 est égal à l'exposant du groupe, il est donc unique. Soit Ci le groupe cyclique d'ordre ai. Le produit K des p - 1 derniers groupes Ci est isomorphe au quotient G / C1 et est donc aussi unique. Par hypothèse de récurrence, K admet une suite unique de facteurs invariants, les valeurs (a2,a3,...,ap) sont donc uniques. Il suffit alors de vérifier que a2 divise a1. Pour cela remarquons que a2 est l'exposant d'un sous-groupe de G et donc divise l'exposant du groupe. Et la proposition est démontrée.
Généralisations
- Le théorème de Jordan-Hölder est un théorème analogue dans le cas où le groupe n'est pas abélien.
- Un théorème structurel existe aussi dans le cas où le groupe n'est plus fini mais de type fini.
Références
Liens externes
- (fr) Groupes abéliens cours d'algèbre de l'Université Claude Bernard Lyon I, par Fokko du Cloux
- (fr) Groupe abélien sur les mathématiques.net
- (fr) Structure des groupes abéliens finis (une approche par les caractères) Colas Bardavid
Références
- S. Lang Algebre Dunod 2004
- J.F. Labarre La theorie des groupes Presses Universitaires de France (PUF) 1978
- Portail des mathématiques
Catégories : Théorie des groupes | Théorème d'algèbre -
Wikimedia Foundation. 2010.

