Exposant D'un Groupe

Exposant d'un groupe

L'exposant d'un groupe est une notion mathématiques et plus précisément d'algèbre, en théorie des groupes.

Elle est utilisée surtout pour les groupe abélien finis, par exemple pour la démonstration du théorème de Kronecker. Elle correspond à une hypothèse du problème de Burnside, on la trouve donc dans le théorème de Burnside associé.

Sommaire

1 Définition
2 Propriétés
3 Références
- 3.1 Liens externes
- 3.2 Références

Définition

Soit G un groupe, on appelle exposant de G le plus petit commun multiple des ordres des éléments du groupe s'il existe.

L'ordre d'un élément g du groupe désigne, s'il existe, le plus petit entier strictement positif n vérifiant gⁿ = 1 où 1 désigne l'unité du groupe.

Dans le cas d'un groupe contenant un élément d'un ordre infini ou si le plus petit commun multiple n'existe pas, ce qui ne se produit que dans le cas d'un groupe d'ordre infini, on dit que l'exposant n'est pas fini.

Propriétés

L'exposant d'un groupe fini est nécessairement inférieur ou égal à l'ordre du groupe. En effet, l'ordre du groupe est un multiple de chacun des ordres des éléments du groupe d'après le théorème de Lagrange. Dans le cas où le groupe est en plus abélien, une propriété plus forte existe:

Tout groupe abélien fini contient au moins un élément dont l'ordre est égal à l'exposant.

Démonstration

Soit $θ$ l'exposant d'un groupe fini abélien G. Considérons alors la décomposition du théorème fondamental de l'arithmétique de l'exposant:

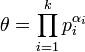
$\theta = \prod_{i=1}^k p_i^{\alpha_i}$

Où p_i désigne des nombres premiers et $α$ _i des entiers strictement positifs.

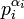Il existe au moins un élément a_i d'ordre $p_i^{\alpha_i}$ .

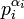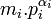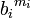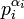Il existe au moins un élément b_i ayant un ordre multiple de $p_i^{\alpha_i}$ sinon ce facteur ne serait pas membre de la décomposition de θ en facteurs premiers. Il existe donc un entier m_i tel que $m_i.p_i^{\alpha_i}$ soit l'ordre de b_i. Si a_i est égal à ${b_i}^{m_i}$ , alors a_i est d'ordre $p_i^{\alpha_i}$ .

Il existe un moins un élément g d'ordre l'exposant du groupe.

Tous les ordres des éléments a_i sont premiers entre eux par construction. Le théorème chinois montre alors que le produit g des a_i a pour ordre le produit des ordres des a_i. On en conclut que l'ordre de g est l'exposant du groupe.

Références

Liens externes

(fr) Exposant d'un groupe abélien par Bibmath.net
(fr) Groupe abélien sur les mathématiques.net
(fr) Structure des groupes abéliens finis (une approche par les caractères) Colas Bardavid

Références

S. Lang Algebre Dunod 2004

J.F. Labarre La theorie des groupes Presses Universitaires de France (PUF) 1978

Portail des mathématiques

Ce document provient de « Exposant d%27un groupe ».

Catégorie : Théorie des groupes

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Exposant D'un Groupe de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Exposant d'un groupe — En algèbre générale, l exposant d un groupe est une notion de théorie des groupes. On peut l utiliser pour démontrer le théorème de Kronecker sur la structure des groupes abéliens finis. Elle correspond à une hypothèse du problème de Burnside de… … Wikipédia en Français
Exposant (Mathématiques) — Pour les articles homonymes, voir Exposant. En mathématiques, il est souvent intéressant de multiplier un nombre a par lui même plusieurs fois de suite. Dans une telle opération, l exposant est le nombre de facteurs intervenant dans cette… … Wikipédia en Français
Exposant (mathematiques) — Exposant (mathématiques) Pour les articles homonymes, voir Exposant. En mathématiques, il est souvent intéressant de multiplier un nombre a par lui même plusieurs fois de suite. Dans une telle opération, l exposant est le nombre de facteurs… … Wikipédia en Français
Groupe Abélien Fini — Leopold Kronecker (1823 1891) En mathématiques et plus précisément en algèbre, les groupes abéliens finis correspondent à une sous catégorie de la catégorie des groupes. Un groupe abélien fini est un groupe commutatif dont le cardinal est fini.… … Wikipédia en Français
Groupe abelien fini — Groupe abélien fini Leopold Kronecker (1823 1891) En mathématiques et plus précisément en algèbre, les groupes abéliens finis correspondent à une sous catégorie de la catégorie des groupes. Un groupe abélien fini est un groupe commutatif dont le… … Wikipédia en Français
Groupe abélien fini — Leopold Kronecker (1823 1891) En mathématiques et plus précisément en algèbre, les groupes abéliens finis correspondent à une sous catégorie de la catégorie des groupes. Un groupe abélien fini est un groupe commutatif dont l ensemble sous jacent… … Wikipédia en Français
Exposant — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Exposant », sur le Wiktionnaire (dictionnaire universel) Exposant peut signifier: L exposant, une… … Wikipédia en Français
exposant — exposant, ante [ ɛkspozɑ̃, ɑ̃t ] n. • 1389 dr. « demandeur »; subst. particip. de exposer 1 ♦ (1820) Personne dont les œuvres, les produits sont présentés dans une exposition (2o). Le stand d un exposant, dans une foire. « Je regrette de ne pas… … Encyclopédie Universelle
Groupe Abélien De Type Fini — Les groupes abéliens de type fini forment une sous catégorie particulière d objets mathématiques de la catégorie des groupes abstraits. Ce sont les groupes qui sont, d une part, abéliens, c’est à dire ceux dont la loi de composition interne est… … Wikipédia en Français
Groupe abelien de type fini — Groupe abélien de type fini Les groupes abéliens de type fini forment une sous catégorie particulière d objets mathématiques de la catégorie des groupes abstraits. Ce sont les groupes qui sont, d une part, abéliens, c’est à dire ceux dont la loi… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Exposant D'un Groupe