Theorie de l'information

Theorie de l'information: Théorie de l'information

La théorie de l'information, sans précision, est le nom usuel désignant la théorie de l'information de Shannon, qui est une théorie probabiliste permettant de quantifier le contenu moyen en information d'un ensemble de messages, dont le codage informatique satisfait une distribution statistique précise. Ce domaine trouve son origine scientifique avec Claude Shannon qui en est le père fondateur avec son article A Mathematical Theory of Communications publié en 1949.

L'apparition de la théorie de l'information est liée à l'apparition de la psychologie cognitive^{[réf. souhaitée]} dans les années 1940 - 1950.

Parmi les branches importantes de la théorie de l'information de Shannon, on peut citer :

le codage de l'information,

la mesure quantitative de redondance d'un texte,

la compression de données,

la cryptographie.

Dans un sens plus général, une théorie de l'information est une théorie visant à quantifier et qualifier la notion de contenu en information présent dans un ensemble de données. A ce titre, il existe une autre théorie de l'information : la théorie algorithmique de l'information, initialisée par Kolmogorov, Solomonov et Chaitin au début des années 1960.

Sommaire

1 Historique

2 Exemples d'information

2.1 Premier exemple

2.2 Second exemple

2.3 Information imparfaite

3 Contenu d'information et contexte

4 Mesure de la quantité d'information

4.1 Quantité d'information : cas élémentaire

4.2 Quantité d'information relative à un évènement

4.3 Entropie, formule de Shannon

4.4 Codage de l'information

5 Voir aussi

6 Bibliographie

7 Liens externes

Historique

La théorie de l'Information résulte initialement des travaux de Ronald Aylmer Fisher. Celui-ci, statisticien, définit formellement l'information comme égale à la valeur moyenne du carré de la dérivée du logarithme de la loi de probabilité étudiée.

$\mathcal{I}(\theta) = \mathrm{E} \left\{\left. \left[ \frac{\partial}{\partial\theta} \ln f(X;\theta) \right]^2 \right|\theta\right\}$

À partir de l'inégalité de Cramer, on déduit que la valeur d'une telle information est proportionnelle à la faible variabilité des conclusions résultantes. En termes simples, moins une observation est probable, plus son observation est porteuse d'information. Par exemple, lorsque le journaliste commence le journal télévisé par la phrase "Bonsoir", ce mot, qui présente une forte probabilité, n'apporte que peu d'information. En revanche, si la première phrase est, par exemple "La France a peur", sa faible probabilité fera que l'auditeur apprendra qu'il s'est passé quelque chose, et, partant, sera plus à l'écoute.

D'autres modèles mathématiques ont complété et étendu de façon formelle la définition de l'information.

Claude Shannon et Warren Weaver renforcent le paradigme. Ils sont ingénieurs en télécommunication et se préoccupent de mesurer l'information pour en déduire les fondamentaux de la Communication (et non une théorie de l'information). Dans Théorie Mathématique de la Communication en 1948, ils modélisent l'information pour étudier les lois correspondantes : bruit, entropie et chaos, par analogie générale aux lois d'énergétique et de thermodynamique. Leurs travaux complétant ceux d'Alan Turing, de Norbert Wiener et de John von Neumann (pour ne citer que les principaux) constituent le socle initial de la théorie du signal et des « Sciences de l'Information ».

Pour une source $X$ comportant $n$ symboles, un symbole $i$ ayant une probabilité $p i$ d'apparaître, l'entropie $H$ de la source $X$ est définie comme :

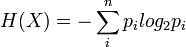
$H(X)=-\sum_i^n p_i log_2 p_i$

C'est au départ le logarithme népérien qui est utilisé. On le remplacera pour commodité par le logarithme à base 2, correspondant à une information qui est le bit. Les considérations d'entropie maximale (MAXENT) permettront à l'inférence bayésienne de définir de façon rationnelle ses distributions a priori.

L'informatique constituera une déclinaison technique automatisant les traitements (dont la transmission et le transport) d'information. L'appellation « Technologies de l'Information et de la Communication » recouvre les différents aspects (systèmes de traitements, réseaux, etc.) de l'informatique au sens large.

Les sciences de l'information dégagent du sens depuis des données en s'appuyant sur des questions de corrélation, d'entropie et d'apprentissage (voir Data mining). Les technologies de l'information, quant à elles, s'occupent de la façon de concevoir, implémenter et déployer des solutions pour répondre à des besoins identifiés.

Adrian Mc Donough dans Information economics définit l'information comme la rencontre d'une donnée (data) et d'un problème. La connaissance (knowledge) est une information potentielle. Le rendement informationnel d'un système de traitement de l'information est le quotient entre le nombre de bits du réservoir de données et celui de l'information extraite. Les data sont le cost side du système, l'information, le value side. Il en résulte que lorsqu'un informaticien calcule la productivité de son système par le rapport entre la quantité de données produites et le coût financier, il commet une erreur, car les deux termes de l'équation négligent la quantité d'information réellement produite. Cette remarque prend tout son sens à la lumière du grand principe de Russel Ackoff qui postule qu'au-delà d'une certaine masse de données, la quantité d'information baisse et qu'à la limite elle devient nulle. Ceci correspond à l'adage "trop d'information détruit l'information". Ce constat est aggravé lorsque le récepteur du système est un processeur humain, et pis encore, le conscient d'un agent humain. En effet, l'information est tributaire de la sélection opérée par l'attention, et par l'intervention de données affectives, émotionnelles, et structurelles absentes de l'ordinateur. L'information se transforme alors en sens, puis en motivation. Une information qui ne produit aucun sens est nulle et non avenue pour le récepteur humain, même si elle est acceptable pour un robot. Une information chargée de sens mais non irriguée par une énergie psychologique (drive, cathexis, libido, ep, etc.) est morte. On constate donc que dans la chaîne qui mène de la donnée à l'action (données -> information -> connaissance -> sens -> motivation), seule les deux premières transformations sont prises en compte par la théorie de l'information classique et par la sémiologie. Kevin Bronstein remarque que l'automate ne définit l'information que par deux valeurs : le nombre de bits, la structure et l'organisation des sèmes, alors que le psychisme fait intervenir des facteurs dynamiques tels que passion, motivation, désir, répulsion etc. qui donnent vie à l'information psychologique.

Exemples d'information

Une information désigne, parmi un ensemble d'événements, un ou plusieurs événements possibles.

En théorie, l'information diminue l'incertitude. En théorie de la décision, on considère même qu'il ne faut appeler information que ce qui est susceptible d'avoir un effet sur nos décisions (peu de choses dans un journal sont à ce compte des informations...).

En pratique, l'excès d'information, tel qu'il se présente dans les systèmes de messagerie électronique, peut aboutir à une saturation, et empêcher la prise de décision.

Premier exemple

Soit une source pouvant produire des tensions entières de 1 à 10 volts et un récepteur qui va mesurer cette tension. Avant l'envoi du courant électrique par la source, le récepteur n'a aucune idée de la tension qui sera délivrée par la source. En revanche, une fois le courant émis et réceptionné, l'incertitude sur le courant émis diminue. La théorie de l'information considère que le récepteur possède une incertitude de 10 états.

Second exemple

Une bibliothèque possède un grand nombre d'ouvrages, des revues, des livres et des dictionnaires. Nous cherchons un cours complet sur la théorie de l'information. Tout d'abord, il est logique que nous ne trouverons pas ce dossier dans des ouvrages d'arts ou de littérature; nous venons donc d'obtenir une information qui diminuera notre temps de recherche. Nous avions précisé que nous voulions aussi un cours complet, nous ne le trouverons donc ni dans une revue, ni dans un dictionnaire. nous avons obtenu une information supplémentaire (nous cherchons un livre), qui réduira encore le temps de notre recherche.

Information imparfaite

Soit un réalisateur dont j'aime deux films sur trois. Un critique que je connais bien éreinte son dernier film et je sais que je partage en moyenne les analyses de ce critique quatre fois sur cinq. Cette critique me dissuadera-t-elle d'aller voir le film ? C'est là la question centrale de l'inférence bayésienne, qui se quantifie aussi en bits.

Contenu d'information et contexte

Il faut moins de bits pour écrire chien que mammifère. Pourtant l'indication Médor est un chien contient bien plus d'information que l'indication Médor est un mammifère : le contenu d'information sémantique d'un message dépend du contexte. En fait, c'est le couple message + contexte qui constitue le véritable porteur d'information, et jamais le message seul (voir paradoxe du compresseur).

Mesure de la quantité d'information

Quantité d'information : cas élémentaire

Considérons $N$ boîtes numérotées de 1 à $N$ . Un individu A a caché au hasard un objet dans une de ces boîtes. Un individu B doit trouver le numéro de la boîte où est caché l'objet. Pour cela, il a le droit de poser des questions à l'individu A auxquelles celui-ci doit répondre sans mentir par OUI ou NON. Mais chaque question posée représente un coût à payer par l'individu B (par exemple un euro). Un individu C sait dans quelle boîte est caché l'objet. Il a la possibilité de vendre cette information à l'individu B. B n'acceptera ce marché que si le prix de C est inférieur ou égal au coût moyen que B devrait dépenser pour trouver la boîte en posant des questions à A. L'information détenue par C a donc un certain prix. Ce prix représente la quantité d'information représentée par la connaissance de la bonne boîte : c'est le nombre moyen de questions à poser pour identifier cette boîte. Nous la noterons I.

EXEMPLE :

Si $N = 1$ , $I = 0$ . Il n'y a qu'une seule boîte. Aucune question n'est nécessaire.

Si $N = 2$ , $I = 1$ . On demande si la bonne boîte est la boîte n°1. La réponse OUI ou NON détermine alors sans ambiguïté quelle est la boîte cherchée.

Si $N = 4$ , $I = 2$ . On demande si la boîte porte le n°1 ou 2. La réponse permet alors d'éliminer deux des boîtes et il suffit d'une dernière question pour trouver quelle est la bonne boîte parmi les deux restantes.

Si $N = 2 k$ , $I = k$ . On écrit les numéros des boîtes en base 2. Les numéros ont au plus $k$ chiffres binaires, et pour chacun des rangs de ces chiffres, on demande si la boîte cherchée possède le chiffre 0 ou le chiffre 1. En $k$ questions, on a déterminé tous les chiffres binaires de la bonne boîte. Cela revient également à poser $k$ questions, chaque question ayant pour but de diviser successivement le nombre de boîtes considérées par 2 (méthode de dichotomie).

On est donc amené à poser $I = l o g 2 (N)$ , mais cette configuration ne se produit que dans le cas de $N$ événements équiprobables.

Quantité d'information relative à un évènement

Supposons maintenant que les boîtes soient colorées, et qu'il y ait $n$ boîtes rouges. Supposons également que C sache que la boîte où est caché l'objet est rouge. Quel est le prix de cette information? Sans cette information, le prix à payer est $l o g (N)$ . Muni de cette information, le prix à payer n'est plus que $l o g (n)$ . Le prix de l'information « la boîte cherchée est rouge » est donc $l o g (N) - l o g (n) = l o g (N / n)$ .

On définit ainsi la quantité d'information comme une fonction croissante de 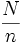$\frac{N}{n}$ avec :

$N$ le nombre d'évènements possibles

$n$ le cardinal du sous-ensemble délimité par l'information

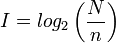
Afin de mesurer cette quantité d'information, on pose : $I = log_{2} \left (\frac{N}{n} \right)$

$I$ est exprimé en bit (ou logon, unité introduite par Shannon, de laquelle, dans les faits, bit est devenu un synonyme), ou bien en nat si on utilise le logarithme naturel à la place du logarithme de base 2.

Cette définition se justifie, car l'on veut les propriétés suivantes :

l'information est comprise entre 0 et ∞ ;

un évènement avec peu de probabilité représente beaucoup d'information (exemple : « Il neige en janvier » contient beaucoup moins d'information que « Il neige en août » pour peu que l'on soit dans l'hémisphère nord) ;

l'information doit être additive.

Remarque : lorsqu'on dispose de plusieurs informations, la quantité d'information globale n'est pas la somme des quantités d'information. Ceci est dû à la présence du logarithme. Voir aussi : information mutuelle, information commune à deux messages, qui, dans l'idée, explique cette « sous-additivité » de l'information.

Entropie, formule de Shannon

Supposons maintenant que les boîtes soient de diverses couleurs : n₁ boîtes de couleur C₁, n₂ boîtes de couleur C₂, ..., n_k boîtes de couleurs C_k, avec n₁ + n₂ + ... + n_k = N. La personne C sait de quelle couleur est la boîte recherchée. Quel est le prix de cette information ?

L'information « la boîte est de couleur C₁ » vaut log N/n₁, et cette éventualité a une probabilité n₁/N. L'information « la boîte est de couleur C2 » vaut log N/n₂, et cette éventualité a une probabilité n₂/N...

Le prix moyen de l'information est donc n₁/N log N/n₁ + n₂/N log N/n₂ + ... + n_k/N log N/n_k. Plus généralement, si on considère k évènements disjoints de probabilités respectives p₁, p₂, ..., p_k avec p₁ + p₂ + ... + p_k = 1, alors la quantité d'information correspondant à cette distribution de probabilité est p₁ log 1/p₁ + ... + p_k log 1/p_k. Cette quantité s'appelle entropie de la distribution de probabilité.

L'entropie permet donc de mesurer la quantité d'information moyenne d'un ensemble d'évènements (en particulier de messages) et de mesurer son incertitude. On la note $H$ :
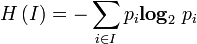
$H \left (I \right) = - \sum_{i\in I} p_i \mathbf{log}_2\; p_i$
avec 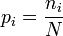$p_i = \frac{n_i}{N}$ la probabilité associée à l'apparition de l'évènement $i$ .

Voir l'article détaillé : entropie de Shannon.

Voir aussi une notion connexe : complexité de Kolmogorov.

Codage de l'information

On considère une suite de symboles. Chaque symbole peut prendre deux valeurs s₁ et s₂ avec des probabilités respectivement p₁ = 0,8 et p₂ = 0,2. La quantité d'information contenue dans un symbole est p₁ log 1/p₁ + p₂ log 1/p₂ ≈ 0,7219. Si chaque symbole est indépendant du suivant, alors un message de N symboles contient en moyenne une quantité d'information égale à 0,72N. Si le symbole s₁ est codé 0 et le symbole s₂ est codé 1, alors le message a une longueur de N, ce qui est une perte par rapport à la quantité d'information qu'il porte. Les théorèmes de Shannon énoncent qu'il est impossible de trouver un code dont la longueur moyenne soit inférieure à 0,72N, mais qu'il est possible de coder le message de façon à ce que le message codé ait en moyenne une longueur aussi proche que l'on veut de 0,72N lorsque N augmente.

Par exemple, on regroupe les symboles trois par trois et on les code comme suit :

symboles à coder probabilité du triplet codage du triplet longueur du code

s₁s₁s₁ 0.8³ = 0.512 0 1

s₁s₁s₂ 0.8² × 0.2 = 0.128 100 3

s₁s₂s₁ 0.8² × 0.2 = 0.128 101 3

s₂s₁s₁ 0.8² × 0.2 = 0.128 110 3

s₁s₂s₂ 0.2² × 0.8 = 0.032 11100 5

s₂s₁s₂ 0.2² × 0.8 = 0.032 11101 5

s₂s₂s₁ 0.2² × 0.8 = 0.032 11110 5

s₂s₂s₂ 0.2³ = 0.008 11111 5

Le message s₁s₁s₁s₁s₁s₂s₂s₂s₁ sera codé 010011110.

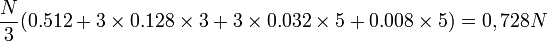
La longueur moyenne du code d'un message de N symboles est : ${N \over 3}(0.512 + 3 \times 0.128 \times 3 + 3 \times 0.032 \times 5 + 0.008 \times 5) = 0,728N$

Voir l'article détaillé : théorie des codes.

Voir aussi

Théorie algorithmique de l'information

Autorégulation

Codage de l'information

Compression de données

Projet:Sciences de l'information et des bibliothèques

Sciences de l'information et de la communication

Sciences de l'information et des bibliothèques

Technologies de l'information et de la communication

Théorème de Cox-Jaynes

Traitement de l'information

Fuite d'information

Bibliographie

Léon Brillouin Science et théorie de l'information.

Léon Brillouin Science and information theory (typographie plus lisible, mais version en anglais)

Claude Shannon A mathematical theory of communication Bell System Technical Journal, vol. 27, pp. 379-423 and 623-656, July and October, 1948 [1]

Thomas M. Cover, Joy A. Thomas. Elements of information theory, 1st Edition. New York: Wiley-Interscience, 1991. ISBN 0-471-06259-6.

(en) David MacKay, Information Theory, Inference, and Learning Algorithms, 2003 [détail des éditions]

Liens externes

(fr) Un cours de théorie de l'information par Louis Wehenkel

(fr) Un autre cours par Marie-Pierre Beal

(fr) Cours sur la théorie de l'information en pdf par Nicolas Sendrier

(fr) Cours sur la théorie de l'information par Gérard Pinson

Portail de l’informatique

Portail des mathématiques

Ce document provient de « Th%C3%A9orie de l%27information ».

Catégories : Théorie de l'information | Communication

symboles à coder	probabilité du triplet	codage du triplet	longueur du code
s₁s₁s₁	0.8³ = 0.512	0	1
s₁s₁s₂	0.8² × 0.2 = 0.128	100	3
s₁s₂s₁	0.8² × 0.2 = 0.128	101	3
s₂s₁s₁	0.8² × 0.2 = 0.128	110	3
s₁s₂s₂	0.2² × 0.8 = 0.032	11100	5
s₂s₁s₂	0.2² × 0.8 = 0.032	11101	5
s₂s₂s₁	0.2² × 0.8 = 0.032	11110	5
s₂s₂s₂	0.2³ = 0.008	11111	5

Contenu soumis à la licence CC-BY-SA. Source : Article Theorie de l'information de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Théorie de l'Information — La théorie de l information, sans précision, est le nom usuel désignant la théorie de l information de Shannon, qui est une théorie probabiliste permettant de quantifier le contenu moyen en information d un ensemble de messages, dont le codage… … Wikipédia en Français
Théorie de l'information — La théorie de l information, sans précision, est le nom usuel désignant la théorie de l information de Shannon, qui est une théorie probabiliste permettant de quantifier le contenu moyen en information d un ensemble de messages, dont le codage… … Wikipédia en Français
théorie de l'information — informacijos teorija statusas T sritis automatika atitikmenys: angl. information theory vok. Informationstheorie, f rus. теория информации, f pranc. théorie de l information … Automatikos terminų žodynas
théorie de l’information — informacijos teorija statusas T sritis fizika atitikmenys: angl. information theory vok. Informationstheorie, f rus. теория информации, f pranc. théorie de l’information, f … Fizikos terminų žodynas
Théorie de l'information quantique — Information quantique L information quantique et l informatique quantique sont deux domaines qui se jouxtent : informellement, les algorithmes Q (pour « quantiques »), par exemple l algorithme de Shor, de Grover, etc., ont été… … Wikipédia en Français
Theorie des systemes sociaux — Théorie des systèmes sociaux La théorie des systèmes sociaux est une théorie sociologique développée par le sociologue et penseur allemand Niklas Luhmann à partir des bases de la théorie de Talcott Parsons dont il a suivi les cours à Harvard… … Wikipédia en Français
information — [ ɛ̃fɔrmasjɔ̃ ] n. f. • 1274; lat. informatio I ♦ Dr. Ensemble des actes qui tendent à établir la preuve d une infraction et à en découvrir les auteurs. ⇒ instruction (préparatoire). Ouvrir une information. Information contre X. Information… … Encyclopédie Universelle
Theorie de la complexite algorithmique — Théorie algorithmique de l information La Théorie algorithmique de l information, initiée par Kolmogorov, Solomonov et Chaitin dans les années 1960, vise à quantifier et qualifier le contenu en information d un ensemble de données, en utilisant… … Wikipédia en Français
Théorie de la complexité algorithmique — Théorie algorithmique de l information La Théorie algorithmique de l information, initiée par Kolmogorov, Solomonov et Chaitin dans les années 1960, vise à quantifier et qualifier le contenu en information d un ensemble de données, en utilisant… … Wikipédia en Français
Theorie des codes — Théorie des codes En théorie de l information, la théorie des codes traite des codes et donc de leurs propriétés et leurs aptitudes à servir sur différents canaux de communication. On distingue deux modèles de communication : avec et sans… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theorie de l'information

Théorie de l'information

Sommaire

Historique

Exemples d'information

Premier exemple

Second exemple

Information imparfaite

Contenu d'information et contexte

Mesure de la quantité d'information

Quantité d'information : cas élémentaire

Quantité d'information relative à un évènement

Entropie, formule de Shannon

Codage de l'information

Voir aussi

Bibliographie

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Theorie de l'information

Théorie de l'information

Sommaire

Historique

Exemples d'information

Premier exemple

Second exemple

Information imparfaite

Contenu d'information et contexte

Mesure de la quantité d'information

Quantité d'information : cas élémentaire

Quantité d'information relative à un évènement

Entropie, formule de Shannon

Codage de l'information

Voir aussi

Bibliographie

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link