Analyse Harmonique Sur Un Espace Vectoriel Fini

En mathématiques et plus précisément dans le cadre de la théorie de l'analyse harmonique, l'analyse harmonique sur un espace vectoriel fini correspond au cas particulier où le groupe est le groupe additif d'un espace vectoriel fini.

Ce contexte s'inscrit dans celui de l'analyse harmonique sur un groupe abélien fini. Les résultats s'expriment un peu différemment car l'espace vectoriel possède des propriétés fortes, non seulement il est de dimension finie, mais son corps est nécessairement fini. Ils s'appliquent immédiatement à un corps fini car un corps fini est un espace vectoriel sur lui-même et sur son corps premier.

La théorie des codes et la cryptographie utilise largement ce cadre, par exemple pour l'étude du code dual ou l'analyse des fonctions booléennes.

Sommaire 1 Dualité de Pontryagin 1.1 Isomorphisme fondamental 1.2 Orthogonalité relativement à la dualité de Pontryagin 2 Transformée de Fourier 3 Formule sommatoire de Poisson 4 Applications 4.1 Fonction booléenne 4.2 Identité de MacWilliams 5 Notes et références 5.1 Liens externes 5.2 Références

Dualité de Pontryagin

Isomorphisme fondamental

Dans cet article V désigne un espace vectoriel de dimension finie n sur un corps fini F_q de cardinal q et de corps premier F_p où p est un nombre premier. Le symbole 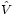désigne le groupe dual de V, χ₀ un caractère non trivial du dual du groupe additif de F_q et < | > une forme bilinéaire non dégénérée de V.

• L'application U, de V dans son dual, définie par l'égalité suivante, est un isomorphisme de groupe.

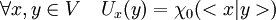
En effet, U est clairement un morphisme à valeur dans le dual de V. Montrons que l'application est injective. Soit x un élément non nul de V, il existe un élément h de V tel que < x | h > est non nul. Par linéarité sur y, l'image de l'application de V dans F_q qui à y associe < x | y > est surjective. On en déduit que U_x est un caractère non trivial, et le noyau de U est réduit à l'élément nul ce qui montre l'injectivité de U, l'égalité entre les ordres du groupe (V, +) et son dual montre la surjectivité de U et donc son caractère bijectif.

L'isomorphisme n'est pas canonique, il dépend en effet du choix de la forme bilinéaire et du caractère. Il permet néanmoins d'identifier l'algèbre du groupe V avec l'algèbre de son dual. Dans cet article, l'algèbre du groupe est noté C[V].

Le dual de V est ici celui du groupe (V, +) et non celui l'espace dual de l'algèbre linéaire.

Orthogonalité relativement à la dualité de Pontryagin

• Soit S un sous-ensemble de V, l'orthogonal de S relativement à la dualité de Pontryagin associé à (χ₀, < | >) est l'ensemble noté ici S° défini par :

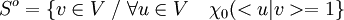
On remarque que l'orthogonal relativement à la dualité de Pontryagin ne correspond pas à l'orthogonal de la forme bilinéaire. En effet, le noyau de χ₀ n'est pas nécessairement réduit au vecteur nul.

Soit W un sous-groupe de V, les propriétés suivantes sont vérifiées :

• W° est un sous-groupe de (V, +).

• La restriction de l'isomorphisme U à W° est un isomorphisme sur l'orthogonal (au sens du groupe dual) de W.

• Si la forme bilinéaire < | >) est symétrique, alors W°° est égal à W.

Transformée de Fourier

L'ordre du groupe V est égal à n.q car V est un espace vectoriel de dimension n sur un corps de cardinal q. L'isomorphisme entre V et son dual permet de donner la définition suivante de la transformée de Fourier :

• Si u est un élément de C[V] alors sa transformée de Fourier est l'application 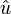de V dans C l'ensemble des nombres complexes définie par :

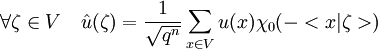
Ce résultat est l'application directe de la définition de la transformée de Fourier et du paragraphe précédent. Ici, le dual de V est identifié à V à l'aide de l'isomorphisme du paragraphe précédent.

Si ( , ) désigne le produit hermitien canonique de l'espace vectoriel complexe C[V] algèbre du groupe V, alors l'égalité suivante dite de Parseval est vérifiée :

• Le théorème de Plancherel prend la forme suivante :

Formule sommatoire de Poisson

Si W est un sous-groupe de V et v un élément de l'algèbre du groupe C[V], alors la formule sommatoire de Poisson prend la forme suivante :

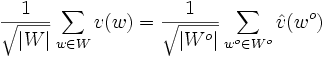
En particulier, si W est autodual, c'est-à-dire si W est confondu avec W°, alors la formule prend la forme suivante :

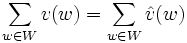
Applications

Fonction booléenne

Il existe un cas particulier, celui où l'espace vectoriel est binaire, c'est-à-dire sur le corps à deux éléments F₂. Dans ce contexte, il n'existe qu'un caractère non trivial, celui qui à l'unité associe -1. La transformée de Fourier prend alors une forme simple et porte le nom de transformée de Walsh.

Il possède de nombreuses applications en théorie des codes. Il sert par exemple en cryptographie pour assurer la sécurité d'un message à l'aide d'une boîte-S dans le cas des algorithmes à chiffrement symétrique.

Identité de MacWilliams

L'analyse harmonique sur les espaces vectoriels finis est aussi utilisée pour les codes correcteurs, particulièrement dans le contexte des codes linéaires.

L'identité de MacWilliams est un exemple, elle relie le polynôme énumérateur des poids, c'est-à-dire la distribution des poids de Hamming, d'un code linéaire et celui de son dual. Il sert pour l'étude de code comme celui de Hamming.

Notes et références

Liens externes

• (fr) Cours de code par Christine Bachoc Université de Bordeaux
• (fr) Analyse harmonique sur les groupes finis commutatifs par A. Bechata
• (fr) Mathématiques discrètes de la transformée de Fourier C. Bachoc Université de Bordeaux I

Références

• Michel Demazure Cours d'algèbre. Primalité, divisibilité, codes Cassini 1997
• FJ MacWilliams & JJA Sloane The Theory of Error-Correcting Codes North-Holland, 1977
• A. Warusfel Structures algébriques finies Hachette 1971
• G. Peyré L'algèbre discrète de la transformée de Fourier Ellipses Marketing 2004

• Portail des mathématiques