Code De Reed-Solomon

Le code de Reed-Solomon est un code correcteur basé sur les corps de Galois dont le principe est de construire un polynôme formel à partir des symboles à transmettre et de le suréchantillonner. Le résultat est alors envoyé, au lieu des symboles originaux. La redondance de ce suréchantillonnage permet au récepteur du message encodé de reconstruire le polynôme même s'il y a eu des erreurs pendant la transmission.

Sommaire 1 Vue d'ensemble 2 Histoire 3 Description intuitive 4 Propriétés 5 Applications 5.1 Stockage de données 5.2 Transmission par satellite 5.3 Transmission de données 6 Exemple 7 Faiblesse 8 Utilisation dans un modem avec codeur convolutif 9 Liens externes

Vue d'ensemble

Les codes Reed-Solomon sont des codes par bloc. En effet ils prennent en entrée un bloc de données de taille fixée, qui est transformé en un bloc de sortie de taille fixée. Ces codes travaillent sur un corps de Galois qui possède le plus souvent 2^m éléments. Le plus souvent on prend m = 8 ou m = 16. Grâce à un ajout de redondance, ces codes permettent de corriger deux types d'erreurs:

• les erreurs induisant une modification des données, ou certains bits passent de la valeur 0 à la valeur 1 et vice versa comme sur le canal binaire symétrique,
• les erreurs provoquant des pertes d'informations aussi appelé effacements, lorsque des paquets d'informations sont perdus ou effacés comme sur le canal binaire à effacement.

On note un codage de Reed-Solomon RS(n,k) ou RS(n,k,t).

Histoire

Ce code est dû à Irving S. Reed et Gustave Solomon.

Description intuitive

Imaginons un bloc de 3 nombres que l'on souhaite transmettre : 02 09 12

Ajoutons deux nombres de redondance d'information.
Le premier est la somme des 3 nombres : 02 + 09 + 12 = 23
Le second est la somme pondérée des 3 nombres, chacun est multiplié par son rang : 02×1 + 09×2 + 12×3 = 56
À la sortie du codeur, le bloc à transmettre est : 02 09 12 23 56

Suite à une perturbation, le récepteur reçoit : 02 13 12 23 56

À partir des données reçues, le décodeur calcule :
Sa somme simple : 02 + 13 + 12 = 27
Sa somme pondérée : 02×1 + 13×2 + 12×3 = 64

La différence entre la somme simple calculée (27) et celle reçue (23) indique la valeur de l'erreur : 4 (27-23 = 4)
La différence entre la somme pondérée calculée (64) et celle reçue (56), elle-même divisée par la valeur de l'erreur indique la position où l'erreur se trouve : 2 ((64-56) / 4 = 2).
Il faut donc retirer 4 au nombre du rang 2.

Le bloc original est donc 02 (13-4=09) 12 23 56

Lors d'une transmission sans perturbation, les différences des sommes simples et des sommes pondérées sont nulles.

Propriétés

La longueur maximale d’un code de Reed–Solomon est définie comme :

n = k + 2t

n = 2^m − 1

Avec :

• m : nombre de bits par symbole ;
• k : nombre de symboles d’information, appelé charge utile ;
• n: nombre de symboles transmis (charge utile et correction d'erreur) ;
• 2t : nombre de symboles de contrôle.

Si la localisation des erreurs n'est pas connue à l'avance - et c'est le cas en pratique - le codage Reed-Solomon sait corriger (n − k) / 2 erreurs.

En général, un symbole sera un octet et donc m=8 (un octet fait huit bits). Souvent, on a t = 8, n = 255 (un octet) et k = 239.

n étant souvent trop important en pratique, une partie des informations peut être remplacée par des zéros avant encodage et ne sera pas transmise, mais devra être ajoutée avant décodage. On parle dans ce cas de code Reed-Solomon raccourci (shortened Reed-Solomon codes).

Applications

Stockage de données

Pour le CD, on utilise 2 codages de Reed-Solomon, on code une première fois avec un code C1 = RS (28, 24) puis on entrelace (ceci permet de répartir l'information afin de mieux résister aux trains d'erreurs consécutives que peut provoquer une rayure qui détruit beaucoup d'octets localement) ensuite on code à nouveau les données entrelacées avec un code C2 = RS (32, 28). L'idée est que le premier code permet d'éliminer le bruit ambiant mais s'il ne peut corriger (par exemple, s'il y a une salve d'erreurs) il efface le bloc (car on peut corriger deux fois plus d'effacements que de caractères faux) et ensuite le code est désentrelacé ainsi la perte d'information est diluée sur une grande plage de données ce qui permet au code de corriger ces effacements.

Pour le DVD le principe est le même que pour les CD, on a un code PI= RS (182, 172) et un code PO = RS (208, 192)

Transmission par satellite

Pour le DVB, le codage est RS (204, 188, t=8)

Transmission de données

En ADSL/ADSL2/ADSL2plus, le codage est souvent RS (240,224,t=8) ou encore RS (255,239,t=8).

Exemple

pour le DVB, le codage sera renseigné RS (204, 188) ou encore RS (204, 188, 8)

Pour 188 (=k) octets en entrée, on ajoute 16(=2 t) octets de correction d'erreur, ce qui donne 204 en sortie du codeur.

8 octets (=t) sur 204 peuvent être corrigés.

Si plus de 8 octets sont détectés comme erronés, le bloc de données utiles est marqué comme défectueux. Aucune erreur n'est alors corrigée

Faiblesse

Suite au faible nombre de symboles que le codage Reed-Solomon peut corriger, ce codage est très mauvais en cas de bruit impulsif de longue durée, ou de bruit aléatoire régulier.

• Pour la transmission de données (ADSL, DVB-T), le bruit impulsif peut être dû à des moteurs, relais, lampes à décharge ou tubes d'éclairage, clôture électrique...
• Pour le stockage de données (CD, DVD), le bruit impulsif peut être dû à une rayure sur le support.

Utilisation dans un modem avec codeur convolutif

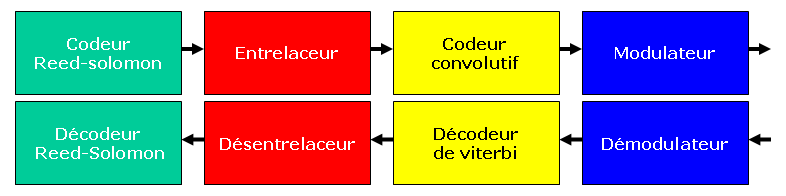
En général, en émission, dans un modem (ADSL, modem satellite IDR/SMS, DVB-S, etc ), le codage Reed-Solomon, renforcé par un entrelaceur est accompagné d'un codeur convolutif. En réception, les erreurs résiduelles non corrigées par le décodeur de Viterbi seront alors désentrelacées dans les blocs d'origines et corrigées par le décodeur Reed-Solomon dans la mesure de son pouvoir correcteur.

Le but du désentrelaceur est de remplacer en réception, une salve d'erreurs regroupées et souvent non-corrigeables (bruit impulsif) par une multitude d'erreurs réparties et souvent corrigeables pour le décodeur de Reed-Solomon.

Liens externes

• Protection algébrique des données - Code de Reed Solomon
• Code Reed-Solomon Principes et programmation du code Reed-Solomon en java
• Code CIRC (Cross Interleaved Reed-Solomon Code) Principes et programmation du code CIRC en java, F. Bernhard et M-L. Conrard
• [1] Implémentation d'un code de Reed-Solomon et d'un code CIRC (avec construction des corps finis) en langage OCaml.

• Portail des mathématiques
• Portail de l’informatique