Grand rhombicuboctaedre uniforme
- Grand rhombicuboctaedre uniforme
-
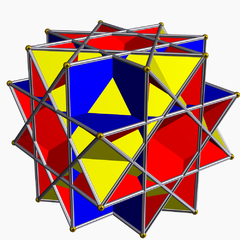
Grand rhombicuboctaèdre uniforme
En géométrie, le Grand rhombicuboctaèdre uniforme est un polyèdre uniforme non-convexe, indexé sous le nom U17.
Il partage son arrangement de sommet avec le cube tronqué convexe.
Ce solide partage son nom avec le grand rhombicuboctaèdre convexe, qui est aussi appelé le cuboctaèdre tronqué. À cause de cette confusion, le mot uniforme a été ajouté au nom de cet article.
Lien externe
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Grand rhombicuboctaedre uniforme de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Grand Rhombicuboctaèdre Uniforme — Type Polyèdre uniforme Éléments F=26, A=48, S=24 (χ=2) Faces par cotés 8{3}+(6+12){4} … Wikipédia en Français
Grand rhombicuboctaèdre uniforme — Type Polyèdre uniforme Éléments F=26, A=48, S=24 (χ=2) Faces par côtés 8{3}+(6+12){4} Configuration de … Wikipédia en Français
Grand Rhombicosidodécaèdre Uniforme — Type Polyèdre uniforme Éléments F=62, A=120, S=60 (χ=2) Faces par cotés 20{3}+30{ … Wikipédia en Français
Grand rhombicosidodecaedre uniforme — Grand rhombicosidodécaèdre uniforme Grand rhombicosidodécaèdre uniforme Type Polyèdre uniforme Éléments F=62, A=120, S=60 (χ=2) Faces par cotés 20{3}+30{ … Wikipédia en Français
Grand rhombicosidodécaèdre uniforme — Type Polyèdre uniforme Éléments F=62, A=120, S=60 (χ=2) Faces par côtés 20{3}+30{4}+12{5/2} … Wikipédia en Français
Grand Rhombicuboctaèdre — Cuboctaèdre tronqué Cuboctaèdre Tronqué Type Solide d Archimède Faces Hexagones, Octogones et Carrés Éléments : · Faces · Arêtes · Sommets · Caractéristique 26 72 48 2 … Wikipédia en Français
Grand rhombicuboctaedre — Cuboctaèdre tronqué Cuboctaèdre Tronqué Type Solide d Archimède Faces Hexagones, Octogones et Carrés Éléments : · Faces · Arêtes · Sommets · Caractéristique 26 72 48 2 … Wikipédia en Français
Grand rhombicuboctaèdre — Cuboctaèdre tronqué Cuboctaèdre Tronqué Type Solide d Archimède Faces Hexagones, Octogones et Carrés Éléments : · Faces · Arêtes · Sommets · Caractéristique 26 72 48 2 … Wikipédia en Français
Grand cubicuboctaèdre — Type Polyèdre uniforme Éléments F=20, A=48, S=24 (χ= 4) Faces par côtés 8{3}+6{4}+6{8/3} Configuration de sommet … Wikipédia en Français
Grand rhombihexaèdre — Type Polyèdre uniforme Éléments F=18, A=48, S=24 (χ= 6) Faces par côtés 12{4}+6{8/3} Configuration de sommet … Wikipédia en Français