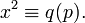Residu quadratique

Regardez d'autres dictionnaires:

• Résidu quadratique — En arithmétique modulaire, on dit qu un entier naturel q est un résidu quadratique modulo p s il existe un entier x tel que : (dans le cas contraire, on dit que q est un non résidu quadratique modulo p). En effet, un résidu quadratique… …   Wikipédia en Français

• Residu — Résidu Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un résidu peut être : En alimentaire : un sous produit des récoltes ou de la transformation des aliments, voir Valorisation de sous… …   Wikipédia en Français

• Résidu — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un résidu peut être : En alimentaire : un sous produit des récoltes ou de la transformation des aliments, voir Valorisation de sous produits… …   Wikipédia en Français

• Loi De Réciprocité Quadratique — En mathématiques, et plus précisément en théorie algébrique des nombres, la loi de réciprocité quadratique, conjecturée par Euler et Legendre et correctement démontrée pour la première fois par Gauss, établit un lien entre la résolubilité de deux …   Wikipédia en Français

• Loi de reciprocite quadratique — Loi de réciprocité quadratique En mathématiques, et plus précisément en théorie algébrique des nombres, la loi de réciprocité quadratique, conjecturée par Euler et Legendre et correctement démontrée pour la première fois par Gauss, établit un… …   Wikipédia en Français

• Loi de réciprocité quadratique — En mathématiques, et plus précisément en théorie algébrique des nombres, la loi de réciprocité quadratique, conjecturée par Euler et Legendre et correctement démontrée pour la première fois par Gauss, établit un lien entre la résolubilité de deux …   Wikipédia en Français

• Corps Quadratique — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

• Corps quadratique — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

• Corps quadratique imaginaire — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

• Entier quadratique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe, racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du terme du plus… …   Wikipédia en Français