- Élément premier
-
Idéal premier
Un idéal premier est un concept associé à la théorie des anneaux en mathématiques et plus précisément en algèbre.
Un idéal d'un anneau commutatif unitaire est dit premier si, et seulement si, le quotient de l'anneau par cet idéal est intègre.
Cette définition permet de généraliser la notion de nombre premier à des anneaux différents de celui des entiers relatifs. Ils ont un rôle important, particulièrement en théorie algébrique des nombres et plus particulièrement en arithmétique modulaire.
Sommaire
Motivations
 Ouvrage de Gauss sur l'arithmétique 1801
Ouvrage de Gauss sur l'arithmétique 1801
Arithmétique
En 1801 dans son livre Recherches arithmétiques Carl Friedrich Gauss développe des arithmétiques sur d'autres anneaux que celui des entiers relatifs. Il utilise particulièrement l'anneau des polynômes à coefficients dans un corps et l'ensemble des entiers qui portent son nom.
Ces anneaux contiennent des éléments ayant les mêmes propriétés que ceux des nombres premiers, les polynômes irréductibles ou les nombres premiers de Gauss. Cette approche est particulièrement fructueuse, elle permet par exemple de démontrer beaucoup plus simplement le théorème des deux carrés de Fermat ou une conjecture particulièrement difficile pour l'époque la loi de réciprocité quadratique.
Cette approche est généralisée aux entiers algébriques. En 1847 Gabriel Lamé (1795 1870) utilise une généralisation brutale et croit avoir démontré le grand théorème de Fermat. Ernst Kummer (1810 1893) montre que l'unicité associé au théorème de décomposition en facteurs premiers n'est plus assurée. Il développe les nombres complexes idéaux pour retrouver une unicité à travers un nouveau concept.
Ce concept ayant pour objectif de pallier les insuffisances des propriétés des nombres, est formalisé par la notion d'idéal, à la suite des travaux de Richard Dedekind (1831 1916). Il existe plusieurs propriétés pour caractériser les différents idéaux. Un idéal premier correspond au nombre premier. Dans les cas simples, où l'idéal est associé à un nombre, par exemple parce que l'anneau est principal ou factoriel, les notions coïncident. Les nombres premiers, définis usuellement par le fait que dans toute décomposition en deux facteurs, l'un au moins est un élément inversible, correspondent alors à un idéal premier. Dans les cas plus complexes, comme les anneaux de Dedekind, le concept d'idéal premier reste opérationnel, alors que celui de nombre premier perd largement sa puissance opératoire.
Géométrie algébrique
Une variété algébrique est l'objet de base de la géométrie algébrique. Elle correspond à une géométrie définie par des équations algébriques. Un des objets de la géométrie algébrique est le classement des différentes variétés. La notion d'idéal premier est à la base de ces classements.
De même qu'un polynôme peut être vu sous l'angle d'un idéal de l'anneau des polynômes, une variété algébrique peut être définie par l'idéal des polynômes qui s'annulent sur cette variété. Une variété est alors parfaitement classée par la données des idéaux premiers de polynômes qui s'annulent sur elle.
L'association de la géométrie et de l'arithmétique ouvre la voie à la démonstration de nombreux théorèmes. Elle est, par exemple, à la base de la démonstration du grand théorème de Fermat par Andrew Wiles en 1994.
Définition
Dans toute la suite de l'article, A désigne un anneau commutatif unitaire, a un élément de A et I un idéal de A.
-
- Un idéal I de A est dit premier si, et seulement si, le quotient de A par I est intègre et qu'il est différent de l'anneau réduit à l'élément nul.
On peut exprimer cette définition à l'aide de la condition suivante : un idéal I de A est premier si et seulement si c'est un idéal propre (différent de A) et si
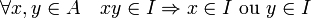
En effet
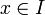 dans A est équivalent à x = 0 dans le quotient A / I.
dans A est équivalent à x = 0 dans le quotient A / I.-
- Un élément a de A est dit premier si, et seulement si l'idéal a.A est premier.
Cette définition généralise la notion de nombre premier, tout en conservant les propriétés. Ainsi si un élément p est premier, alors toute décomposition de p en deux facteurs contient un élément inversible.
Exemples
Entiers relatifs
Dans Z, un entier premier au sens de la définition précédente est un entier tel que Z/n Z soit intègre. Tout anneau de cardinal fini intègre est un corps. En conséquence soit n est un nombre premier au sens usuel, soit -n est un nombre premier.
La définition de l'article correspond à la définition usuelle aux inversibles près. En effet, par convention, un nombre premier est l'élément associé positif des générateurs de l'idéal. Cette convention permet une expression plus simple du théorème fondamental de l'arithmétique (cf l'article élément inversible).
Polynôme
Polynôme à coefficient dans un corps
Dans le cas où les polynômes sont à coefficient dans un corps, l'anneau est, comme précédemment euclidien, donc principal : tout idéal est composé des multiples d'un polynôme unitaire. Un polynôme est premier si, et seulement s'il est différent d'une constante et si toute décomposition en deux facteurs contient un élément inversible.
Cette définition est équivalente à celle d'élément irréductible. Cet état de fait est général dans les anneaux principaux. La tradition impose surtout de parler de polynôme irréductible.
Polynôme à coefficient dans Z
Si les coefficients du polynôme sont choisis dans Z, alors l'anneau des polynômes n'est plus principal. Par exemple, l'idéal I engendré par X et 2 n'est pas principal. Le quotient de Z[X] par I est un anneau à deux éléments donc intègre. Cet idéal est premier, mais n'est pas associé à un élément de l'anneau.
Entier de Gauss
Les entiers de Gauss forment un anneau euclidien. À chaque idéal correspond une classe d'association engendrant l'idéal, les notions d'idéaux et de nombres premiers de Gauss coïncident. Les éléments premiers s'appellent des nombres premiers de Gauss.
Propriétés
Lemme d'Euclide
La traduction du lemme d'Euclide est directe en termes d'idéal:
-
- Un idéal I est premier si, et seulement si, la proposition suivante est vérifiée:
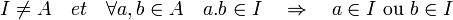
Cette proposition s'exprime aussi de la manière suivante :
-
- Si un idéal premier I contient le produit de deux idéaux A et B, il contient soit A soit B.
Cette proposition est l'équivalent du lemme d'Euclide : si un nombre premier divise le produit a.b alors il divise soit a soit b.
Démonstration- Si I est un idéal premier :
Alors le quotient de A par I est différent de l'anneau réduit à l'élément nul, et I est nécessairement différent de A. De plus, dire que
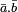 est nul, revient à dire que soit
est nul, revient à dire que soit  soit
soit 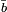 est nul car le quotient est intègre. Cette assertion est équivalente à dire que soit a soit b est un élément de I.
est nul car le quotient est intègre. Cette assertion est équivalente à dire que soit a soit b est un élément de I.- Réciproquement :
Comme I est différent de A, le quotient est différent de l'anneau réduit à l'élément nul. Si un produit
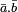 est nul dans le quotient alors a.b est un élément de I, donc soit a soit b est élément de I. Ce qui revient à dire que soit
est nul dans le quotient alors a.b est un élément de I, donc soit a soit b est élément de I. Ce qui revient à dire que soit  soit
soit 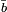 est nul, c'est la définition de l'intégrité dans un anneau.
est nul, c'est la définition de l'intégrité dans un anneau.-
- Si un idéal premier I contient le produit de deux idéaux A et B il est contient soit A soit B :
Supposons que I ne contienne ni A ni B, alors il existe a (resp. b) élément de A (resp. de B) non élément de I. Alors a.b est un élément de A.B qui ne peut être élément de I car I est premier. La contraposée permet de conclure.
Anneau principal
Si A est principal, un idéal premier ressemble à l'idée intuitive que l'on s'en fait. C'est par exemple de cas des entiers relatifs.
-
- Si A est principal les propositions suivantes sont équivalentes :
Démonstration-
- (i) ⇒ (ii)
Soit un idéal I engendré par p, dire qu'un produit a.b est élément de I revient à dire que p divise a.b. La proposition précédente permet de conclure.
-
- (ii) ⇒ (iii)
Soit a et b deux éléments de A tel que p = a.b, alors (ii) nous apprend que p divise soit a soit b, en conséquence p est égal soit à a soit à b et l'autre élément est une unité.
-
- (iii) ⇒ (iv)
Soit I l'idéal engendré par p. Considérons un idéal contenant I, il est engendré par un diviseur de p, donc par 1 ou par lui-même. En conséquence, les seuls idéaux contenant I sont lui-même et A, ce qui est la définition d'un idéal maximal.
-
- (iv) ⇒ (i)
Supposons que I soit maximal et soit a et b deux éléments de A tel que
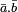 soit nul. Alors l'idéal engendré par a (respectivement b) contient I, il est soit égal à I soit à A, car I est maximal. Les deux idéaux engendrés par a et b ne peuvent simultanément être égal à A, sinon l'idéal engendré par a.b serait égal à A donc un des deux idéaux est égal à I, ce qui montre que soit
soit nul. Alors l'idéal engendré par a (respectivement b) contient I, il est soit égal à I soit à A, car I est maximal. Les deux idéaux engendrés par a et b ne peuvent simultanément être égal à A, sinon l'idéal engendré par a.b serait égal à A donc un des deux idéaux est égal à I, ce qui montre que soit  soit
soit 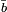 est nul. Et le quotient est intègre.
est nul. Et le quotient est intègre.Voir aussi
Liens externes
- (fr) Idéaux, anneaux quotients par les-mathématiques.net
- (fr) Anneau et corps par Christian Squarcini
- (en) Prime Ideal sur planetmath.org
Références
- S. Lang Algebre Dunod 2004
- D. Perrin Cours d'algèbre Ellipse 1996
- S. Mac Lane & G. Birkhoff ; Algèbre [détail des éditions]
- Portail des mathématiques
Catégorie : Idéal -
Wikimedia Foundation. 2010.