Endomorphisme nilpotent

Endomorphisme nilpotent
Exemple d'image d'une base par un endomorphisme nilpotent en dimension 3.

Un endomorphisme nilpotent est un morphisme d'un objet mathématique sur lui-même, qui, composé par lui-même un nombre suffisant de fois, donne le morphisme nul. C’est donc (lorsque les endomorphismes de cet objet forment un anneau) un élément nilpotent de cet anneau.

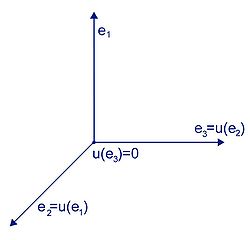
En algèbre linéaire, on considère les endomorphismes nilpotents d’un espace vectoriel. Un exemple est donné dans l'illustration. Ils interviennent dans la réduction des endomorphismes, c’est-à-dire la représentation d'un endomorphisme quelconque sous une forme la plus simple possible. Cette réduction sert par exemple pour la résolution d'équations différentielles linéaires.

On retrouve également le concept de nilpotence dans l'étude des groupe de Lie, avec l'analyse des algèbres de Lie nilpotentes.

Les endomorphismes nilpotents d'un espace vectoriel sont l'objet principal de cet article. Lorsque de plus cet espace est de dimension finie, chacun de ses endomorphismes est représenté par une matrice (dans une base de l'espace vectoriel concerné). L'endomorphisme est alors nilpotent si et seulement s'il a une matrice nilpotente, ce qui, par le calcul, permet une approche plus concrète du concept (toutes les propriétés générales des endomorphismes nilpotents ont leur pendant dans le contexte plus particulier des matrices nilpotentes), et offre d'importantes applications pratiques.

Sommaire

Définition

Soit E un espace vectoriel sur un corps K et u un endomorphisme de E. L'endomorphisme u est dit nilpotent si et seulement s'il existe un entier n>0 tel que un = 0. Le plus petit entier naturel n vérifiant cette propriété est alors appelé indice (de nilpotence) de l'endomorphisme u.

Soit x un vecteur de E, on appelle indice de x (pour l'endomorphisme nilpotent u) le plus petit entier naturel p tel que up(x) = 0.

Un sous-espace cyclique de E (pour l'endomorphisme nilpotent u) est un sous-espace vectoriel de E engendré par une famille de la forme (x, u(x), u2(x), ..., up-1(x)), où x est un vecteur d'indice p.

Intérêt du concept

Nilpotence et réduction

Un enjeu important en mathématique est celui de la réduction, c’est-à-dire de la décomposition d'un concept en sous-concepts plus simples et qui décrivent l'intégralité du concept initial. Dans le cadre des applications linéaires la réduction est traitée dans l'article réduction d'endomorphisme. En dimension finie, les endomorphismes nilpotents jouent un rôle important dans le cas où \mathbb K\; est un corps algébriquement clos. Un corps est dit algébriquement clos si et seulement si tous les polynômes sont scindés, autrement dit si tous les polynômes s'écrivent comme produit de polynômes du premier degré. C'est par exemple le cas pour les nombres complexes. Sous cette hypothèse, la théorie de la réduction d'endomorphisme montre que le cas général se résume à la somme d'un endomorphisme diagonalisable et d'un nilpotent. Ce résultat est connu sous le nom de Décomposition de Dunford.

Si le corps n'est pas algébriquement clos, alors il est toujours possible d'étendre l'espace vectoriel sur un corps algébriquement clos. Cette technique est largement utilisée. Pour les réels, la physique n'utilise pratiquement que cette approche.

Applications

Puisqu'il est possible d'étendre à la clôture algébrique, la réduction des endomorphismes dans ce contexte joue un rôle essentiel en mathématique. Les endomorphismes nilpotents sont donc nécessaires à divers branches des mathématiques. En algèbre linéaire, ils interviennent naturellement dans la réduction de Jordan qui correspond à un cas important de réduction des endomorphismes. Les techniques utilisées sont celles des polynômes d'endomorphismes. Les conséquences se retrouvent sur la résolution de systèmes d'équations linéaires, dans la résolution d'équations différentielles linéaires où ils apparaissent comme des cas limites. En mathématiques appliquées, ils sont importants pour la recherche d'algorithmes, on utilise alors essentiellement les matrices nilpotentes où des représentations simples sont alors nécessaires.

Propriétés

L'exemple illustre l'essentiel des propriétés des endomorphismes nilpotents. On y trouve des propriétés sur l'indice des endomorphismes et des vecteurs, des conditions nécessaires et suffisantes grâce aux polynômes. Des réductions avec une décomposition en espaces propres et l'existence d'une base réduite. Il existe aussi des propriétés calculatoires des matrices nilpotentes traitées dans l'article Matrice nilpotente.

Nilpotence et indice

L'indice d'un endomorphisme nilpotent possède deux grandes propriétés :

  • L'indice d'un endomorphisme nilpotent est inférieur ou égal à la dimension de l'espace (pour la démonstration penser à utiliser la suite (kerfn)).
  • Il existe un vecteur dont l'indice est celui de l'endomorphisme.

Nilpotence et polynômes en dimension finie

Les polynômes fournissent non seulement des conditions nécessaires et suffisantes pour la nilpotence, mais renseignent de plus sur l'indice.

  • Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à ( − X)n où n est la dimension de l'espace.
  • Un endomorphisme est nilpotent si et seulement si son polynôme minimal est égal à Xp où p est l'indice de l'endomorphisme.
  • Le polynôme minimal d'un vecteur x est égal à X^{p_x}\; où px est l'indice du vecteur x.

Nilpotence et réduction en dimension finie

Le principe de réduction consiste à trouver une décomposition en somme directe de sous-espaces stables de l'espace vectoriel. Il en existe une pour les endomorphismes nilpotents. Et elle est compatible avec la réduction de Jordan. Cette approche est générale à l'analyse des endomorphismes. Dans le cas des endomorphismes nilpotents, elle est intimement liée à la notion de base réduite. Tout endomorphisme nilpotent u d'un espace vectoriel E non réduit au vecteur nul vérifie les propriétés suivantes :

  • Si x\; est un vecteur d'indice p alors la famille (x, u(x),...u^{p-1}(x))\; est libre. C'est donc une base du sous-espace cyclique qu'elle engendre.
  • Pour tout sous-espace stable F de E (en particulier pour tout sous-espace cyclique), l'endomorphisme de F obtenu par restriction de u est, lui aussi, nilpotent (donc vérifie toutes les propriétés de cette liste, dès que F n'est pas réduit au vecteur nul).
  • u possède une unique valeur propre : 0 (en particulier, son noyau n'est pas réduit au vecteur nul).
  • E est somme directe de sous-espaces cycliques non réduits au vecteur nul.
  • Une telle décomposition est "maximale", au sens où toute autre décomposition de E en somme directe de sous-espaces stables non réduits au vecteur nul est constituée d'au plus autant de sous-espaces.
Démonstration
  • Un endomorphisme u est nilpotent si et seulement si son polynôme minimal est égal à Xp où p est l'indice de l'endomorphisme.

Par définition de la nilpotence, Xp est un polynôme annulateur de l'endomorphisme u, et ce n'est le cas d'aucun de ses diviseurs stricts. Comme \mathbb K[X] est un anneau euclidien, et donc qu'il vérifie l'identité de Bezout, le polynôme unitaire Xp divise tous les polynômes annulateurs de u : on dit que Xp est le polynôme minimal de u. De la même façon X^{p_x} où px est l'indice du vecteur x, est le plus petit polynôme unitaire au sens de la divisibilité qui, appliqué à u, annule x, c'est-à-dire le polynôme minimal de x. Cela a pour conséquence immédiate qu'aucun polynôme de u non nul de degré strictement inférieur à px n'annule x, ce qui se traduit sur l'espace vectoriel par :

  • Si x est un vecteur d'indice px alors la famille (x, u(x),...u^{p_x-1}(x)) est une famille libre.
  • Il existe toujours un vecteur dont l'indice est celui de l'endomorphisme.

En effet le polynôme minimal d'un vecteur divise le polynôme minimal de l'endomorphisme, donc est un Xk, pour k ≤ p, et si aucun n'était de degré p, Xp − 1 annulerait u.

  • L'indice d'un endomorphisme nilpotent est toujours inférieur ou égal à la dimension de l'espace.

Cette proposition est une conséquence directe des deux résultats précédents.

  • E est somme directe de sous-espaces cycliques (que l'on peut alors supposer tous différents de {0}, quitte "gommer" de cette somme les sous-espaces égaux à {0}).

Démontrons ce résultat par récurrence sur l'indice p de l'endomorphisme.

Si p est égal à 1, l'endomorphisme est nul et le résultat est trivial.

Supposons le résultat vrai pour p et démontrons le pour p+1. Soit u un endomorphisme d'indice p+1. Considérons alors la restriction de u à u(E). C'est un endomorphisme nilpotent d'indice p. Par hypothèse de récurrence, u(E) est somme directe de sous-espaces cycliques Fi pour i appartenant à un certain ensemble I d'indices. Chaque Fi admet une base de la forme (y_i, u(y_i), \cdots, u^{p_i-1}(y_i)), où yi est un vecteur d'indice pi de u(E), donc yi=u(xi) pour un vecteur xi d'indice pi+1 de E.

La famille (u^{j+1}(x_i))_{i\in I, 0\le j<p_i}=(u^j(y_i))_{i\in I, 0\le j<p_i} étant une base de u(E), la sous-famille (u^{p_i}(x_i))_{i\in I} est libre. Comme les vecteurs de cette sous-famille libre appartiennent au noyau de u, on peut compléter celle-ci en une base de ce noyau, en rajoutant des vecteurs que l'on notera (x_i)_{i\in J} (pour un ensemble J d'indices supplémentaires). Puisque ces nouveaux vecteurs sont des vecteurs non nuls du noyau, ils sont d'indice 1. Posons (pour uniformiser les notations) pi = 0 pour i\in J : ainsi, pour tout indice i\in K=I\cup J, xi est d'indice pi + 1.

Montrons que E est la somme directe des sous-espaces cycliques associés à tous ces xi, c'est-à-dire montrons que (u^j(x_i))_{i\in K, 0\le j\le p_i} est une base de E. Cette famille est constituée de (u^j(x_i))_{i\in I, 0\le j<p_i}, dont l'image par u est une base de u(E), et de (u^{p_i}(x_i))_{i\in K}, qui est une base du noyau. La conclusion souhaitée en résulte (voir l'article théorème du rang).

  • La restriction de u à Ei est de noyau non réduit au vecteur nul et possède une unique valeur propre 0. Cette propriété reste vraie pour l'endomorphisme lui-même.

La restriction de u à Ei est un endomorphisme nilpotent, son polynôme minimal est une puissance de X, la seule valeur propre est 0 et comme 0 est valeur propre, le noyau est non nul. Ce raisonnement s'applique aussi à u sur l'espace vectoriel entier, ce qui démontre la fin de la proposition.

  • Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à ( − X)n où n est la dimension de l'espace.

La seule valeur propre est 0, donc sur sa clôture algébrique, le polynôme caractéristique est scindé et possède pour racine uniquement 0. Ce polynôme est donc une puissance de X, et de degré n. Son signe provient du signe du monôme de plus haut degré de tous les polynômes caractéristiques.

Applications en mathématiques

Matrice nilpotente

Les résultats théoriques obtenus à l'aide de l'analyse des endomorphismes nilpotents ont des conséquences importantes sur les matrices nilpotentes. Ces résultats sont traités dans l'article Matrice nilpotente.

Réduction des endomorphismes

Dans le cas où le corps est algébriquement clos et en dimension finie, les endomorphismes nilpotents jouent un rôle particulier dans la problématique de la réduction des endomorphismes. Le cas général, celui où toutes les racines du polynôme minimal sont simples, correspond aux endomorphismes diagonalisables. Ce cas génère un ensemble d'endomorphismes partout dense. En revanche, en cas de racine multiple, alors il existe une composante nilpotente.

Cette décomposition joue un rôle important dans les calculs que l'on observe dans l'univers des matrices. Elle permet par exemple de prouver que toute matrice est trigonalisable et offre une forme particulièrement simple en bloc de Jordan.

De nombreux algorithmes relèvent directement de cette décomposition. Elle permet d'accélérer massivement la résolution d'un système d'équations linéaires.

Équation différentielle linéaire

La réduction de Jordan joue un rôle particulier pour les équations différentielles linéaires. Par exemple, dans le cas où les coefficients sont constants, alors le calcul de l'exponentielle d'une matrice dans le cas général est largement plus simple dans le cas d'une représentation matricielle réduite par la méthode de Jordan. Il est alors important de pouvoir calculer l'exponentielle d'une matrice nilpotente. Ce cas est exposé dans l'article Matrice nilpotente.

Groupes de Lie

Dans l'étude des groupes de Lie, on s'intéresse parfois à ce que l'on appelle groupes de Lie nilpotents. Comme pour tout groupe de Lie, leur structure est décrite par leur fibré tangent, qui est muni d'une structure d'algèbre de Lie. Les représentations de ces algèbres dans les endomorphismes s'obtiennent à partir d'endomorphismes nilpotents.

Sources

Liens internes

principaux articles utilisés pour les démonstrations

Principaux articles utilisant la notion d'endomorphisme nilpotent

v · d · m
Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs Famille génératrice • Famille libre (indépendance linéaire) • Base • Théorème de la base incomplète • Rang • Colinéarité Mathématiques
Sous-espace Sous-espace vectoriel • Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Diagonalisation • Endomorphisme nilpotent
En dimension finie Espace vectoriel de dimension finie • Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford • Décomposition de Frobenius
Enrichissements de structure Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

Liens externes

Références

  • Serge Lang Algèbre Dunod

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Endomorphisme nilpotent de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Endomorphisme Nilpotent — Exemple d image d une base par un endomorphisme nilpotent en dimension 3. Un endomorphisme nilpotent est un morphisme d un objet mathématique sur lui même, qui, composé par lui même un nombre suffisant de fois, donne l application nulle. Un… …   Wikipédia en Français

  • Endomorphisme Linéaire — En mathématiques, un endomorphisme linéaire ou endomorphisme d espace vectoriel ou endomorphisme est une application linéaire d un espace vectoriel E dans lui même. L ensemble des endomorphismes d un espace vectoriel E est habituellement noté… …   Wikipédia en Français

  • Endomorphisme lineaire — Endomorphisme linéaire En mathématiques, un endomorphisme linéaire ou endomorphisme d espace vectoriel ou endomorphisme est une application linéaire d un espace vectoriel E dans lui même. L ensemble des endomorphismes d un espace vectoriel E est… …   Wikipédia en Français

  • Endomorphisme linéaire — En mathématiques, un endomorphisme linéaire ou endomorphisme d espace vectoriel est une application linéaire d un espace vectoriel dans lui même. L ensemble des endomorphismes d un espace vectoriel E est habituellement noté End(E) ou . L ensemble …   Wikipédia en Français

  • Réduction d'endomorphisme — En mathématiques, et plus particulièrement en algèbre linéaire, la réduction d endomorphisme est une technique mathématique qui a pour objectif d exprimer des matrices et des endomorphismes sous une forme plus simple, notamment pour faciliter les …   Wikipédia en Français

  • Reduction d'endomorphisme — Réduction d endomorphisme En mathématiques, et plus particulièrement en algèbre linéaire, la réduction d endomorphisme est une technique mathématique qui a pour objectif d exprimer des matrices et des endomorphismes sous une forme plus simple,… …   Wikipédia en Français

  • Polynome d'endomorphisme — Polynôme d endomorphisme En algèbre linéaire, on utilise fréquemment la notion de polynôme d endomorphisme (ou de matrice), qui est une combinaison linéaire de puissances (au sens de la composition de fonctions) de l endomorphisme. Pour un… …   Wikipédia en Français

  • Polynôme d'endomorphisme — En algèbre linéaire, on utilise fréquemment la notion de polynôme d endomorphisme (ou de matrice), qui est une combinaison linéaire de puissances (au sens de la composition de fonctions) de l endomorphisme. Pour un endomorphisme u d un espace… …   Wikipédia en Français

  • Polynome minimal d'un endomorphisme — Polynôme minimal d un endomorphisme Le polynôme minimal est un outil qui permet d utiliser des résultats de la théorie des polynômes à l algèbre linéaire. Il est en effet possible d appliquer un polynôme à un endomorphisme, comme expliqué dans l… …   Wikipédia en Français

  • Polynôme minimal d'un endomorphisme — Le polynôme minimal est un outil qui permet d utiliser des résultats de la théorie des polynômes à l algèbre linéaire. Il est en effet possible d appliquer un polynôme à un endomorphisme, comme expliqué dans l article intérêt du concept de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”