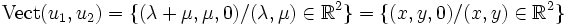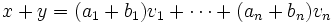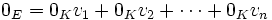Sous-espace vectoriel engendre

Sous-espace vectoriel engendre

Sous-espace vectoriel engendré

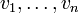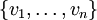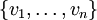Étant donnés un espace vectoriel sur un corps commutatif \mathbb{K}, des vecteurs v_1, \ldots, v_n de E, le sous-espace vectoriel engendré par les vecteurs est l'ensemble des combinaisons linéaires de ces vecteurs. C'est un sous-espace vectoriel de E appelé sous-espace vectoriel engendré par le système de vecteurs \{v_1,\ldots, v_n\}, c'est le plus petit sous-espace vectoriel de E contenant \{v_1,\ldots, v_n\}.

Sommaire

Définitions

Sous espace vectoriel engendré par une famille finie de E

Étant donnés un espace vectoriel sur un corps commutatif 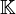\mathbb{K}, un entier naturel non nul n, et une famille de n vecteurs 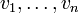v_1, \ldots, v_n de E, le sous-espace vectoriel engendré par la famille, noté 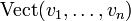{\rm Vect}(v_1, \ldots, v_n), est l'ensemble :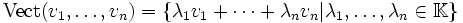

{\rm Vect}(v_1, \ldots, v_n) = \left\{\lambda_1 v_1+\cdots+\lambda_n v_n | \lambda_1,\ldots, \lambda_n\in \mathbb{K}\right\}

C'est un sous-espace vectoriel F de E appelé sous-espace vectoriel engendré par la famille 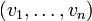(v_1,\ldots, v_n). On dit que la famille 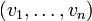(v_1, \ldots, v_n) est une famille génératrice ou qu'elle « engendre » F.

On peut dire aussi que l'ensemble 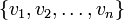\{v_1, v_2,\ldots, v_n\} est un système générateur de F ou un système de générateurs de F.

Sous espace vectoriel engendré par une partie de E

La notion se généralise à une famille quelconque (v_i)_{i\in I} de vecteurs de E. Le sous-espace vectoriel engendré par la famille est l'ensemble de toutes les combinaisons linéaires finies de vecteurs de la famille, noté {\rm Vect}\left((v_i)_{i\in I}\right), est :

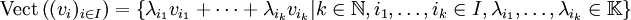
{\rm Vect}\left((v_i)_{i\in I}\right) = \left\{ \lambda_{i_1} v_{i_1} + \cdots + \lambda_{i_k} v_{i_k} | k \in \mathbb{N}, i_1, \ldots, i_k \in I, \lambda_{i_1} ,\ldots, \lambda_{i_k} \in \mathbb{K} \right\}

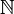où \mathbb{N} est l'ensemble des entiers naturels.

Une famille quelconque de vecteurs de E peut-être considérée comme un sous-ensemble A de l'espace vectoriel E. Le sous-espace vectoriel engendré par A est donc l'ensemble de toutes les combinaisons linéaires (finies) d'éléments de A. Il est noté Vect(A) ou parfois < A >  :

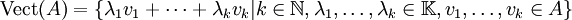
\mathrm{Vect}(A) = \left\{ \lambda_1 v_1 + \cdots + \lambda_k v_k | k \in \mathbb{N}, \lambda_1 ,\ldots, \lambda_k \in \mathbb{K}, v_1 ,\ldots, v_k \in A \right\}

Remarquez que le nombre de vecteurs intervenant dans la combinaison linéaire peut varier, de zéro à un certain entier, mais pas jusqu'à l'infini. La partie A est appelée partie génératrice de Vect(A).

Remarques

L'ensemble engendrant un sous-espace vectoriel n'est pas nécessairement une partie basique (c'est-à-dire une base) de F de même que les vecteurs de l'ensemble n'ont pas besoin d'être linéairement indépendants. D'autre part, un ensemble minimal engendrant le sous-espace vectoriel F est une base de F. Autrement dit un ensemble engendrant un espace vectoriel F est une base de celui-ci si et seulement si tout vecteur de F peut être écrit de manière unique comme combinaison linéaire des éléments de l'ensemble.

Exemples

  • L'espace vectoriel réel 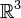\mathbb{R}^3 admet {(1,0,0),(0,1,0),(0,0,1)} comme ensemble générateur, qui est aussi une base. Un autre ensemble générateur est {(1,2,3),(0,1,2),( − 1,1 / 2,3),(1,1,1)} mais celui-ci n'est pas une base de 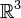\mathbb{R}^3 parce que les vecteurs sont linéairement dépendants. L'ensemble {(1,0,0),(0,1,0),(1,1,0)} n'engendre pas 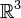\mathbb{R}^3; au lieu de cela il engendre le sous-espace vectoriel constitué de tous les vecteurs de 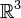\mathbb{R}^3 dont la dernière composante est nulle.
  • Dans l'espace vectoriel usuel, 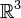\mathbb{R}^3, considérons les vecteurs u1 = (1,0,0) et u2 = (1,1,0). On a
{\rm Vect}(u_1, u_2)=\{(\lambda+\mu,\mu,0)/(\lambda,\mu)\in\mathbb{R}^2\}=\{(x,y,0)/(x,y)\in\mathbb{R}^2\}
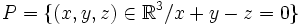  • Soit P=\{(x,y,z)\in\mathbb{R}^3/x+y-z=0\}. On a
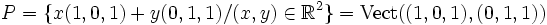P=\{x(1,0,1)+y(0,1,1)/(x,y)\in\mathbb{R}^2\}={\rm Vect}((1,0,1),(0,1,1)).

Théorèmes

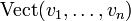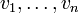Théorème 1: {\rm Vect}(v_1, \ldots, v_n) est un sous-espace vectoriel de E. De plus, cet espace vectoriel est le plus petit sous-espace vectoriel de E contenant les vecteurs v_1, \ldots, v_n.

Ce résultat (qui est démontré un peu plus loin dans cette section) est une des raisons pour lesquelles la notion de sous-espace vectoriel engendré est importante.

Théorème 2: Vect(A) est aussi un sous-espace vectoriel de E. De plus, cet espace vectoriel est le plus petit sous espace-vectoriel de E, contenant A.

Nous n'allons démontrer que le théorème 1. La démonstration du théorème 2 est très similaire, mais un peu plus malaisée à rédiger, puisque les vecteurs de toute combinaison linéaire donnée peuvent être différents.

Démonstration du théorème 1:

Stabilité pour la somme:

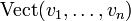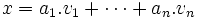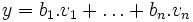Les formes les plus générales possibles pour deux éléments de {\rm Vect}(v_1, \ldots, v_n) sont x=a_1.v_1+\cdots+a_n.v_n et y=b_1.v_1+\ldots+b_n.v_n.

Nous avons à montrer que x + y est aussi une combinaison linéaire de ces vecteurs. En utilisant l'associativité et la commutativité de l'addition ainsi que la distributivité, nous pouvons écrire:

x + y = ( a_1 + b_1 ) v_1 + \cdots + ( a_n + b_n ) v_n \,

et puisque pour tout i, ai + bi est un scalaire de K, nous voyons que x + y est effectivement une combinaison linéaire des vecteurs donnés.

Stabilité pour la multiplication par un scalaire:

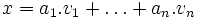Soit c un scalaire et à nouveau considérons une combinaison linéaire de la forme: x=a_1.v_1+\ldots+a_n.v_n.

Nous avons à montrer que c.x est aussi une combinaison linéaire de ces vecteurs.

Nous avons

c x = ( c a_1 ) v_1 + \cdots + ( c a_n ) v_n \,

et puisque pour tout i, c.ai est aussi un scalaire le résultat est acquis.

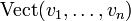{\rm Vect}(v_1, \ldots, v_n) est non vide.

Le vecteur nul de E, 0E est une combinaison linéaire de 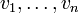v_1, \ldots, v_n puisque nous pouvons écrire:

0_E=0_Kv_1+0_Kv_2+\cdots+0_Kv_n\,

(Ici, 0K est l'élément neutre additif du corps K.)

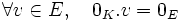Cette dernière relation est bien vraie, parce que dans tout espace vectoriel nous avons \forall v\in E,\quad 0_K.v=0_E.

Minimalité:

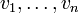Supposons que F soit un autre sous-espace vectoriel de E contenant les vecteurs v_1, \ldots, v_n.

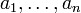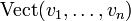Alors F est stable pour la multiplication et l'addition des vecteurs, ainsi nous pouvons démontrer par une récurrence finie sur le nombre de vecteurs que pour tous scalaires a_1, \ldots, a_n, a_1.v_1+\cdots+a_n.v_n est un élément de F. Ainsi, {\rm Vect}(v_1, \ldots, v_n), l'ensemble de telles combinaisons linéaires est une sous-ensemble de F.

Propriétés

  • Soient 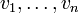v_1, \ldots, v_n n vecteurs d'un espace vectoriel E. Nous avons
\textrm{Vect}(v_1, \ldots, v_{n-1}) = \textrm{Vect} (v_1, \ldots, v_n) \Longleftrightarrow v_n \in \textrm{Vect}(v_1, \ldots, v_{n-1})
  • La dimension d'un espace vectoriel engendré par une famille de n vecteurs est égale à n si et seulement si la famille est libre.
  • Pour toutes parties A et A' de E,
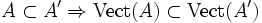
    • A\subset A'\Rightarrow {\rm Vect}(A)\subset {\rm Vect}(A')
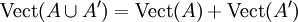    • {\rm Vect}(A\cup A')={\rm Vect}(A)+{\rm Vect}(A').
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Sous-espace vectoriel engendr%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sous-espace vectoriel engendre de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Sous-espace vectoriel engendré — Etant donnée une partie (pas nécessairement finie) A d un espace vectoriel E sur un corps commutatif K, le sous espace vectoriel engendré par A est exactement le plus petit sous espace vectoriel de E contenant A. Des définitions équivalentes sont …   Wikipédia en Français

  • Sous-espace vectoriel — En algèbre linéaire, étant donné un espace vectoriel E sur un corps K, un sous espace vectoriel de E est une partie non vide F de E stable par combinaisons linéaires. Autrement dit, cette partie doit vérifier : La somme vectorielle de deux… …   Wikipédia en Français

  • Espace vectoriel — En algèbre linéaire, un espace vectoriel est un ensemble muni d une structure permettant d effectuer des combinaisons linéaires. Étant donné un corps K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée +) muni d une… …   Wikipédia en Français

  • Espace vectoriel normé — Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très… …   Wikipédia en Français

  • Sous-espace projectif — En géométrie projective, un sous espace projectif est défini comme le projeté d un sous espace vectoriel de l espace vectoriel associé. Contrairement à ce qui se passe en géométrie affine, les propriétés sur les dimensions règlent de nombreux… …   Wikipédia en Français

  • Sous-espace supplementaire — Sous espace supplémentaire En mathématiques, un sous espace supplémentaire est un sous espace vectoriel défini par rapport à un autre sous espace qui, de manière intuitive (ne pas confondre avec la notion de complémentaire), sépare l espace en… …   Wikipédia en Français

  • Espace Vectoriel Normé — Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très… …   Wikipédia en Français

  • Espace vectoriel norme — Espace vectoriel normé Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach,… …   Wikipédia en Français

  • Sous-espace stable — En algèbre linéaire, un endomorphisme laisse stable un sous espace vectoriel F quand les éléments de F ont pour image un élément de F. La recherche de sous espaces stables est étroitement liée à la théorie de la réduction des endomorphismes.… …   Wikipédia en Français

  • Sous-espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”