Groupe Nilpotent

Groupe Nilpotent

Groupe nilpotent

En théorie des groupes, un groupe est dit nilpotent lorsqu'il possède une certaine propriété : intuitivement, on peut penser qu'on peut rendre le groupe abélien par l'utilisation répétée du commutateur [x,y] = xyx − 1y − 1 . Les groupes nilpotents apparaissent naturellement en théorie de Galois ou pour la classification des groupes de Lie ou des groupes algébriques linéaires.

Sommaire

Définition

Soit G un groupe noté multiplicativement, d'élément neutre e. Si A et B sont deux sous-groupes de G, on note [A,B] le sous-groupe engendré par le commutateur de la forme [x,y] pour x dans A et y dans B.

On définit alors par récurrence une suite de sous-groupes de G, notés Cn(G), par

  • C1(G) = G
  • Cn + 1(G) = [G,Cn(G)].

On dit que G est nilpotent s'il existe un entier n tel que Cn(G) = {e}. En outre, si G est un groupe nilpotent, sa classe de nilpotence est le plus petit entier n tel que Cn + 1(G) = {e}.

Exemples

  • Tout groupe abélien est nilpotent de classe 1.
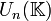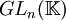  • Le sous-groupe U_n(\mathbb K) de GL_n(\mathbb K) formé des matrices triangulaires supérieures avec des 1 sur la diagonale est nilpotent de classe n − 1.

Propriétés

  • Un sous-groupe d'un groupe nilpotent est nilpotent. L'image d'un groupe nilpotent par un morphisme de groupe est un groupe nilpotent.
  • Soit Z(G) le centre de G. Si G n'est pas le groupe trivial, alors Z(G) n'est pas non plus trivial.
  • Si G/Z(G) est nilpotent, alors G est nilpotent.
  • Si H est un sous-groupe propre de G nilpotent, alors H est strictement inclus dans son normalisateur.

Groupe linéaires nilpotents

On a déjà vu que 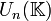U_n(\mathbb K) est un groupe nilpotent. Il possède la propriété intéressante d'être formé d'éléments unipotents, c'est-à-dire de la forme In + N, où N est une matrice nilpotente. Des théorèmes liés à la réduction des endomorphismes et aux représentations des groupes permettent de montrer la réciproque. Ceci peut être vu comme un analogue du théorème d'Engel sur les algèbres de Lie.

Soyons plus précis. On montre tout d'abord que si 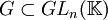G\subset GL_n(\mathbb K) est un sous-groupe formé uniquement d'éléments unipotents, alors tous les éléments de G sont simultanément trigonalisables. Autrement dit, on obtient que G est conjugué à un sous-groupe de 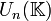U_n(\mathbb K). En particulier, G est nilpotent.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe nilpotent ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe Nilpotent de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Groupe nilpotent —  Ne doit pas être confondu avec Élément nilpotent. En théorie des groupes, les groupes nilpotents forment une certaine classe de groupes contenue dans celle des groupes résolubles et contenant celle des groupes abéliens. Les groupes… …   Wikipédia en Français

  • Groupe De Heisenberg — En géométrie différentielle, le groupe de Heisenberg, nommée en faveur de Werner Heisenberg, est le groupe de Lie réel de dimension 3, sous groupe de GL3(R) des matrices de la forme : Il est usuellement noté H3(R). Structure de groupe H3(R)… …   Wikipédia en Français

  • Groupe de heisenberg — En géométrie différentielle, le groupe de Heisenberg, nommée en faveur de Werner Heisenberg, est le groupe de Lie réel de dimension 3, sous groupe de GL3(R) des matrices de la forme : Il est usuellement noté H3(R). Structure de groupe H3(R)… …   Wikipédia en Français

  • Groupe De Frobenius — En mathématiques, un groupe de Frobenius est un groupe de permutation transitif sur un ensemble fini, tel qu aucun élément non trivial ne fixe plus d un point et tel qu un certain élément fixe un point. Ils ont été nommés en l honneur de F. G.… …   Wikipédia en Français

  • Groupe de frobenius — En mathématiques, un groupe de Frobenius est un groupe de permutation transitif sur un ensemble fini, tel qu aucun élément non trivial ne fixe plus d un point et tel qu un certain élément fixe un point. Ils ont été nommés en l honneur de F. G.… …   Wikipédia en Français

  • Groupe de Heisenberg — En géométrie différentielle, le groupe de Heisenberg, nommé en l honneur de Werner Heisenberg, est le groupe de Lie réel de dimension 3, sous groupe de GL3(R) des matrices de la forme : Il est usuellement noté H3(R). Structure de groupe… …   Wikipédia en Français

  • Nilpotent —  Ne doit pas être confondu avec Groupe nilpotent. En mathématiques, un élément x d un anneau unitaire (ou même d un pseudo anneau) R est appelé nilpotent s il existe un certain nombre entier positif n tel que . Sommaire …   Wikipédia en Français

  • Groupe de Frobenius — En mathématiques, un groupe de Frobenius est un groupe de permutation agissant transitivement sur un ensemble fini, tel qu aucun élément non trivial ne fixe plus d un point et tel qu au moins un point est fixé par un élément non trivial. Vu la… …   Wikipédia en Français

  • Groupe De Lie — En mathématiques, un groupe de Lie est un groupe qui est continu, c est à dire que chaque élément du groupe peut être approché d aussi près que l on veut par une suite d autres éléments du groupe. Un groupe de Lie est en fait un peu plus qu un… …   Wikipédia en Français

  • Groupe de lie — En mathématiques, un groupe de Lie est un groupe qui est continu, c est à dire que chaque élément du groupe peut être approché d aussi près que l on veut par une suite d autres éléments du groupe. Un groupe de Lie est en fait un peu plus qu un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”