Variable régionalisée

La VR comme phénomène physique : topographie de la ville de Binche.

La VR comme modèle mathématique : les courbes de niveau correspondantes

Utilisé essentiellement dans le domaine de la géostatistique, le terme de variable régionalisée (en abrégé : VR) désigne toute fonction mathématique déterministe^[1] destinée à modéliser un phénomène présentant une structure plus ou moins prononcée dans l'espace et/ou le temps^[2]. Par extension, et lorsqu'il n'y a pas de confusion à redouter, ce terme peut désigner le phénomène lui-même. Dans la première acception, une VR est donc un objet mathématique, susceptible à ce titre de manipulations théoriques ; dans la seconde, c'est un phénomène ou un événement physique, à la fois mesurable et existant indépendamment de l'observateur^{[Voir 1]} : cette dualité est suggérée par les deux images ci-contre, représentant un même territoire selon les deux points de vue.

La mise en œuvre des VR se justifie principalement pour rendre compte de phénomènes tout à la fois structurés et très irréguliers : tels sont par exemple le plus souvent les phénomènes naturels (minéralogiques, géophysiques, météorologiques, environnementaux, etc.), dont les comportements d'ensemble font apparaître une organisation globale dans l'espace et/ou le temps, mais dont la variabilité locale interdit toute modélisation par des expressions mathématiques simples. En revanche, même si rien n'interdit théoriquement de recourir au formalisme des VR de façon systématique, des informations totalement déstructurées pourraient plus avantageusement être traitées avec les outils des statistiques ; et à l'opposé, des phénomènes très réguliers pourraient être décrits par des fonctions simples ou des équations d'évolution.

Historiquement les premières utilisations du vocabulaire et du concept de « variable régionalisée » concernaient presque exclusivement la répartition des teneurs minéralisées dans un gisement minier ; mais cet outil a par la suite trouvé des applications dans des domaines aussi variés que la météorologie et la sylviculture^{[Voir 2]}, la bathymétrie et la topographie (MNT), l'environnement, l'agriculture de précision, l'halieutique, l'épidémiologie, le génie civil, toute cartographie quantitative en général, etc. Ainsi, sous un vocabulaire différent, une variable régionalisée est-elle strictement équivalente à la notion physique de champ, et plus précisément de champ déterministe^[1].

De plus, une variable régionalisée est fondamentalement une variable quantitative^[3] : elle attribue à tout point de l'espace une valeur numérique au sens large (i.e. éventuellement vectorielle ou complexe). Ainsi une variable régionalisée est-elle également un champ au sens mathématique : champ scalaire, ou vectoriel, ou tensoriel : à ce titre, elle est donc susceptible d'être étudiée par les outils de l'analyse, en particulier le calcul différentiel et le calcul intégral, ainsi que par les outils des statistiques.

Une VR n'a donc pas de domaine d'application spécifique, et elle n'est pas non plus un objet mathématique original. Mais l'adoption d'une nouvelle terminologie^{[Voir 3]} par les géostatisticiens, au début des années 1960^[4], a voulu prendre ses distances par rapport à un vocabulaire exclusivement mathématique ou exclusivement naturaliste, pour insister sur une des exigences premières d'une étude géostatistique^{[Voir 4]} : la recherche à chaque étape d'un équilibre constant entre les contraintes théoriques d'un modèle mathématique, et la nécessité de décrire au mieux et de traiter concrètement un phénomène réel^{[Voir 5]}. Ce qui signifie qu'il faut en permanence chercher à satisfaire à deux types d'exigences : en amont, la rigueur mathématique ; en aval, l'efficacité sur le terrain. En cours d'étude appliquée, le géostatisticien veille donc à ne jamais perdre de vue que, essentiellement, le concept de « variable régionalisée » opère à la charnière entre ces deux exigences : des exigences toujours complémentaires, mais parfois — voire souvent — contradictoires^{[Voir 6]}.


Cet article propose une simple mise en place de la notion de variable régionalisée, présentée dans l'esprit insufflé par le créateur de la géostatistique Georges Matheron et se fondant essentiellement sur ses publications. Les développements techniques et les propriétés mathématiques ne sont qu'abordés et renvoyés à la bibliographie, tandis que l'accent est mis sur la signification des concepts et la problématique de leur mise en œuvre.

Le premier paragraphe définit la variable régionalisée en tant qu'objet mathématique, et en évoque les propriétés et la signification. Le second paragraphe rappelle les caractéristiques physiques qui lui sont associées, et dont dépend le domaine de validité d'une étude géostatistique appliquée. Enfin, prenant acte des limitations de ce modèle jusque là déterministe, le troisième paragraphe met en place un cadre probabiliste, et décrit le mécanisme de va-et-vient entre une variable régionalisée et la fonction aléatoire qu'on lui associe : ce va-et-vient constitue le fondement de toute méthodologie de travail dans le cadre de la géostatistique intrinsèque.

Statuts mathématique et épistémologique

Propriétés théoriques

La définition complète d'une variable régionalisée, considérée abstraitement comme fonction d'un ensemble dans un autre, demande en toute rigueur de préciser la structure de l'ensemble de départ, la structure de l'ensemble d'arrivée, et les propriétés analytiques de la fonction. Mais en réalité, dans la plupart des cas, une VR sera simplement une fonction d'un espace métrique dans un autre.

Espace de départ

Dans la mesure où le premier objectif de la variable régionalisée est de rendre compte d'une structure spatiale, l'espace de travail — c'est-à -dire l'espace de départ de la fonction VR — doit pouvoir être muni, au moins localement[Voir 8], d'une fonction distance. Ainsi, dans la plupart des cas, l'objet mathématique « espace de départ » sera une représentation abstraite de la notion intuitive d'espace géographique. En général, cela ne présentera pas de difficulté particulière : il est ainsi facile de mesurer des distances dans un gisement, sur un terrain pollué, dans une forêt, ou de mesurer des intervalles de temps au cours du déroulement d'un certain processus. On peut cependant imaginer des situations plus complexes ; ainsi, une cartographie sur l'ensemble du globe terrestre (ou même seulement d'un hémisphère) se heurtera à des problématiques propres à la géométrie sphérique. On pourra éventuellement[11] dans ce cas traiter la sphère comme une variété[12] ; toutefois, la synthèse globale d'un ensemble de résultats locaux par ailleurs satisfaisants rencontrera immanquablement des difficultés théoriques probablement sévères ; un travail sur un réseau hydrographique (étude de paramètres physiques naturels, ou de teneurs en polluants, par exemple) aura très probablement à utiliser une distance ad hoc, l'espace de départ présentant ici la structure particulière d'un graphe simple. Éventuellement[11], la distance géodésique pourrait convenir  ; un travail relatif à l'évolution temporelle de cartes spatiales devra définir une distance spatiotemporelle qui fasse sens. Dans ce cas, la difficulté ne sera pas nécessairement de nature théorique, mais plutôt au niveau de la pertinence de l'outil mathématique ; en généralisant à des domaines plus abstraits, on pourrait imaginer de travailler par exemple dans un plan factoriel issu d'une analyse des données, et traiter un tel plan comme un territoire géographique : mais il faudra alors être très prudent dans la définition d'une distance sur un tel espace, et surtout dans la signification qu'on peut lui accorder. Toutefois, dans la pratique, l'espace de départ est le plus souvent simplement un espace euclidien. Il est en fait plus exact de parler d'un sous-ensemble d'un tel espace : en pratique en effet, on travaille toujours sur un domaine borné, dont la frontière[Voir 9] est fondamentalement tributaire des données disponibles et du problème posé[13]. Dans ces conditions, le plus simple et le plus courant est de considérer mathématiquement ce domaine de travail comme un sous-ensemble borné de , où n désigne la dimension (spatiale et/ou temporelle) de l'espace de travail. Alors que le domaine de travail et la dimension de l'espace sont imposés par la nature du problème à résoudre, le choix de la distance est en principe libre, dans les limites souvent larges imposées par les mathématiques. Cependant, dans la quasi-totalité des cas, on préfèrera naturellement si cela est possible[14] la distance euclidienne, d'une part parce que c'est elle qui permet les développements théoriques les plus simples[Voir 10], et d'autre part parce qu'elle correspond à la distance usuelle mesurée sur le terrain par les praticiens, du moins lorsqu'on ne doit utiliser que des coordonnées spatiales. En revanche, pour des études de nature spatio-temporelles, il n'est pas certain qu'une réponse purement mathématique soit satisfaisante : on pourra toujours en effet construire une distance mélangeant les coordonnées spatiales et temporelles, mais il est douteux que cette construction par ailleurs correcte théoriquement ait une signification concrète.	L'espace de départ doit être muni d'une métrique

Espace d'arrivée

Les objets de l'espace d'arrivée sont les valeurs prises par la VR en tout point de l'espace de départ.

Cas d'un champ scalaire

Si l'on travaille sur un champ scalaire[15], ces objets seront des nombres, la plupart du temps réels[16], de sorte que l'espace d'arrivée sera tout simplement . Dans ce cas d'une VR scalaire, la situation est simple à organiser : les valeurs prises par la VR sont des nombres qui s'expriment dans les unités de la variable étudiée. Ce seront par exemple des mètres (ou des pieds...) si la VR représente des altitudes topographiques, des mètres (ou des brasses...) si elle représente des profondeurs bathymétriques, des pourcentages (ou des g/T...) si elle représente une teneur de minerai, etc. Et comme l'objet de la géostatistique est essentiellement de caractériser les structures spatiales des objets étudiés, il faut pouvoir munir l'espace d'arrivée d'un outil théorique permettant de quantifier la ressemblance (ou la dissemblance) entre deux valeurs prises par la VR en deux points quelconques de l'espace de travail. De tels outils existent dans le cadre des statistiques usuelles ; le plus simple est la fonction d'autocorrélation, qui permet entre autres de quantifier la notion intuitive de « zone d'influence ». Cette fonction a pour arguments deux points quelconques de l'espace géographique, et leur associe un nombre sans dimension compris entre -1 et +1 qui représente le coefficient de corrélation entre les valeurs de la variable considérées en ces deux points. Ainsi en particulier, lorsqu'à deux points géographiquement distincts il correspond une valeur nulle de cette fonction, cela signifie qu'il n'y a pas de lien statistique mutuel entre les mesures effectuées en ces deux points, ou encore que la connaissance de la valeur prise par la VR en un point n'apporte (statistiquement) aucune information supplémentaire sur la valeur prise par la VR en l'autre point. Cette fonction est donc d'une grande importance d'abord pour comprendre et modéliser l'organisation spatiale de la variable d'intérêt, et ensuite pour la construction d'un estimateur, et plus particulièrement pour l'interpolation en cartographie ; et de fait, elle peut être utilisée en géostatistique, par exemple pour le krigeage simple. Toutefois, l'existence théorique de la fonction d'autocorrélation requiert des hypothèses fortes de stationnarité qui ne sont pas toujours satisfaites ; c'est pourquoi la géostatistique a dû très tôt[Voir 11] recourir à un autre outil. Dans un premier temps, cet outil est simplement l'écart quadratique entre les valeurs prises par la variable régionalisée en deux points de l'espace géographique. C'est une fonction de deux variables, de la forme générale : où symboliquement, et représentent respectivement, dans l'espace « géographique », les coordonnées des deux points concernés. Cette notation conventionnelle[17] ne préjuge en rien de la dimension ou de la nature de l'espace de départ : l'écriture peut aussi bien désigner une absisse sur la droite, un temps, une paire de coordonnées (abscisse, ordonnée) ou (module, azimut), etc. et sont les valeurs prises par la variable régionalisée aux points et . On rappelle qu'une VR est une fonction définie sur l'espace de départ, et cette fonction est ici notée .

Représentation d'une VR scalaire définie sur un domaine 2D

Si on suppose que cette surface représente une topographie, une fonction structurale possible sera le carré du dénivelé entre deux points ; elle définira la métrique de l'espace d'arrivée.

Dans ces conditions, la fonction apparaît comme une mesure du contraste existant entre les valeurs observées en deux points. C'est un premier outil de quantification de la structure (spatiale et/ou temporelle) de la variable régionalisée, une fonction structurale qui dépasse donc la simple information purement statistique puisqu'elle prend en compte non seulement les valeurs prises par la VR, mais également l'implantation des valeurs observées.

Toutefois, considérée comme dépendant de deux variables indépendantes et , cette fonction ne peut être un outil opératoire, pour au moins deux raisons :

• d'une part, elle constitue un objet mathématique encore plus complexe que la VR qu'elle entend représenter, ne serait-ce que parce qu'elle est cette fois fonction de deux variables au lieu d'une seule. Par ailleurs, les fluctuations numériques que l'on peut craindre pour cette fonction seront encore plus importantes que pour la VR elle-même, par l'effet de l'élévation au carré ;
• d'autre part, et de même que pour la VR elle-même, les valeurs prises par cette fonction ne seront expérimentalement accessibles que sur un nombre limité de (paires de) points expérimentaux, de sorte que l'objet mathématique ne sera connu que de façon extrêmement parcellaire, sans qu'il soit réellement possible de proposer une expression théorique acceptable. Plus exactement, il ne sera pas possible de faire un choix^{[Voir 12]}incontestable parmi les innombrables expressions théoriques différentes qui se révèleront compatibles avec le matériau expérimental disponible.

De la sorte, il est capital d'introduire des hypothèses de travail, autant que possible expérimentalement contrôlables, qui permettent de modéliser la fonction structurale en respectant deux contraintes antagonistes : rendre compte au mieux de la structuration de la VR, et constituer un objet aisément manipulable sur le plan mathématique. Cette démarche (partiellement évoquée ci-dessous), constitue l'essentiel de ce que les géostatisticiens appellent couramment variographie.

Cas d'un champ vectoriel ou multivariable

Le cas où l'ensemble d'arrivée est multidimensionnel met en lumière une problématique courante en géostatistique. Sur le plan mathématique en effet, cela ne change presque rien au cas scalaire : la VR demeure une fonction au sens strict ; ce n'est en aucun cas une fonction multiforme, ce qui signifie encore qu'à tout point de l'espace géographique, elle associe une et une seule valeur dans l'espace d'arrivée, quand bien même celle-ci serait un vecteur, un tenseur, ou plus généralement un multiplet de valeurs scalaires. Dans tous les cas, l'image par la VR d'un point quelconque de l'espace de départ est un élément unique (un singleton) de l'espace d'arrivée.

Un exemple trivial prouve du reste que la frontière théorique entre le cas scalaire et le cas multivariable est parfois très mince. Si l'espace d'arrivée est le plan complexe^[18], on peut aussi bien considérer la VR comme prenant des valeurs scalaires sur le corps des complexes , ou comme prenant ses valeurs dans un espace bidimensionnel sur le corps des réels ^{[Voir 13]}. Dans ces conditions, et toujours en en restant au niveau théorique, il est très facile de définir une métrique dans l'espace d'arrivée : on définira cette fois comme fonction structurale

où le symbole désigne le module du nombre complexe .

Par extension, si l'espace d'arrivée est un espace vectoriel, concrètement si les objets de l'espace d'arrivée sont des multiplets de valeurs qui s'expriment dans les mêmes unités, on pourra de façon naturelle adopter pour fonction structurale le carré du module. Par exemple, si la VR possède trois composantes , et ^[19], on posera

où le symbole désigne le module du vecteur .

En revanche, la formule précédente n'est plus utilisable si les différentes composantes qui constituent l'objet VR ne s'expriment pas dans les mêmes unités : la somme des carrés d'écart mélangerait des quantités hétérogènes, et n'aurait de ce fait plus aucune signification physique. Il faut donc définir une fonction structurale ad hoc, ce qui ouvre généralement la porte à un arbitraire^[20] inévitable^{[Voir 14]}. C'est une situation qui se présente presque inéluctablement lorsqu'on travaille dans un cadre multivariable : il n'y a en réalité aucune difficulté théorique nouvelle, et les développements mathématiques pourraient être poursuivis sans obstacles techniques ; mais la nécessité d'imposer au modèle de rendre compte dans de bonnes conditions de la réalité fait au contraire surgir des complication souvent considérables au niveau de la mise en œuvre et, dans ces conditions, l'expérience et le sens des responsabilités ont beaucoup plus d'importance que la rigueur mathématique^[21] pour mener à bien une étude appliquée.

Comme ces facteurs ne peuvent être inclus dans la matière d'un texte de présentation général, on n'évoquera plus par la suite que sommairement les spécificités du cas multivariable, bien que cela concerne en pratique la très grande majorité des études^[22]. Mais il ne faudra pas perdre de vue que dans la pratique, l'effort d'analyse critique et le dialogue constant avec le « client » occupent considérablement plus de temps du géostatisticien que la maîtrise des outils théoriques qui sont évoqués dans cet article, et que le choix d'une métrique pertinente sur l'espace d'arrivée constitue l'une des premières et des plus importantes étapes de ce travail critique.

Propriétés analytiques de l'application

Considérée comme une fonction (donc, un être mathématique), la variable régionalisée peut être un objet d'étude par tous les outils de l'analyse. On pourra donc s'interroger sur son comportement asymptotique, son analyse harmonique, les éventuelles EDP auxquelles elle satisfait, son Intégrabilité, etc. Naturellement, sauf dans le cas d'une recherche purement théorique, ce travail doit pouvoir être associé à des interprétations physiques, c'est pourquoi des modèles trop riches font courir un risque important de surinterprétation^[23] : on se trouve typiquement dans le cadre d'application du principe de parcimonie. Par ailleurs, même si le modèle et les hypothèses mathématiques sont corroborés par les observations de terrain, il faut garder à l'esprit que « la corrélation n'implique pas la causalité », autrement dit que la modélisation structurale ne prétend à aucune valeur explicative ; et plus précisément encore, la VR en tant qu'objet mathématique se limite à une description de la VR en tant que phénomène physique. Une éventuelle recherche d'interprétation, voire d'explication, relève de la seule responsabilité de l'utilisateur.

À cet égard, les caractères de différentiabilité de la VR constituent un exemple important, qu'il est utile de détailler. Pour éviter des difficultés techniques (utilisation de dérivées partielles ou directionnelles, problèmes stéréologiques), on se limitera au cas élémentaire où les espaces de départ et d'arrivée s'identifient à  : la VR est alors simplement une fonction réelle d'une variable réelle.

Une illustration essentielle : la notion de « régularité »

Pour une fonction réelle définie sur (ou sur un sous-ensemble préalablement précisé de ), le concept de « régularité » est parfaitement défini, et est associé au degré de dérivabilité de la fonction. De plus, le cas échéant, ce degré de régularité peut n'être vérifié que par morceaux. L'ensemble des fonctions qui satisfont à un critère de régularité donné possède la structure d'un espace vectoriel^[24], et les différents espaces vectoriels ainsi déterminés vérifient des relations d'inclusion strictes qui permettent de définir de façon rigoureuse une hiérarchie des caractères de régularité. Ainsi, en se limitant pour simplifier aux fonction définies sur tout entier,

• l'ensemble des fonctions continues par morceaux, noté , est l'ensemble des fonctions qui ne présentent qu'un nombre fini de discontinuités ;
• désigne l'ensemble des fonctions continues, c'est-à-dire ne présentant aucune discontinuité sur  ;
• désigne l'ensemble des fonctions dont la dérivée est continue par morceaux : intuitivement, il s'agit de fonctions qui ne présentent qu'un nombre fini de points anguleux ;
• désigne l'ensemble des fonctions dérivables ;
• désigne l'ensemble des fonctions indéfiniment dérivables, parfois qualifiées de « lisses » ou « régulières^[25] » ;

et l'on a la suite d'inclusions :

qui traduit une régularité (au sens mathématique) croissante.

Pour le géostatisticien appliqué, il est essentiel de pouvoir interpréter ces propriétés en termes physiques^[26]. La situation paraît simple lorsqu'il s'agit de continuité ou de continuité par morceaux : l'absence de discontinuité, ou la contrainte de n'avoir qu'un nombre fini de discontinuités, semblent être des propriétés effectivement observables sur le terrain, accessibles expérimentalement. Et pourtant, on est déjà en présence d'une forme discrète de « rupture épistémologique^[27] ». Car, contrairement à sa version mathématique, la continuité n'est en réalité pas clairement définie selon le sens commun. Pour illustrer cette affirmation, on peut penser à un exemple très simple de VR : la topographie. Dire que sur un territoire l'altitude est continue, cela signifierait qu'il n'y a nulle part de discontinuité, qu'il n'y a en aucun point de saut brutal d'altitude. Mais cette affirmation est-elle sensée si on observe des données séparées de quelques centimètre, a fortiori si on descend à des échelles microscopiques ? en fait, expérimentalement, le concept même de « continuité » garde-t-il un sens  ? voire, en allant jusqu'au paradoxe, peut-il exister une continuité à l'échelle atomique ? du reste, est-il encore pertinent de seulement parler d'« altitude » en deçà de certaines dimensions de l'observation ?

L'origine de ce hiatus est clairement identifiée : le concept mathématique de continuité, rigoureux, est une notion infinitésimale, et par ailleurs la VR est une « variable ponctuelle^[28] ». En revanche, la « continuité » selon le sens commun, et a fortiori la « régularité », sont des notions floues qui se fondent toujours (quoiqu'implicitement^[29]) sur une échelle d'observation et de travail. Or, ce facteur d'échelle est essentiellement absent du formalisme mathématique. Le rôle fondamental du géostatisticien (et de tout modélisateur) est alors de rapprocher les deux points de vue : préciser les notions trop floues du point de vue naturaliste, pour pouvoir les exprimer en des termes rigoureux ; et dans le même temps alléger autant que faire se peut les hypothèses mathématiques requises, pour leur permettre de décrire la réalité « dans de bonnes conditions » — étant entendu que le degré d'adéquation du modèle à la réalité est un paramètre ajustable, qui procède en général d'un dialogue entre le géostatisticien et son client.

À cet égard, l'ambivalence de l'expression « variable régionalisée » est ici dommageable. En effet (en gardant à l'esprit, à titre d'illustration, l'exemple de la topographie),

• on peut en général répondre sans ambiguïté à la question de savoir si la VR, en tant que fonction mathématique, est continue sur une domaine fixé ; et même si la réponse peut être difficile à obtenir effectivement^[30], la question est parfaitement formulée et ne requiert pas d'informations supplémentaires : un fonction est, ou n'est pas, continue. Il n'y a pas d'alternative ;
• au contraire, si la question de la continuité porte sur la VR en tant que phénomène physique, elle n'a pas de sens telle quelle, parce que la notion de continuité d'un phénomène nécessite d'être définie. Faute de quoi, on risque de ne pas savoir de quoi on parle ou, plus vraisemblablement encore, on risque inconsciemment d'invoquer des pseudo-définitions ajustées au coup-par-coup. Il convient en particulier d'accepter l'idée qu'une question en apparence aussi simple que la continuité appelle une réponse multiple, en fonction de l'échelle de travail : ainsi, la topographie d'un territoire fixé pourra sans doute être considérée comme (voire lisse^[31]) observée de l'espace, seulement ou à l'échelle kilométrique, discontinue à des échelles encore inférieures ; et sans doute sera-t-il purement et simplement impossible de la représenter par une fonction à l'échelle du caillou.

En cours d'étude, les caractéristiques structurales ne sont pas des attributs univoques de la VR physique, mais seulement des propriétés du modèle adopté hic et nunc ; mais rien n'interdit de proposer différents modèles pour un même phénomène. Alors que la réalité s'impose à nous, dans le même temps nous sommes seuls maîtres (bien sûr dans les limites du bon sens et de la rigueur mathématique) de nos choix intellectuels pour la modéliser. Un sujet de méditation^{[Voir 15]}...

Naturellement, ces difficultés méthodologiques sont accrues lorsque le concept mathématique concerné devient plus exigeant. Les remarques, peut-être inattendues, qui viennent d'être faites à propos de la VR (la topographie, dans l'exemple) deviendraient par exemple plus cruciales si on examinait la dérivée de la VR. Ainsi, une fonction mathématique est, ou n'est pas, dérivable sur un domaine ; mais quel sens donner à la « dérivée » — notion irrémédiablement infinitésimale — d'un phénomène physique, de surcroît la plupart du temps reconnu seulement sur un échantillonnage fini ? Quant au concept de « régularité », il est encore plus dangereux à manipuler, puisqu'en matière de fonction mathématique il signifie « infinie dérivabilité », alors qu'en dépit de son apparence intuitive il n'a tout simplement pas de définition univoque au niveau d'un phénomène physique : une rivière qui fait de nombreux méandres a-t-elle un tracé régulier comme l'affirmera un pêcheur depuis sa barque au milieu de l'eau, ou au contraire presque chaotique comme l'affirmera un cosmonaute la survolant à quelques centaines de kilomètres ?... Il n'y a pas de réponse universelle^{[Voir 16]}.

Exemples élémentaires

« Le modèle jamais n'est identique à la réalité. D'innombrables aspects du réel lui échappent toujours, et, inversement, le modèle contient toujours d'innombrables propositions parasites, sans contrepartie aucune dans la réalité^[32]. »

Or dans son sens mathématique de fonction, « la variable régionalisée n'est pas identique à la réalité, mais constitue déjà elle-même un modèle primaire^[33] ». Essentielle pour le déroulement ultérieur d'une étude géostatistique, la définition de ce premier modèle est certes en général peu problématique, mais elle permet de mettre en place de façon rigoureuse le cadre de travail théorique, et attire éventuellement l'attention sur les difficultés à venir. À titre d'illustration, les exemples suivants présentent quelques interrogations qui peuvent surgir dès cette première étape.

Topographie

Une première illustration déjà évoquée, très simple, peut être donnée par la topographie d'un certain territoire géographique D. En tout point de coordonnées (x,y)[34] de ce territoire, la valeur de l'altitude peut être considérée comme le résultat d'une application z0 du domaine géographique D dans l'ensemble des réels Même si cela paraît naturel, le fait même de représenter la topographie par une VR (donc : une fonction) implique une hypothèse : que le relief ne présente pas d'encorbellement. En l'occurrence, ce n'est pas une restriction très importante, mais cette remarque montre que l'étape de modélisation la plus anodine peut déjà comporter des présupposés. Dans la mesure où l'élaboration d'un modèle n'est pas un but en soi, mais constitue seulement la mise en place d'un outil destiné à répondre à des questions concrètes, il est bon de ne jamais perdre de vue cette propriété essentielle, afin que les développements théoriques ultérieurs ne s'éloignent pas subrepticement de la réalité. Dans ce cas précis, il y aurait une difficulté à tracer des courbes de niveau (par exemple pour une carte d'état-major) s'il existait des zones du domaine cartographié où la variable topographie peut présenter deux valeurs distinctes en un même point : une situation certes très rare, mais pas totalement impossible dans certains reliefs particuliers (certaines montagnes, falaises, canyons...). Si la topographie peut effectivement être modélisée par une VR, la propriété de continuité du modèle s'écrira : , puisque cette fois l'espace géographique est , sous-ensemble de .Cette propriété s'associe intuitivement à l'idée d'une carte dont les courbes de niveaux ne présentent aucune anomalie (aucune discontinuité, et aucune zone d'accumulation). Peut être de signification physique plus claire, la propriété de continuité par morceaux[35], qui s'écrira : , signifie qu'il n'existe qu'un nombre au plus fini de falaises verticales sur le domaine. Et de même, la différentiabilité par morceaux — — pourra être interprétée comme la présence d'un nombre au plus fini d'arêtes vives (ruptures de pente : crêtes ou sillons) sur le domaine. Mais naturellement, ces différentes caractéristiques intuitives (pas de discontinuités, pas de falaises, pas de rupture de pente — ou seulement en nombre fini) n'ont de sens pratique qu'associées à une certaine échelle d'observation, et ce facteur d'échelle est absent du formalisme mathématique : la VR « ne connaît pas[36] » les conditions dans lesquelles les valeurs numériques des données ont été acquises. C'est à l'utilisateur et à lui seul qu'il appartient d'intégrer ces informations complémentaires dans l'interprétation des résultats que produira un algorithme qui n'était pas en mesure de les prendre en compte.

Exemple déjà rencontré d'une surface topographique

Cette surface présente, comme objet mathématique, un grand caractère de régularité : elle est différentiable.

Météorologie

Sur le même territoire que précédemment, on peut aussi s'intéresser à des paramètres météorologiques mesurés à une distance fixée du sol. Un point du domaine étudié est donc cette fois repéré par trois coordonnées (par exemple, latitude, longitude et altitude), de sorte que l'espace de départ est à trois dimensions. Observons que l'altitude z, qui était la variable d'intérêt dans l'exemple précédent (donc, appartenait à l'espace d'arrivée), a cette fois le statut d'une coordonnée. Supposons alors que l'on s'intéresse en tout point aux valeurs respectives de la température (scalaire) et de la composante horizontale du vent (vecteur à deux dimensions). La VR (notée f pour la circonstance) sera donc une application :

Cet exemple appelle quelques remarques :

• concernant l'espace de départ, il n'est pas très judicieux de le considérer comme étant à trois dimensions. En effet, si la mesure est effectuée à une distance imposée du sol^[37], la donnée des deux coordonnées x et y implique la valeur de la troisième z. Bien sûr, il peut s'agir d'une relation très compliquée et de surcroît mal connue, et de fait c'est très exactement la VR z₀ présentée dans l'exemple précédent ; mais en réalité, la détermination d'un point de donnée est entièrement réalisée à l'aide de seulement deux paramètres indépendants x et y, quand bien même ce point de donnée est plongé dans un espace tridimensionnel. Ou encore, dit autrement, les coordonnées (x,y,z) sont bien au nombre de trois, mais elles sont globalement liées. Aussi, d'un point de vue mathématique, il sera plus correct de considérer l'ensemble de définition de la VR f comme une variété à deux dimensions. Mais en conséquence, la définition d'une distance sur cet ensemble de départ pourra se révéler problématique : la distance euclidienne sera sans doute encore admissible sur un domaine sans grand relief, mais deviendra totalement inadaptée sur un domaine au relief très contrasté ;
• naturellement, toujours en s'appuyant sur ce même domaine D, on pourrait aussi travailler avec des données véritablement tridimensionnelles, par exemple transmises par des ballons-sondes lancés depuis un point de D^[38]. En quelque sorte, par comparaison à l'exemple précédent, la troisième coordonnée z retrouverait sa liberté par rapport aux deux autres. Dans ces conditions, le travail sur un espace de départ 3D retrouve sa pertinence, et le domaine de départ D' est effectivement un domaine tri-dimensionnel, dont D n'est plus qu'un sous-ensemble. La donnée de la topographie pour devra plutôt être rapprochée de la notion de condition initiale, puisque toutes les valeurs des altitudes des points de mesure auront cette valeur de la topographie comme borne inférieure :

• la valeur prise en tout point par la variable régionalisée se présente ici comme un triplet de valeurs numériques. En l'occurrence, il est plus prudent d'utiliser cette expression neutre que de parler d'un vecteur à trois dimensions. En effet, les trois composantes de ce triplet sont de natures physiques différentes, et bien que l'opération soit possible mathématiquement, on imagine mal ce que pourrait être la signification d'une formule de changement de base, sachant que parmi ces trois composantes l'une s'exprime (par exemple) en degrés Celsius et les deux autres (par exemple) en m/s ; en revanche, une telle formule aurait un sens si on se limitait aux deux composantes de vitesse : c'est pourquoi, afin de garder le contact avec l'interprétation physique, il est instructif de désigner l'espace d'arrivée comme étant plutôt que .

À l'occasion de cet exemple météorologique, on peut évoquer une autre problématique. Supposons que la première composante du domaine d'arrivée mesure la hauteur géopotentielle pour une valeur de la pression atmosphérique, et que le domaine horizontal d'étude soit situé dans une zone géographique qui autorise l'approximation géostrophique^[39]. Le domaine de définition de cette nouvelle VR f est donc de la forme ^[40]. Les trois composantes de f^[41]  :

sont, en vertu de cette approximation, reliées (à p fixé) par un système d'EDP :

où λ est une constante (à p fixé) si le domaine n'est pas trop étendu.

Ainsi, mathématiquement, le vent géostrophique est caractérisé par le géopotentiel, ou encore : les deux dernières composantes de la VR sont caractérisées par la première. Il ne s'agit ici que d'une simplification, mais cet exemple illustre qu'il peut exister non seulement des liens statistiques, mais même des liens fonctionnels entre les composantes d'une VR. C'est ici l'occasion de souligner une nouvelle fois la différence entre les points de vue mathématique et physique.

En effet, on pourrait croire que l'approximation géostrophique peut dispenser de réaliser des mesures de vent. On pourrait aussi penser que ces équations permettent, avec les seules mesures du vent, de vérifier l'hypothèse géostrophique puisqu'on doit avoir en vertu du théorème de Schwarz :

.

Pourtant, en pratique, il n'en est rien. Les données étant nécessairement en nombre fini, il n'est strictement pas possible de mesurer les composantes du vent en dérivant dans les deux directions principales les valeurs du géopotentiel, pas plus qu'il n'est possible de mesurer les dérivées partielles des composantes du vent — une nouvelle fois parce que la dérivation est une opération essentiellement infinitésimale, qui est fondamentalement irréalisable avec un jeu fini de valeurs.

Tout au plus pourra-t-on proposer des algorithmes d'estimation, par exemple du vent à partir du géopotentiel, en utilisant les équations théoriques fournies par la physique. On pourra aussi réaliser d'autres manipulations fondées sur les trois composantes de la VR f et tenant compte de l'équation théorique reliant ces trois composantes : cette approche est un des fondements de la géostatistique multivariable (cf. bibliographie : H. Wackernagel, 2003). Mais quelqu'intéressants puissent être les résultats ainsi obtenus, il est capital de garder à l'esprit qu'il s'agit d'artefacts^[42], de produits issus d'un algorithme, et non pas de données brutes. Ce sont des images de la réalité, non des mesures de la réalité^[43].

Pollution

Imaginons à titre de dernier exemple que le phénomène à étudier soit la pollution d'une rivière par un certain polluant p. Compte-tenu de la variable étudiée, il semble judicieux de ne pas utiliser la distance euclidienne^[44], surtout si la rivière effectue de nombreux méandres : il est bien préférable de compter les distances en suivant le cours de la rivière, puisque c'est le parcours que suit le polluant. Pour simplifier l'exemple, on ne tiendra pas compte des variations de pollution dans la largeur de la rivière, et on supposera que le tronçon étudié ne comporte pas d'affluents : dans ces conditions, il est naturel de repérer spatialement une mesure uniquement pas son abscisse curviligne s soit encore, plus concrètement, par la distance à un point de référence^[45] en suivant le tracé de la rivière. Dans ces conditions, et en supposant que la mesure de pollution est un scalaire, la VR est une simple application de dans  :

Les méandres de la Seine entre Vernon et Le Havre		Il n'y a pas de difficulté en ce qui concerne le repérage géographique, et l'espace de départ peut effectivement être muni d'une métrique. Toutefois, la nature de la variable étudiée ne peut se contenter d'une seule information de distance ; lorsqu'on compare deux points, la mesure de l'écart qui les sépare est une information assez pauvre : en particulier, il n'est pas indifférent de savoir lequel des deux points est en amont et lequel est en aval. Cette information ne peut être prise en compte par une distance, qui est par nature une fonction symétrique des deux points auxquels elle s'applique. Anticipant sur les méthodes de la géostatistique multivariable, on peut suggérer de rajouter l'abscisse curviligne s comme variable supplémentaire, et envisager d'étudier conjointement les variables s et p(s) avec les outils appropriés pour un travail multidimensionnel : par exemple, étudier le nuage de corrélation entre et [46] pour essayer de mettre en évidence une dérive (tendance). De plus, il est très probable que la structure locale de la pollution dépend aussi de la vitesse du courant : on peut donc égqlement rajouter cette donnée ou plutôt, ce qui sera sans doute plus simple, l'altitude z(s) qui constituera vraisemblablement une bonne variable explicative. Dans ces conditions, la VR apparaîtra comme une application : On peut aussi du reste, si les données le permettent[47], choisir un autre angle d'attaque et faire intervenir le facteur temps et la vitesse de propagation du polluant le long de la rivière, donc le débit... Cette réflexion sommaire souligne l'intérêt qu'il peut y avoir à solliciter des variables auxiliaires qui, sans présenter de réel intérêt en elles-mêmes, peuvent aider à affiner la connaissance structurale de la variable d'intérêt tout en permettant de continuer à bénéficier des outils généraux de la géostatistique. Naturellement, l'ajout de nouvelles variables introduit la problématique, déjà rencontrée, du choix d'une métrique dans l'espace d'arrivée... De nouveau, la responsabilité du géostatisticien est décisive pour la pertinence et l'efficacité des développements du modèle.
Il n'est pas approprié ici d'utiliser la distance euclidienne (à vol d'oiseau) entre les points de mesures, si la variable étudiée est tributaire du courant du fleuve.

Signification d'une VR : approche critique

Les commentaires qui ont jusqu'ici jalonné la mise en place du concept de VR, ainsi que les quelques exemples élémentaires proposés, constituent une illustration de l'aphorisme d'Alfred Korzybski : « une carte n'est pas le territoire^[48] ». La « rupture épistémologique » est bel et bien déjà à l'œuvre, et il convient de la garder à l'esprit si, comme c'est fréquent, on utilise le vocabulaire variable régionalisée pour désigner aussi bien le phénomène que la fonction mathématique qui le modélise : la VR-fonction n'est pas la VR-phénomène.

À l'examen, cette mise en garde apparaît en fait comme de simple bon sens. Pour en revenir au vent géostrophique par exemple, les équations expriment que le vecteur V (objet mathématique) est le gradient (opération mathématique)^[49] de la hauteur géopotentielle h (objet mathématique) dans le cadre de l'hypothèse d'équilibre géostrophique. Mais quel sens cela aurait-il de déclarer : « l'équilibre géostrophique, c'est lorsque le vent (phénomène physique)^[50] est le gradient (notion physique non définie^{[Voir 17]}) de la hauteur géopotentielle (donnée physique)^[51] » ? La formulation correcte, qui rendrait compte rigoureusement de la relation entre phénomène et modèle, serait : « nous dirons (par définition) qu'il y a équilibre géostrophique lorsque le vecteur adopté^[52] pour modéliser le vent peut être considéré^[52] comme le gradient de la fonction adoptée^[52] pour modéliser la hauteur géopotentielle  ». Et incidemment, cette formulation a aussi pour mérite de souligner que l'« équilibre géostrophique » est une propriété du modèle, et non un phénomène physique observable et indépendant de l'observateur^[53] ; de fait, cette formulation constitue très exactement une définition, rigoureusement exprimée, du concept mathématique d'« équilibre géostrophique ».

Naturellement, un tel énoncé aussi puriste est très lourd, et ne se trouve jamais dans les publications ; les risques d'accidents méthodologiques demeurent en effet assez limités. De sorte que par exemple, dans l'usage géostatistique, l'expression variable régionalisée est selon le contexte utilisée dans l'une ou l'autre de ses acceptions.

Mais pour parer d'éventuels faux-sens^[54], le lecteur se doit de garder en mémoire la sentence de Korzybski. C'est du reste l'occasion de noter que cet aphorisme soulève implicitement trois points importants :

Carte et territoire : au-delà du jugement de valeur

Certes, la carte n'est pas le territoire, mais cette distinction ne doit pas inciter à opérer une classification, un jugement de valeur, une hiérarchie. Il serait erroné^[55] de vouloir affirmer une quelconque « supériorité » de la carte sur le territoire (ou l'inverse). Scientifiquement, cela n'a pas de sens d'exprimer une « préférence » entre réalité et modèle : ces deux objets sont de natures essentiellement différentes, et à ce titre ne sauraient être classés. Leurs statuts épistémologiques sont différents, leurs rôles dans le déroulement d'une étude sont différents : la réalité existe indépendamment de nos choix personnels, et s'impose à nous ; le modèle est notre création, et nous devons le dominer^[56].

Mais dans le même temps, dès qu'on se consacre à de la géostatistique appliquée, l'élaboration d'un modèle n'est pas une fin en soi, et a vocation à rendre compte du réel. C'est pourquoi il est important d'associer à chaque modèle un critère permettant d'apprécier, si possible de façon quantitative, l'adéquation de ce modèle à la réalité. Et cette notion d'adéquation, qui doit être définie a priori, est clairement contingente et tributaire du problème à résoudre : toute choses égales par ailleurs (domaine étudié, données disponibles, contraintes de calcul, etc.), une modélisation donnée n'aura pas la même pertinence selon la question posée^{[Voir 15]} : ainsi serait-il tout-à-fait illusoire d'espérer atteindre un outil universel d'évaluation des modèles. Au contraire, un critère est nécessairement conventionnel, et sa caractérisation s'apparente étroitement au choix déjà rencontré lors de la définition d'une métrique : choix qui comporte donc une part importante et inévitable d'arbitraire — ce mot une nouvelle fois n'ayant aucune connotation négative. Il existe donc en théorie une grande liberté dans les choix de critères, même si des raisons très diverses (culturelles, considérations de facilité de mise en œuvre, voire mode du moment en cours dans le milieu scientifique...) peuvent limiter ces choix ; il est par ailleurs prudent de s'en tenir au principe de parcimonie.

Il est important à ce propos de noter que la VR (fonction) n'obéit pas en général^[57]à ce principe. En effet, ayant vocation en tout point x à prendre une valeur z(x) qui serait exactement ce que l'on pourrait mesurer sur le terrain^[58], la VR est d'une incroyable complexité, et ne pourra être explicitée par une expression mathématique simple et utilisable. On pourra certes considérer que la VR-fonction décrit de façon optimale voire parfaite^[59] la VR-phénomène, mais cette perfection est stérile, parce que non opératoire : on est condamné à des manipulations purement tautologiques. Ainsi, de façon essentielle, le modèle primaire se révèle-t-il la plupart du temps inopérant en tant que tel^{[Voir 18]}, et c'est pourquoi la géostatistique s'est orientée vers des modèles plus élaborés, de nature probabiliste (voir paragraphe 3 du présent article). Ainsi, pour revenir à l'aphorisme de Korzybski, on peut l'enrichir en insistant : « aucune carte n'est le territoire » et de surcroît, la seule qui pourrait prétendre rendre compte du réel, exactement et point à point, est en fait en général irréalisable.

Cela dit, pour tout traitement numérique d'un phénomène donné, la variable régionalisée constitue l'information quantitative irréductible la plus fondamentale, le socle sur lequel peuvent être élaborés tous les modèles ultérieurs, la référence ultime à laquelle il faut revenir en cas de difficulté méthodologique^[60]. Ce rôle basique a conduit Matheron à introduire la très importante notion de grandeur régionale : « Nous appelons grandeur régionale, ou simplement régionale, toute fonctionnelle de la variable régionalisée z(x) définie sur S, c'est-à-dire toute grandeur dont la valeur se trouve déterminée par la donnée de toutes les valeurs numériques z(x) lorsque x parcourt S^[61]. » Par conséquent, pour éviter tout risque de hiatus entre les développements théoriques^[62] et le problème réel qu'ils sont censés résoudre, il faut veiller à ce que les énoncés des résultats puissent se formuler en termes de grandeurs régionales afin de laisser, au moins en théorie, une possibilité de contrôle a posteriori.

Encore faut-il être bien conscient que ces contraintes méthodologiques sont virtuelles, et ne sauraient être actuelles si le domaine de travail est un continuum, puisqu'il n'est pas possible de réaliser une infinité non dénombrable de mesures. Tout au plus peut-on (imaginer) réaliser les mesures sur un ensemble fini de points quelconques désignés dans l'espace. La difficulté ici n'est pas conceptuelle, mais seulement technique, et s'apparente à une problématique classique rencontrée par exemple en échantillonnage ; ainsi une grandeur régionale, si elle ne se limite pas à une combinaison finie de valeurs ponctuelles de la VR, ne pourra-t-elle jamais être mesurée au sens strict, mais on pourra toujours en proposer une approximation : cela ne sera qu'une question de collecte de l'information.

Comparaison de différents modèles

Une fois qu'il a été convenu d'un critère d'évaluation, rien n'interdit de comparer entre eux différents modèles afin d'exprimer des préférences. Il peut s'agir d'une simple dichotomie : modèles acceptables vs. modèles à rejeter. Mais s'il s'agit d'un critère numérique, on peut aller plus loin et classer les modèles testés : on considérera en général^[63] qu'un modèle est d'autant meilleur que sa distance à la VR est plus faible. Ainsi, alors qu'il était dépourvu de signification d'établir un jugement de valeur comparée entre modèle et réalité, il est au contraire possible — et souhaitable — de chercher à établir une hiérarchie entre modèles. Mais cette hiérarchie est bien sûr fondamentalement tributaire du critère adopté, donc comporte une part importante d'arbitraire.

Par exemple, si l'on prend comme critère une fonction de la seule distance du modèle à la VR, le meilleur modèle possible sera par construction la VR (fonction) elle-même ; mais cette réponse ne sera évidemment pas satisfaisante, puisque c'est un objet mathématique impossible à expliciter et à manipuler. À l'opposé, rien n'interdit par exemple de modéliser l'ensemble d'un phénomène^[64] sur un certain domaine par la moyenne arithmétique des données de la VR mesurées sur ce domaine : on peut difficilement imaginer plus simple, mais on perd toute l'information structurale sur le phénomène en résumant toute sa complexité par un seul nombre...

Deux points de vue à la fois opposés et complémentaires se rencontrent dans cette recherche d'un critère de qualité, selon la priorité que l'on se donne :

• on peut vouloir privilégier les propriétés intrinsèques du modèle. Par exemple, si le but est d'avoir une vision globale et lissée du phénomène, on préférera un modèle présentant de bonnes caractéristiques de régularité^[65]. Si on souhaite modéliser un profil d'aile d'avion ou de carrosserie automobile, on cherchera un modèle qui optimise l'aérodynamisme, ou la portance. On peut appeler ce type de contraintes des « contraintes aval », puisqu'elles concernent des propriétés futures de ce que l'on va construire. Ce point de vue est par exemple celui de la modélisation par fonctions splines ;
• on peut vouloir privilégier la fidélité du modèle à la réalité ; c'est, en général, le choix de la géostatistique. Encore cette contrainte de « fidélité » doit-elle être définie : selon le cas, le but sera d'avoir un modèle précis (dans un sens à son tour à définir), et tel est le point de vue du krigeage ; et dans d'autres cas, on insistera plutôt sur le respect des textures, on souhaitera que le modèle « ressemble » à la réalité^[66], et tels seront les points de vue des MNT ou, en géostatistique, des simulations conditionnelles ou non^[67]. On pourra parler ici de « contraintes amont ».

Une nouvelle fois, il n'existe pas de choix « vrai » ou « faux » quand il s'agit d'opter entre contraintes amont et contraintes aval. Il y a des choix judicieux ou non, efficaces ou non, en fonction des questions que l'on souhaite résoudre, des moyens dont on dispose, des contraintes économiques, etc. Et la rigueur méthodologique exige de ne pas réajuster, de façon ad hoc et a posteriori, un critère de qualité en fonction de la conclusion que l'on souhaite promouvoir.

Domaine de validité du modèle

Toujours pour rester dans la terminologie de Korzybski, la question est enfin de savoir ce que devient la carte au-delà du territoire. En d'autres termes, cela pose le problème de l'extrapolation. En effet, le territoire étudié (physiquement) est nécessairement borné alors que les modèles (mathématiques) utilisés ont bien souvent un domaine de validité illimité. Or, sans même aller jusqu'à parler de comportements asymptotiques, quelle signification pourra-t-on alors attribuer à un énoncé du modèle relatif à des portions de l'espace éloignées des données disponibles ? Ou encore : quelle confiance peut-on accorder à « ce que nous dira » un modèle en-dehors du domaine sur lequel il a été ajusté ? La question n'est pas académique : par exemple, les prévisions météorologiques ou économiques sont essentiellement intéressantes pour le futur, c'est-à-dire pour un intervalle de temps où par nature on ne dispose d'aucune information permettant de corroborer ou d'infirmer le modèle...

Cela est inéluctable : lorsqu'on sollicite le modèle sur des domaines d'espace ou de temps où il n'a pu être contrôlé, ou lorsqu'on en invoque des propriétés mathématiques qui n'ont pu être associées à des particularités physiques, on court inévitablement le risque que les développements théoriques, désormais privés du contrôle des données mesurées sur le terrain, proposent des résultats dépourvus de toute vraisemblance, voire absurdes^[68] . La raison de ce danger est facile à comprendre : l'adoption d'un modèle, en effet, constitue toujours une hypothèse anticipatrice^[69] puisque, selon une citation déjà rencontrée^[32], « ...le modèle contient toujours d'innombrables propositions parasites, sans contrepartie aucune dans la réalité. ». Le paradoxe apparent tient à ce que l'introduction d'une telle hypothèse anticipatrice, bien que source de dangers et d'incertitudes, est dans le même temps indispensable : c'est elle qui permet de sortir des manipulations tautologiques sur des amoncellements de valeurs numériques, et de produire des résultats intelligibles et opératoires.

En résumé, deux risques de dépassement du « seuil de réalisme », deux types d'extrapolations se présentent :

• appliquer sans discernement le modèle, par ailleurs correctement corroboré par les informations expérimentales disponibles, en dehors du domaine (physique) géographique ou temporel sur lequel il a été ajusté. On peut parler à ce propos d'extrapolation physique ;
• solliciter des caractéristiques du modèle autres que celles qui en ont guidé l'inférence. On peut alors parler d'extrapolation méthodologique ou intellectuelle.

Ces deux types d'extrapolation ne sont pas condamnables en eux-mêmes, et sont même parfois indispensables. Mais ils aggravent le risque que les développements méthodologiques et leurs conclusions s'éloignent de façon inacceptable de la réalité, le risque de commettre une erreur radicale^[69]. Un risque inévitable, souvent fécond, et inhérent à toute démarche de représentation théorique du réel ; il appartient au praticien d'utiliser au mieux son sens critique et son expérience pour minimiser ce risque, sous sa responsabilité.

Une illustration sur un cas simple

Profil bleu : variable régionalisée, l'image numérique la plus fidèle de la réalité ; Points jaune  : huit données, seule information quantitative effectivement accessible.

Afin d'illustrer la démarche critique exposée précédemment, on propose ici un exemple simplifié, à une dimension, construit pour la circonstance. On pourra penser par exemple à un profil topographique décrivant un relief en bordure de mer (les valeurs d'altitudes sont négatives sur un des bords du domaine : on pourrait les interpréter comme des profondeurs bathymétriques). Pour fixer les idées, on pourra supposer que les unités sur les deux axes sont des hectomètres. Il s'agit d'une construction académique, puisque la totalité de la variable régionalisée a ici été construite par un algorithme mathématique, donc pourrait être effectivement connue. Elle est représentée ci-contre par le profil bleu clair. Cette situation est, en toute rigueur, complètement irréaliste lorsqu'on travaille sur des mesures physiques expérimentales, puisqu'il n'est pas envisageable d'accéder à la connaissance effective d'un continuum de valeurs strictement ponctuelles. Toutefois, avec une approximation que l'on peut juger acceptable[70], cette connaissance exhaustive de la VR pourrait être considérée comme atteinte dans certains cas particuliers, en télédétection par exemple : on peut ainsi éventuellement admettre qu'une image satellitale apporte une information exhaustive[71] d'un phénomène physique. Cependant, dans la très grande majorité des cas, la réalité n'est mesurée numériquement que par un nombre fini de données ponctuelles, de surcroît en général réduit. Cet état de fait soulève le problème très important de l'échantillonnage, et en particulier la question de la représentativité des échantillons[72] : la valeur d'un jeu de données ne dépend pas seulement de la quantité de l'information disponible, mais aussi de sa qualité, c'est-à-dire en particulier de l'organisation géographique de son implantation. Dans l'exemple examiné ici, on suppose que l'on ne dispose que de huit données irrégulièrement réparties, représentées par des points jaunes. Ainsi, si l'on s'en tient aux seules données numériques, les huit valeurs d'altitudes (et les huit coordonnées correspondantes) associées à ces huit points constituent la seule information disponible.

Méthodologiquement, la mise en œuvre de cet exemple académique s'impose d'elle-même : on se place dans l'environnement d'une étude réelle, c'est-à-dire qu'on ne s'autorise donc à utiliser que les huit mesures ponctuelles désignées ; mais on pourra a posteriori comparer les constructions effectuées et la réalité de la courbe bleue. Cette situation extrêmement privilégiée n'est évidemment pas envisageable dans la réalité, où la VR n'est accessible en pratique que sur un jeu fini de mesures. Sur le terrain, le seul contrôle éventuellement possible^[73] consiste à aller effectuer des mesures supplémentaires en des points où initialement l'on ne disposait pas de données, et à en comparer la valeur à ce que proposent les algorithmes développés sur la base des données initiales.

Carte et territoire : au-delà du jugement de valeur

Le panneau ci-dessous n'a pour but que de rendre sensible la différence fondamentale de nature séparant la « carte » et le « territoire », et d'illustrer la sentence déjà évoquée : « Le modèle jamais n'est identique à la réalité. D'innombrables aspects du réel lui échappent toujours, et, inversement, le modèle contient toujours d'innombrables propositions parasites, sans contrepartie aucune dans la réalité^[32]. »

Esterel, bord de mer Hawke's Bay, Nouvelle-Zélande Watch Hill, Rhode Island Foz do rio Sado Profil bleu : variable régionalisée, l'image numérique la plus fidèle de la réalité ; Points jaune  : huit données, seule information quantitative effectivement accessible ; île Marion, Afrique du Sud Baie Erebus, Antarctique Èze, Alpes Maritimes

Les différents paysages proposés sont tous, au prix éventuel d'un changement de coordonnées, compatibles avec le profil de la VR, et a fortiori avec les huit données disponibles. Leur variété met en lumière tout ce que l'étape de modélisation fait perdre au niveau de la connaissance brute d'un phénomène, et ceci dès le niveau du modèle primaire. Mais inversement, la fonction mathématique VR autorise des constructions intellectuelles qui permettront de dépasser la simple accumulation de données numériques, et de proposer des synthèses aidant à enrichir cette phase de connaissance brute et à proposer des schémas de compréhension du phénomène. Ainsi phénomène et modèle ont-ils des rôles essentiellement complémentaires, et la tâche du géostatisticien est de veiller à assurer cette complémentarité tout au long d'une étude.

Toutefois, dans le cadre d'une étude appliquée, il va de soi qu'en cas de désaccord entre les développements du modèle et les observations^[74] de contrôle a posteriori, c'est le modèle qu'il faut corriger : le modèle a vocation à représenter le réel, tandis que celui-ci n'a pas à se plier à nos représentations intellectuelles. C'est cette dissymétrie qui fait toute l'efficacité de la démarche scientifique^[75], et c'est la maîtrise opératoire de cette dissymétrie qui caractérise la valeur d'un praticien.

Comparaison de différents modèles

En plus du profil de la VR et des huit points de données, l'animation ci-contre affiche six modèles possibles pour représenter le phénomène. Il a été choisi ici de ne proposer que des modèles qui respectent les données, c'est-à-dire qui restituent exactement la valeur des données aux points où des mesures ont été effectuées : ainsi, la VR comme les six modèles passent exactement par les huit points de données. Cette contrainte paraît de bon sens, mais elle n'est pourtant nullement obligatoire : on pourrait par exemple imaginer que les mesures sont entachées d'erreur, et que par conséquent il n'est pas judicieux de chercher à toute force à restituer avec le modèle la valeur affichée par l'appareil de mesure. Du reste, les appareils de mesures sont usuellement accompagnés de spécifications techniques qui fournissent, en particulier, leur degré de précision, et cette information capitale est un élément important pour guider l'utilisateur dans la définition d'un critère de qualité pour ses modèles. Il semble dès lors intuitif que, si l'on choisit de respecter les données, les différentes représentations possibles de la réalité se ressembleront d'autant plus qu'il y aura beaucoup de données, puisque toutes ces courbes seront astreintes à passer par les mêmes points : il s'agit d'un effet traditionnellement appelé conditionnement en géostatistique, et le conditionnement par les données constitue en quelque sorte une force de rappel qui contraint les modèles à ne pas trop s'éloigner de la réalité. Cette intuition doit cependant être considérée avec précaution ; imaginons que la VR de cet exemple ait été reconnue par 201 points : sa modélisation par un polynôme de degré 200[76] aurait été d'une énorme instabilité numérique en fonction des coordonnées de ces points, bien loin de l'allure générale de la VR en dépit d'un conditionnement très fort. Quant à ce qui concerne le conditionnement par huit points, il est au contraire très lâche, et on peut a priori s'attendre à des modélisations non seulement différentes quant à leurs textures (caractéristiques morphologiques de détail), mais même en ce qui concerne leurs allures générales.

Profil bleu : variable régionalisée, l'image numérique la plus fidèle de la réalité ; Points jaune  : huit données, seule information quantitative effectivement accessible ; Profils rouges : exemple de fonctions numériques, dérivables ou indéfiniment dérivables, censées représenter la réalité en compatibilité avec l'information disponible.

On peut attendre d'un modèle, censé rendre compte de la réalité, au moins trois types de propriétés :

1. « être beau » (concrètement : obéir à des conditions de régularité posées a priori), ce qui a été précédemment qualifié de « contrainte aval » ;
2. être précis (dans un sens qui reste à définir), ce qui constitue une « contrainte amont » ;
3. ressembler à la réalité (dans un sens qui reste à définir), ce qui est une autre « contrainte amont ».

Chacune de ces exigences a sa légitimité, et son degré d'opportunité. Mais bien sûr, le praticien doit choisir, et il ne peut attendre d'un seul et unique modèle que ces trois contraintes soient satisfaites simultanément de façon optimale : par exemple, « ressembler à la réalité » et simultanément « être régulier » ne pourrait être envisagé que si la réalité était effectivement régulière, ce qui n'a rien de général concernant des variables naturelles ; ou encore, la « précision^[77] » d'un modèle n'implique nullement qu'il doive « ressembler » à la réalité. La figure ci-dessus illustre sommairement ces réflexions :

1. les trois premiers modèles sont des courbes indéfiniment dérivables : elles visent donc à satisfaire une propriété de régularité maximum. Elles respectent les huit données (la seule information réellement disponible), mais leur texture ne ressemble en rien à celle de la VR et, par ailleurs, elles ne correspondent pas à l'idée intuitive de ce que l'on pourrait appeler précision ;
2. le quatrième modèle satisfait à une contrainte de précision, au sens du krigeage. Il s'agit d'un profil dérivable et de dérivée continue, donc dans une certaine mesure qui satisfait à des contraintes de régularité. En revanche, ce profil ne « ressemble » pas à la réalité (ou plutôt : à la VR) en ce qui concerne sa texture, c'est-à-dire ses comportements de détail ;
3. les deux derniers modèles, eux aussi dérivables, cherchent à restituer la texture de la VR^[78], mais cette restitution se fait au détriment de la précision.

Ces exemples pourraient être multipliés à l'infini : c'est au praticien, et à lui seul, qu'il appartient de faire le tri, car les données à elles seules ne permettent pas de faire un choix univoque. Qui plus est, il faut se rappeler que presque toujours, la VR n'est que très partiellement reconnue par un échantillonnage nécessairement limité, de sorte que les « contraintes amont » non seulement ne peuvent être satisfaites, mais ne peuvent être définies qu'en référence non pas à la VR elle-même, mais à l'idée que s'en fait le praticien. Cela est particulièrement vrai pour la texture de la VR, c'est-à-dire son comportement de détail, qui est par nature inaccessible expérimentalement ; c'est pourquoi l'effort de modélisation doit être aidé par un dialogue permanent avec les naturalistes (selon les cas, géologues, géophysiciens, météorologues, économistes, etc.), qui seuls peuvent apporter ce complément d'information absent des données et pourtant indispensable. Une des particularités de la démarche géostatistique est de mettre en lumière de façon immédiate cette problématique qui, en fait, concerne l'ensemble des mathématiques appliquées.

Domaine de validité du modèle

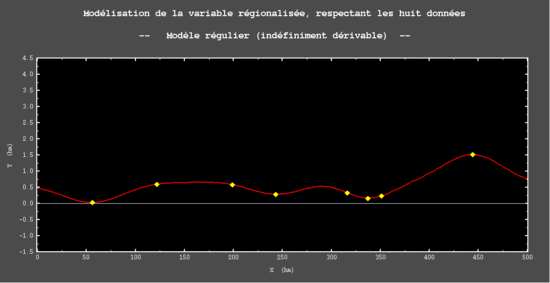Image actuellement inadéquate, WikiCommons s'obstinant à refuser de charger un gif animé...

Cette animation rapide illustre comment s'exerce l'effet de conditionnement sur les différentes représentations que l'on peut se faire de la réalité. Comme il était prévisible, les valeurs de la « carte » sont le plus fortement contraintes à proximité d'une donnée et, a contrario, les modèles peuvent proposer des valeurs extrêmement différentes lorsqu'on s'éloigne de tout point de mesure : cela est très clair en ce qui concerne l'extrapolation, ici par exemple pour des valeurs d'abscisses inférieures à 30 ou supérieures à 470 hm. Mais on peut noter que ces très importantes fluctuations numériques peuvent se manifester même en interpolation, en fonction de la densité des données conditionnantes ou de leurs dispositions relatives : c'est ce qui se passe par exemple vers l'abscisse 430 hm, qui pourtant aurait pu sembler suffisamment proche d'un point de donnée. En contrepartie, l'agrégat de trois données entre les abscisses 320 et 360 hm occasionne un conditionnement très fort, de sorte que toutes les cartes quelles qu'elles soient présentent des valeurs très semblables sur cet intervalle. Les « arrêts sur image » ont pour but de souligner que cet effet de conditionnement a lieu quels que soient les modèles adoptés pour tracer le profil, c'est-à-dire en particulier quels que soient l'allure générale et la texture des cartes. Cependant, on pourra noter sur cet exemple un phénomène souvent observé empiriquement : ce sont les modèles les plus réguliers mathématiquement (indéfiniment dérivables, en l'occurrence) qui occasionnent les fluctuations numériques les plus considérables et, on peut le supposer, les moins réalistes. En d'autres termes et pour utiliser des termes anthropocentriques, un modèle très régulier se laisse moins facilement contraindre par la réalité et cherche plus fortement à s'imposer à l'utilisateur.

À titre de première conclusion, on a donc souligné les risques que font encourir ce qui a été appelé l'« extrapolation physique », et mis en évidence que ce risque peut se manifester y compris à l'intérieur du domaine échantillonné, en fonction de la configuration géométrique des données.

Mais cet exemple très simple permet aussi d'illustrer les dangers de l'« extrapolation méthodologique ». Ainsi, puisque les modèles proposés ici sont tous au moins dérivables, on peut s'interroger sur la signification que pourrait prendre leur dérivée. Même si cela n'a pas de sens clairement défini de parler de dérivée d'un phénomène, on pourrait supposer que la dérivée du modèle (qui par hypothèse existe mathématiquement) donne un aperçu plausible d'une pente moyenne de la VR, dans un sens qu'il faudrait préciser[79]. La figure ci-contre montre combien cette hypothèse est risquée. Il s'agit d'un zoom réalisé autour du dernier point de donnée de la figure précédente, et qui montre qu'il peut y avoir des différences considérables au niveau des pentes des différentes « cartes », y compris si on se situe exactement en un point de donnée. En fait, en voulant interpréter la dérivée de la carte, on invoque une propriété analytique du modèle qui sort largement du cadre dans lequel le modèle a été effectivement ajusté. Naturellement, les risques de transgression du seuil de réalisme seront accrus si on sollicite une propriété encore plus exigeante : si la dérivée du modèle a peu de chances de correspondre à une pente au niveau du phénomène physique, il est encore plus improbable que la dérivée seconde puisse être associée à une notion de courbure, en dépit de ce qu'expriment les mathématiques pures... Le déroulement d'une étude géostatistique demande donc, une fois de plus, de satisfaire à une recherche d'équilibre : d'une part, il est légitime d'essayer d'employer le modèle à exprimer des propriétés du phénomènes que ne pourraient pas mettre en évidence une simple manipulation des données brutes ; mais d'autre part, il est fondamental de se donner les moyens de contrôler les conclusions du modèle en revenant à ce qui fonde l'ensemble de la démarche, à savoir la VR elle-même.

Le conditionnement par les données s'exerce sur la valeur de la carte, mais non sur sa pente.

Rappel de notations

Lorsque cela ne soulèvera pas d'ambiguïté, nous respecterons dans la suite les habitudes de notation en usage dans la littérature géostatistique francophone :

• en toute généralité, une VR (en tant que fonction) sera désignée par la lettre z^[80]. Toutefois, on peut aussi choisir une notation rappelant la nature physique de la VR : cela est opportun dans le cas d'une étude multi-variable, pour éviter de surcharger z par un indice rappelant de quelle composante il s'agit ;
• on adopte en général une notation unidimensionnelle pour représenter les coordonnées, même si l'espace de départ est à plusieurs dimensions. Ainsi, toujours si cela ne soulève pas d'ambiguïté, désignera en général un point de l'espace de départ, et non la seule abscisse de ce point. De même, et sauf indication contraire explicite, la notation désignera une paire de points de l'espace de départ ;
• plus généralement, un indice appliqué à une coordonnée numérote le point concerné, non une de ses coordonnée. Ainsi, la suite décrit un n-uplet de points de l'espace de départ ;
• pour désigner la valeur prise par la VR en un point indicé, on adoptera également l'usage^[81] de simplifier l'écriture attendue en . Ainsi,

• ces conventions s'étendent naturellement au cas continu. Ainsi, pour une VR scalaire, l'intégrale^[82]

représente la valeur moyenne de la VR sur le domaine , sans préjuger de la dimension de l'espace de départ. Quant à la notation , elle représente la mesure (au sens mathématique) du domaine  : longueur, aire ou volume, selon que l'espace de départ est à une, deux ou trois dimensions.

Attributs d'une VR

Une VR ne saurait se limiter à une collection de valeurs numériques implantées en des points de l'espace de travail, car « les valeurs numériques ne sont pas le réel, mais une première image (analytiquement très riche, structuralement très pauvre) de celui-ci^[83] » : seulement une première image. Certes, rien n'interdirait de dérouler les algorithmes géostatistiques en se fondant uniquement sur cet aspect purement quantitatif, et en se fiant exclusivement à l'exactitude mathématique des opérations ; pourtant, il est clair qu'on se priverait ce faisant d'une information importante, absente des données et pourtant capitale pour assurer la pertinence du traitement futur de ces données. Aussi, même si le jeu de données brutes constitue la seule information incontestable^[84] et le dernier recours en cas de doute méthodologique, « le reste — les idées que nous pouvons nous faire sur la genèse et la structure du phénomène, et, plus généralement l'intuition physique que nous nous en formons — n'en continue pas moins à jouer en coulisse un rôle des plus importants. C'est en général dans ce trésor archétypique que nous aurons des chances de trouver les schèmes ou les principes moteurs de modèles vraiment adaptés^[83]. »

Cette information la plupart du temps qualitative, qui rajoute du sens aux données traitées, ne peut être acquise que par le dialogue entre le géostatisticien d'une part, et d'autre part le naturaliste, ou plus généralement le praticien qui a soumis le problème. Cette phase de dialogue est d'autant plus cruciale que, si on la néglige, il n'y aura en général aucun garde-fou pour protéger au cours des développements ultérieurs contre des traitements dépourvus de signification physique, de sorte que l'on risque de franchir le « seuil de réalisme » sans même en avoir conscience. La difficulté est que le géostatisticien, surtout s'il aborde un domaine d'application nouveau pour lui, ne saura pas nécessairement de quoi il doit s'inquiéter auprès du naturaliste ; et inversement, le naturaliste qui n'est pas au fait des théories mises en œuvre ne saura pas nécessairement sur quel point sensible il doit mettre l'accent.

Il existe cependant des constantes, des caractéristiques de la VR que le géostatisticien doit connaître quelle que soit l'étude entreprise, sous peine de perdre d'emblée tout contact avec le sens physique de ses opérations. On peut ainsi dans tous les cas distinguer trois attributs (nature, domaine et échelle de travail, support) et une propriété (additivité), dont le géostatisticien doit avoir connaissance et garder le contrôle.

Nature

La nature de la VR ne semble pas poser de problème en général : il s'agit tout simplement de notifier dans un premier temps de quelle variable d'intérêt on parle, et de préciser l'unité employée pour mesurer les données (ou les différentes unités dans le cas d'une VR multivariable).

Il importe bien sûr que dans un jeu de données, tous les échantillons soient de même nature et s'expriment dans les mêmes unités :

• mêmes unités : l'accident célèbre de Mars Climate Orbiter est une illustration spectaculaire de l'impact catastrophique d'un mélange de deux systèmes de mesures dans une chaîne de traitements numériques. Et même si le déroulement des calculs est effectué correctement, encore ne faut-il pas se tromper sur l'unité en laquelle sont exprimés les résultats, comme en atteste la perte de Kosmos 419. Il ne s'agit pas ici de vues de l'esprit, mais d'erreurs avérées, concrètes, et qui ont eu un coût considérable ;
• même nature : ainsi, pour l'estimation d'un gisement d'uranium, on ne mélangera pas des données de teneurs et des données de radioactivité, quand bien même ces deux informations sont presque équivalentes en ceci qu'elles traduisent à peu de chose près le même phénomène physique^[85]. Faire un amalgame serait une erreur ; mais il serait par ailleurs regrettable de se priver du surplus d'information que constituent deux variables distinctes répondant au même objectif. Ici, la réponse méthodologique à cette difficulté est très simple, et très courante^[86] : il faut considérer le problème comme étant multivariable. Par exemple, la VR utilisée pour rendre compte du gisement d'uranium sera finalement à deux composantes (teneur, radioactivité) et ultérieurement, le formalisme de la géostatistique multivariable^[87] permettra de traiter ces deux composantes simultanément, en particulier en modélisant puis en utilisant leur forte corrélation.

Il est vrai que le formalisme de traitement multivariable est plus lourd et parfois plus délicat à manipuler que l'étude d'une variable scalaire unique^[88]. On pourrait alors être tenté de convertir a priori des données initialement disparates en une seule unité, et ensuite traiter le problème dans une optique monovariable^[89]. Cette technique n'est pas recommandable : elle cache le caractère hétérogène du matériau que l'on manipulera par la suite, et donc fait disparaître une information peut-être importante. En fait, il est recommandé de pousser la prudence jusqu'à distinguer des échantillons pourtant rigoureusement de même nature, mais prélevés avec des appareillages et/ou à des époques très différents. Il serait par exemple imprudent d'entreprendre une étude de cartographie sous-marine en mélangeant des données datant des années 1960 (avant le positionnement par GPS, les erreurs de localisation pouvaient être de plusieurs hectomètres en pleine mer) et des données actuelles ou, plus exactement, il est souhaitable de « faire comprendre » aux traitements futurs que les données sont de qualités différentes.

Ce dernier exemple attire l'attention sur un point souvent négligé, mais qui est d'importance pour un travail géostatistique minutieux. Idéalement, il serait souhaitable qu'à toute variable soit associé un indicateur de sa qualité. Après tout, la plupart des constructeurs fournissent à l'intention des professionnels des informations sur la précision de leurs instruments, et il serait dommage de ne pas utiliser cette connaissance. Dans les cas les plus élémentaires, il s'agit simplement d'une marge d'erreur, d'un intervalle de confiance unique pour toutes les mesures. Mais la situation peut être beaucoup plus complexe : ainsi, pour des mesures de bathymétrie effectuées par un navire le long de profils parallèles, il est probable que les erreurs de localisation le long d'un même profil seront fortement corrélées^[90], alors qu'elles seront peut-être indépendantes entre deux profils. C'est une information très importante, qui ne saurait en aucun cas être contenue dans les seules valeurs de la bathymétrie mesurées. Il serait donc très profitable, dans la mesure du possible, d'associer à la VR d'intérêt une seconde VR qui quantifierait la précision de la première, autrement dit de travailler sur une VR bidimensionnelle (valeur, précision) : cette démarche, qui certes rajoute de la lourdeur aux calculs, n'est pas fréquemment entreprise, mais il est important de savoir qu'elle est accessible aux outils de la géostatistique.

Dernier point concernant la nature de la VR : contrairement à ce que serait une approche purement mathématique qui ne s'attacherait qu'aux valeurs numériques indépendamment de leurs interprétations et de leurs unités, la démarche du géostatisticien est guidée par la signification et la nature de la donnée qu'il examine. Même si la courbe est la même (à d'éventuels changements près d'unités sur les deux axes), le praticien ne réagira pas de la même façon devant le tracé d'une série temporelle selon que celle-ci décrit la température d'un malade, le cours de la bourse, la position d'une particule ou une séquence de précipitations sur un bassin versant... Car tout domaine de travail a ses spécificités de même que les spécialistes de chaque domaine ont leurs expériences propres, et il serait regrettable voire désastreux de se priver de ce surcroît de connaissance. La prise en compte de la nature de la VR constitue une sécurité, une protection contre le risque de dépasser le seuil de réalisme : toutes choses égales par ailleurs, on pourra probablement accepter des valeurs modélisées négatives s'il s'agit d'altitudes (il s'agit de profondeurs sous-marines, simplement) ; cela deviendra préoccupant, quoique théoriquement acceptable, s'il s'agit de bénéfices d'une entreprise ; et cela sera parfaitement absurde s'il s'agit de pressions atmosphériques. Bien plus : il est probable que devant un profil représentant des altitudes et tracé sans préciser les unités, le praticien ne réagira pas de la même façon s'il pense qu'il s'agit d'un profil d'extension kilométrique ou qu'il s'agit du profil d'un continent entier : une carte sans unités pourrait satisfaire le mathématicien pur, mais elle est presque sans utilité pour le praticien — en tout cas dans l'optique de la géostatistique.

Une VR (série chronologique) anonyme : Température d'un malade ? de l'atmosphère ? Cours de la bourse ? Séquence de précipitations ?

Une carte sans légende est inutilisable, même s'il est possible de lui appliquer des traitements mathématiques théoriquement corrects.

Domaine, et échelle de travail

Contrairement au domaine (mathématique) de validité d'un modèle, le domaine de la VR — considérée cette fois comme un objet physique — est une notion ambivalente.

Point de vue « amont »

Il s'agit dans un premier temps de la portion d'espace et/ou de temps sur laquelle les données sont disponibles. Naturellement, les données étant toujours constituées d'un ensemble fini de valeurs numériques, il faut plutôt comprendre le domaine comme une enveloppe des points de données, en général dilatée (au sens morphologique). C'est donc une définition qui laisse place à une part d'arbitraire, et qui est étroitement associée à la notion intuitive, très courante mais imprécise, de « zone d'influence » des données^[91] ; en d'autres termes, le domaine (de définition) de la VR est la portion d'espace à l'intérieur de laquelle on est fondé à penser que les données disponibles apportent une information significative. Quelque floue et finalement insatisfaisante qu'elle soit, cette formulation présente un intérêt indéniable : elle souligne que l'extension du domaine où la VR peut « raisonnablement^[92] » être considérée comme connue ne dépend pas seulement de la géométrie de l'information, mais aussi de la structure intrinsèque de la variable étudiée : il est clair en effet par exemple que pour un schéma d'échantillonnage donné, le domaine d'une variable très erratique devra être considéré comme moins étendu que celui d'une variable fortement structurée et peu fluctuante ; autrement dit, en un point éloigné^[93] des points de mesures, les données disponibles apportent moins d'information si la VR est erratique que si elle est peu fluctuante^[94].

Cette remarque attire l'attention sur un point méthodologique très important. Elle exprime en effet que la délimitation du domaine d'une VR ne devra pas dépendre seulement de l'information déjà disponible (la géométrie de l'échantillonnage), mais aussi de la structure de la VR, qui est une caractéristique que précisément on cherche à mettre en évidence par le traitement géostatistique. Il s'agit bien d'une « contrainte amont », en ceci qu'elle existe bel et bien préalablement au départ de l'étude et indépendamment des choix du géostatisticien[95] ; mais elle constitue seulement une information future qui se dévoilera progressivement et qu'il faut savoir anticiper. Autrement dit, au début d'une étude, on ne sait pas a priori avec précision quel est le domaine de validité des opérations que l'on va entreprendre, du moins en se fondant sur les seules valeurs numériques disponibles[96]  : une notion que l'on aurait pu croire basique (le domaine de définition de la VR) est en réalité en partie tributaire de ce que l'étude ultérieure mettra en évidence. C'est pourquoi il est normal, en réalité nécessaire et fructueux, qu'une étude appliquée ne se déroule pas de façon linéaire, mais procède par retours en arrière et réajustements des modèles en fonction de la progression du travail[97]. La confrontation du domaine avec la géométrie de l'information disponible constitue une première approche de la très importante notion d'échelle de travail. Par exemple, si le domaine reconnu est le territoire français métropolitain, il est évident que l'on en aura une meilleure connaissance avec 551 000 données réparties sur une grille carrée de côté 1 km qu'avec par exemple 95 données implantées à raison d'une par département. De façon très grossière, ainsi que le suggère cet exemple simpliste, on peut dans un premier temps rapprocher la notion d'échelle de travail de celle de densité d'information. Toutefois, cette approximation n'est plus valable dès que l'échantillonnage est réparti de façon hétérogène : ainsi, lors d'une campagne de bathymétrie réalisée sur des profils de navigation parallèles et largement[93] espacés, profils eux-mêmes très densément[93] échantillonnés, il est très difficile de définir une échelle de travail significative globalement ; clairement, on aura une échelle très fine[98] à proximité[93] immédiate des profils, et lâche lorsqu'on se place loin[93] de tout profil. Cette problématique est éclairée en géostatistique par l'important concept de variance d'estimation, un outil quantitatif qui est très étroitement associé à l'échelle de travail, et qui constitue un premier indicateur fondamental pour mesurer[99] la qualité et la fiabilité des modélisations entreprises. Point de vue « aval » Mais le domaine de la VR dépend aussi du problème posé, et on rejoint ici la réflexion sur le domaine de définition (mathématique) du modèle. Certes, la portion d'espace sur laquelle on s'interroge est souvent très similaire au domaine sur lequel on dispose des données : c'est en particulier le cas lorsqu'on réalise des interpolations. Ainsi par exemple, l'extension d'un gisement minier que l'on cherche à estimer sera très voisine de l'enveloppe des données disponibles ; de même, on ne réalisera pas une carte topographique des Alpes avec des données mesurées en Beauce... Pourtant, cette exigence de bon sens ne peut pas toujours être satisfaite. C'est parfois la nature même du problème qui exige que le domaine étudié excède le domaine reconnu par les données : c'est le cas en particulier dès qu'il s'agit de faire des prévisions. On pensera à des exemples immédiats en économie, en épidémiologie, en météorologie et climatologie, lorsque l'espace de travail est le temps. Mais il y a des circonstances plus cachées. Par exemple, lorsqu'on cherche à estimer les réserves d'un gisement, le domaine sur lequel on souhaite réaliser l'inventaire de la substance à exploiter correspond évidemment à la géométrie du gisement, sauf que cette information n'est pas disponible : la frontière du gisement n'est pas connue[Voir 19]. La seule chose qu'il soit possible d'affirmer, c'est si un forage donné est ou n'est pas dans le gisement. Bien plus, les informations disponibles sont en général toutes intérieures au gisement, pour la simple raison que les industriels n'aiment pas financer des forages ou des analyses effectués dans du stérile : autrement dit, la frontière du domaine ne peut être évaluée que par extrapolation, ce qui est en général source d'instabilités numériques. Au point de vue méthodologique, il y a encore plus dangereux, puisque la définition même du domaine repose en général sur un seuil de teneur[100] ; or cette variable — la teneur — constitue précisément le sujet de l'étude[101] : on se trouve donc dans le meilleur des cas exposé à des effets de bord, souvent imprévisibles et qui parfois masquent complètement les informations utiles. Mais plus profondément, on voit se mettre en place un obstacle théorique qui s'apparente à l'argument circulaire, soit, en caricaturant à peine : « on a besoin de la solution (les teneurs en tout point) pour poser correctement le problème (délimiter le volume sur lequel on va estimer le gisement) » ; si l'on s'en tient aux seules données numériques et si l'on ne veut pas commettre de faute méthodologique grave, on se trouve dans une impasse. Le renfort d'informations extérieures aux données numériques est alors, ici, absolument indispensable[102]. Par ailleurs, même en demeurant sur un domaine d'étude très semblable au domaine reconnu, on peut vouloir changer d'échelle de travail. Ainsi, sur l'exemple proposé ci-contre, si on souhaite réaliser une cartographie des valeurs de géochimie sur une maille carrée de côté 5 m, cela signifie que l'on veut un résultat à une échelle environ 15 fois plus fine[98] que l'échelle de l'information initiale, puisque la répartition des données est en moyenne équivalente à une grille de 75 m[103]. Il y a un point crucial à noter ici : strictement rien, au démarrage de l'étude et sur la base des seules 412 données, ne permet de savoir si le projet d'affiner par un facteur 15 l'échelle initiale est légitime ou non. Il est clair que la justification de cette opération dépendra étroitement de la structure de la variable étudiée, et qu'une opération acceptable pour une variable très fortement structurée[104] deviendra irréaliste pour une variable très erratique ; le problème étant que cette structure ne peut être appréhendée que sur la base des données disponibles, c'est-à-dire de l'échelle la plus lâche[98] : on est ici confronté à une problématique très voisine méthodologiquement de ce qui se rencontre en théorie du signal. Une nouvelle fois, le praticien doit invoquer son expérience, et savoir faire preuve d'anticipation, avant que des manipulations critiques[105] puissent lui permettre — mais seulement a posteriori — de juger de la pertinence de ses choix.

Domaine à estimer et schéma d'échantillonnage

Exemple-type d'un dispositif d'échantillonnage de mesures géochimiques en vue d'une estimation : 412 données irrégulièrement réparties, et domaine imposé, d'une superficie totale 2,28 km2, situés à l'ouest du Vulcano. Si ces données étaient réparties selon une grille carrée, le carré ferait environ 75 m de côté, ce qui constitue un premier élément de l'échelle de travail, à comparer ultérieurement avec les distances caractéristiques du phénomène qui seront mises en évidence en cours d'étude.

Illustration sommaire

Sur la base des données précédemment évoquées (géochimie sur l'île de Vulcano), les images suivantes illustrent quelques problèmes liés à la représentation d'une VR et à ses attributs :

Panoplie de quatre représentations d'un même phénomène (domaine imposé)	Cette figure simpliste illustre une des premières finalités d'un travail de géostatistique élémentaire : « remplir les lacunes d'information ». En effet, outre les limites du domaine qui sont ici imposées, la seule chose qui soit réellement connue est l'ensemble des 412 données, repéré sur la première vignette : mais cette information objective ne peut pas être cartographiée sur l'ensemble du domaine, puisque celui-ci constitue un continuum. Cette première image est très difficile à lire, et à interpréter structuralement[106]. La seconde vignette propose une première piste de visualisation : une partition de Voronoï, avec un codage de couleurs permettant de se faire une idée de la structuration spatiale de la VR. Mais il va de soi qu'il s'agit d'une représentation très grossière, et que personne n'imaginera que la réalité (telle qu'on pourrait l'observer si on effectuait des mesures supplémentaires) puisse ressembler effectivement à ce que montre cette image. Il s'agit d'une première modélisation, d'une première interpolation, du reste extrêmement contestable. Elle possède en effet des propriétés mathématiques (elle est constante par morceaux) qui n'ont en l'occurrence aucune chance de correspondre à une réalité physique[107].
Figure 1 : carte d'implantation des données ; Figure 2 : représentation des « zones d'influence », définies par un diagramme de Voronoï. À chaque cellule est associée la valeur de la donnée qui lui appartient ; Figures 3 et 4 : deux illustrations de la même VR, à des échelles respectivement de 75 m et 5 m.
Les deux dernières vignettes représentent exactement le même ensemble de valeurs, qui sont une interpolation construite sur la base des 412 données. Seules diffèrent les échelles de représentation, respectivement 75 m et 5 m. La première de ces valeurs a été choisie parce qu'elle équivaut à ce que serait une répartition régulière des 412 données : ainsi, il y a le même nombre de valeurs de la VR représentées sur les vignettes 2 et 3[108]. On observe que ces paramètres « aval », arbitraires, ont un impact non négligeable sur l'aspect des cartes. On se doute bien que l'aspect en damier de la troisième vignette est un pur artefact ; mais il faut bien voir qu'un effet tout-à-fait similaire apparaîtrait sur la quatrième vignette si on l'observait plus en détail... Ces effets, conséquences ici bien visibles du mode opératoire, sont strictement inévitables, et il appartient de ne pas leur attribuer une signification physique qu'ils ne sauraient avoir.

Support

Mathématiquement, une VR sera une fonction sur l'espace de départ, donc prendra une valeur en tout point de cet espace. Dans ces conditions, « connaître » certaines valeurs de la VR signifierait que l'on a réalisé effectivement la mesure en un nombre (nécessairement fini) de points. Or, on ne peut jamais effectuer une telle mesure : même pour des variables aussi simples que des cotes topographique, des températures ou des pressions, les valeurs communiquées par l'appareillage ne sont jamais rigoureusement ponctuelles, ne serait-ce qu'en raison de la dimension de l'appareil de mesure ; et de la même façon, une mesure temporelle n'est jamais rigoureusement instantanée, tout dispositif présentant un effet d'hystérésis plus ou moins prononcé. On peut certes considérer que dans les premiers exemples qui viennent d'être cités, il n'y a pas de danger à considérer les données comme sensiblement ponctuelles, mais il y a des situations où cette approximation n'est plus acceptable. Ainsi, en géostatistique minière, une analyse minéralogique est toujours effectuée sur un échantillon d'un certain volume (une carotte, par exemple), et la valeur de la teneur qui est obtenue est en fait, en l'occurrence, la moyenne des teneurs ponctuelles présentes sur cette carotte^[114]. La valeur qui est mesurée est donc tributaire de la variable d'intérêt (la teneur), mais aussi de paramètres contingents comme la taille et la forme de la carotte. Même chose en météorologie, où la pluviométrie mesurée n'est pas une quantité d'eau tombée instantanément^[115], mais le cumul de ce qui est tombé durant une période arbitrairement fixée. Comme dernier exemple plus complexe, on peut enfin citer la mesure de l'élévation de l'océan, actuellement connue avec une précision centimétrique : une telle précision, concernant un phénomène spatio-temporel qui en un point de coordonnées fixées peut connaître des fluctuations de quelques dizaines de mètres, n'a de sens que si la variable d'intérêt est définie comme une moyenne calculée sur un support géographique et un intervalle de temps bien spécifiés^{[Voir 20]} ; et la robustesse de cette moyenne sera clairement entièrement dépendante^[116] de ce support et de cet intervalle.

Il peut aussi se présenter des situations dans lesquelles la nature même de la VR interdit d'envisager des mesures ponctuelles, même approchées. Par exemple, en prospection d'uranium, la valeur de radioactivité mesurée en un point ne dépend pas seulement de l'activité de la radiosource implantée en ce point^[117], mais de tout l'environnement, et ceci en suivant une loi de pondération parfaitement connue des physiciens. Même chose en ce qui concerne la géophysique (gravimétrie ou magnétisme) : les valeurs observées en un point sont révélatrices de tout un environnement, étant bien entendu que des régions plus lointaines ont une influence plus faible que la proximité immédiate du point où est effectuée la mesure^{[Voir 21]}.

De la sorte, toute mesure est en réalité une régularisation (un lissage) plus ou moins accentuée des valeurs ponctuelles de la VR (au sens mathématique). Cet effet de régularisation est toujours inhérent au processus de réalisation de mesures, et parfois de surcroît à la nature du phénomène mesuré. Il peut se modéliser^[118] facilement : une mesure instrumentale apparaît toujours mathématiquement comme le produit de convolution^[119] de la VR (théoriquement ponctuelle) par un certain opérateur^[120] dépendant du dispositif de mesure et/ou de la physique du phénomène. Cela étant, deux remarques :

• en fait, il arrive souvent que, par comparaison à l'échelle de travail, le support de régularisation soit suffisamment petit pour qu'il soit acceptable de traiter les données comme effectivement ponctuelles. Il s'agit très exactement d'une approximation, adoptée pour simplifier le formalisme théorique, et qui demeure légitime tant qu'elle n'est pas remise en question soit par des informations objectives nouvelles, soit par des incohérences lors de la mise en œuvre du modèle ;
• même lorsqu'une valeur numérique représente un support étendu, il n'est pas interdit de l'affecter à un point de l'espace géographique. Par exemple, la valeur moyenne d'une maille d'un réseau carré pourra être affectée au centre de la maille ; la teneur moyenne d'une carotte sera affectée (par exemple) aux coordonnées du centre de gravité de cette carotte ; etc. Ce point de vue est une généralisation du concept de moyenne glissante, et c'est le plus fréquemment employé : bien que les données ne soient pas ponctuelles, on garde ainsi le même espace (« géographique ») de départ, et on continue à bénéficier de sa métrique. Mais on peut aussi faire un choix différent : on peut décider de considérer que les objets (les singletons) de l'espace de départ sont désormais les supports de régularisation ; on quitte ainsi le domaine du continu pour se limiter à des statistiques discrètes, et c'est ce qui est proposé par exemple dans la figure précédente, avec le découpage en polynômes de Voronoï^[121] . Cette approche, rarement mise en œuvre en pratique, a cependant eu historiquement une importance théorique considérable, puisque c'est elle qui a permis l'introduction du concept de variance de dispersion, essentiel pour dégager les fondements de la géostatistique intrinsèque.

La prise en compte d'un support de régularisation introduit donc un nouveau facteur d'échelle^[122]. Ce nouveau facteur intervient de façon plus discrète que les autres lorsqu'il s'agit de définir les conditions de traitement des données, par exemple lors d'estimations ou de simulations numériques : le choix des points de données à utiliser pour réaliser une interpolation est beaucoup plus tributaire de la structure du phénomène et de la densité d'information que du support ; en revanche, le support a une importance considérable sur les statistiques réalisées sur les données, et particulièrement en ce qui concerne la variabilité. Ainsi un des premiers apports historiques notables de la géostatistique, dans le domaine minier, a consisté à expliquer et modéliser le fait que les teneurs mesurées sur des lames minces étaient plus fluctuantes et moins structurées que les teneurs (du même minerai, sur la même mine) mesurées sur des carottes^[123].

Dernière remarque : le phénomène de régularisation a un impact direct sur la structure des outils d'investigation structurale, en particulier le variogramme, et cet impact caractéristique est très facile à modéliser^[124]. Aussi, inversement, les outils géostatistiques peuvent-ils permettre dans certains cas de diagnostiquer que des mesures que l'on croyait quasi-ponctuelles sont en réalité des régularisées^[125].

Additivité

Une VR sera dite « additive » si la valeur globale qu'elle prend sur un ensemble de domaines géographiques disjoints est égale à la somme des valeurs prises sur chacun de ces domaines^[126]. Par exemple, dans une mine à ciel ouvert, le tonnage de métal contenu dans un gradin est bien égal à la somme des tonnages sur chacun des blocs distincts composant ce gradin : la quantité de métal est une variable additive ; plus simple encore dans cet exemple, il en est de même du volume. De la même façon, des quantités de chaleur ou d'électricité, des masses, les volumes produits par un puits de pétrole (en fonction du temps), etc. sont des variables additives. Cette propriété est particulièrement intéressante, parce qu'elle rend très faciles les mécanismes de changements d'échelles en gardant un sens physique aux opérations.

Sans être additives, il existe des variables qui bénéficient également de bonnes propriété, parce qu'on peut se ramener au cas précédent moyennant une transformation simple. C'est le cas par exemple des teneurs : la teneur globale d'un ensemble de plusieurs blocs n'est pas égale à la somme des teneurs de chacun d'eux ; mais si on multiplie chacune des teneurs par le volume du bloc correspondant^[127], on obtient une masse qui, elle, est une variable additive, et la somme des masses divisée par la somme des volumes donne la teneur globale. Cette fois, le résultat final est obtenu comme étant non plus une somme, mais une moyenne pondérée ; notons d'ailleurs que si tous les blocs étaient de même volume, il s'agirait d'une moyenne arithmétique simple. Cette situation se retrouve par exemple en hydrogéologie avec une variable comme la porosité, en agriculture avec des rendements à l'hectare, en épidémiologie avec des nombres de malades par commune ou par département, en environnement avec des taux de pollution. Dans ce dernier cas, on peut également se ramener au cas additif temporellement s'il s'agit d'une substance qui ne se dégrade pas, comme par exemple un métal lourd, etc. On note dans tous les cas que pour revenir à une grandeur additive, il faut utiliser une variable auxilliaire, souvent de nature géométrique, comme l'aire ou le volume, la durée, ou la masse : encore faut-il naturellement que cette variable auxilliaire ait été correctement échantillonnée^[128], et c'est un cas où le géostatisticien peut être de bon conseil auprès de son client dès la campagne de mesures.

L'intérêt méthodologique d'une variable additive est considérable. En effet, en effectuant des cumuls de cette variable sur des domaines aussi variés que possible, on obtient toujours des valeurs qui ont un sens physique clair, et qui par ailleurs peuvent faire — au moins par la pensée^[129] — l'objet de contrôles expérimentaux. Par ailleurs, les outils les plus simples de la géostatistique linéaire^[130] permettent de formaliser théoriquement ces transformations (cumuls ou moyennes pondérées) et de les rendre opératoires. La seule limite, contingente, à cette phase de contrôle est la quantité d'information disponible.

Pour rapprocher d'une notion courante, on peut dire que les VR additives ou qui peuvent être ramenées à un comportement additif ont la particularité de ne pas provoquer de phénomène d'émergence.

Malheureusement^[131], beaucoup de variables ne sont pas additives. Par exemple, une température non seulement n'est pas additive au sens strict, mais il n'est pas certain qu'une moyenne de températures ait une signification physique incontestable, que cette moyenne soit spatiale ou temporelle. Cela ne veut naturellement pas dire que cette moyenne sera sans utilité : on peut ainsi imaginer qu'elle prenne une place légitime dans (par exemple) des équations d'évolution ; on peut même (au moins par la pensée) la contrôler « sur le terrain^[132] » et donc elle a une signification objective^[133] ; mais il est impossible d'imaginer un phénomène physique qui, en un lieu donné et a une date donnée, prenne la valeur indiquée par cette moyenne spatio-temporelle^{[Voir 22]} : cette valeur n'est donc ni plus ni moins que le résultat d'un processus de calcul.

Un autre exemple de VR non additive, beaucoup plus complexe à traiter, est fourni par l'hydrogéologie avec la variable perméabilité. Il n'y a pas de relations simples entre les différentes perméabilités mesurées à différentes échelles (microscopique et macroscopique) ; il n'y a pas d'expression simple permettant de relier la perméabilité sur deux unités de volume et la perméabilité résultante sur l'union de ces deux volumes, et encore les expressions disponibles dépendent-elles de la dimension de l'espace^[134]. Dans ces conditions, il est clair qu'une somme (éventuellement pondérée) de deux perméabilités n'a pas de signification physique et, même si l'on n'engage aucun changement d'échelle, une simple interpolation peut déjà être problématique : en l'occurrence, ce ne sont pas les outils mathématiques qui laissent voir des faiblesses, mais c'est un phénomène physique qui révèle son extrême complexité. Dans ces conditions, et plus généralement pour les VR non additives, il va de soi que le travail géostatistique doit être mené avec un maximum de précautions.

D'une variable régionalisée à une fonction aléatoire

Motivation, et notations

Les raisons d'une modélisation probabiliste

Dès les débuts de la géostatistique^[135], les limites inhérentes à un travail fondé exclusivement sur le modèle primaire sont apparues à la fois au plan théorique et au niveau de la mise en œuvre. Les formalismes développés, et qui constituent la matière de la géostatistique transitive, s'expriment essentiellement pour des informations disponibles sur une maille régulière (éventuellement avec des lacunes), ce qui peut convenir pour certains problèmes (analyse d'image, par exemple, ou estimations de surfaces ou volumes) mais n'est pas adapté à des échantillonnages irréguliers comme on en trouve dans la plupart des études : cette difficulté s'est rencontrée dès les premiers travaux appliqués, qui concernaient des estimations minières^[136]. Toutefois, il aurait pu être intéressant de chercher à résoudre ce problème purement technique en restant dans le cadre du modèle primaire, tant ce modèle paraît satisfaisant : il ne requiert en effet aucune hypothèse particulière relative à la structure de la VR étudiée, et les outils de la géostatistique transitive sont essentiellement adaptés à travailler sur un champ borné, ce qui correspond exactement au cadre d'une étude réelle.

Pourtant, un obstacle de fond apparaît dès que l'on souhaite évaluer la qualité des résultats proposés. En effet, qu'il s'agisse d'interpolation, d'estimation ou de toute autre opération algorithmique effectuée sur un jeu de données, il est clair qu'il n'est pas possible de se satisfaire de la production d'un seul nombre (ou une seule carte) ; encore faut-il que l'on dispose d'une mesure au moins indicative de la fiabilité de ce résultat. Or, un résultat profond apparaît ici, qui pose les limites de la méthode transitive : « Il est théoriquement impossible de déduire des mêmes données expérimentales à la fois une estimation et la précision de cette estimation^[137]. » En rester à une utilisation exclusive de la VR est sans issue : si nous « convenons de dire qu'un modèle est strictement objectif si ses critères de spécification ne font intervenir que des paramètres objectifs (identifiables à des grandeurs régionales) et des paramètres méthodologiques (imposés sans ambiguïté par le problème à résoudre et la méthode choisie) à l'exclusion de toute autre sorte de paramètres conventionnels », alors « il est clair qu'un modèle strictement objectif — et justement parce qu'il est strictement objectif — ne peut être que tautologique  : il ne fait que représenter sous une autre forme la même information, celle qui est contenue dans la donnée de la VR^[138] ».

Au point de vue théorique, il y a cercle vicieux. « En pratique pourtant, l'introduction de certaines hypothèses raisonnables d'approximation ou de simplification permet de briser le cercle^[139] » : ce sont les hypothèses anticipatrices, « avec leur fécondité et la vulnérabilité qu'elle implique^[139] ». Historiquement, pour des données disposées aux nœuds d'une grille régulière, la géostatistique a usé d'un subterfuge : considérer que l'origine de la grille a été choisie aléatoirement de façon uniforme^[140] ce qui confère ipso facto aux grandeurs régionales un statut aléatoire, et qui ouvre donc la porte à d'éventuels calculs de variances, c'est-à-dire d'outils de mesure de qualité. Cette démarche semble d'autant plus satisfaisante qu'elle n'implique aucune hypothèse a priori quant aux propriétés (statistiques, structurales) de la VR elle-même. En apparence, le problème est résolu, même si la réponse est fortement tributaire du caractère régulier de la maille d'échantillonnage : à l'évidence, il y a de nombreuses situations où supposer les données régulièrement distribuées ne constituera pas une approximation acceptable. Mais il y un résultat plus profond que l'approche théorique met en évidence^[140] : toutes choses égales par ailleurs^[141], la variance théorique d'un estimateur peut présenter des fluctuations numériques considérables et incontrôlables pour de faibles variations de la dimension de la maille. De façon imprévue, on se trouve dans ce que Matheron appelle une « situation préaléatoire » : « L'"idée de hasard" c'est-à-dire, en réalité, l'usage des modèles probabilistes, s'introduit en physique "lorsque des conditions initiales inséparables expérimentalement sont suivies ultérieurement d'une séparation manifeste des phénomènes observés"^[142]. » Et plus tard, lorsqu'on choisit de représenter la fonction structurale — qui est une grandeur régionale^[143] — par un modèle plus simple, on peut interpréter cette modélisation « comme un passage à l'espérance mathématique ». Le cadre probabiliste s'impose de lui-même en quelque sorte.

La géostatistique intrinsèque a choisi de franchir le pas et de se placer délibérément dans le cadre d'une modélisation probabiliste, et ce choix a pris place dès les débuts de la géostatistique. Les développements ultérieurs ont montré que, bien que fondé sur une théorie bien plus abstraite que la géostatistique transitive, ce formalisme est parfaitement opérationnel et ouvre davantage de perspectives. Le formalisme transitif peut être considéré comme étant à l'origine de la morphologie mathématique, et il présente un indéniable intérêt pédagogique ; mais dans le cadre de la géostatistique, il n'est plus guère utilisé que pour traiter des problèmes de nature géométrique.

Statut épistémologique

Le choix de la géostatistique intrinsèque est d'associer à toute VR une fonction aléatoire^[144] (FA), dont la VR sera considérée comme une réalisation.

Ce choix — car il s'agit d'une décision parfaitement arbitraire — est dicté seulement par des considérations opératoires. Il a été inspiré par les réflexions sur le statut de la VR, et a été conforté ultérieurement par la pratique et les développements de la géostatistique. Mais il ne signifie en rien que la réalité que nous étudions procède réellement d'un phénomène aléatoire. Du reste, affirmer que le réel est l'émanation d'une forme quelconque de hasard est une proposition qui n'est ni vérifiable, ni réfutable, et qui par conséquent sort du champ du discours scientifique. Ce qui peut faire l'objet d'un travail scientifique en revanche, c'est l'étude de l'adéquation d'un modèle aléatoire à la réalité étudiée. Ainsi, avec un degré d'approximation fixé, on peut contrôler si un modèle probabiliste permet ou non de rendre compte des informations disponibles, et c'est exactement ce que se propose de faire la géostatistique  ; mais la réponse n'est pas exclusive, et il est parfaitement envisageable que des modèles fondamentalement contradictoires rendent compte simultanément d'un même phénomène avec la même qualité^[145].

A fortiori, il serait vain de chercher à donner une signification objective à l'espace probabilisé sur lequel est définie la FA : quelle réalité tangible pourrait-on accorder à l'univers dans lequel la VR étudiée aurait été censée prélevée ? et surtout, comment pourrions nous accéder à la loi de probabilité de ce prélèvement, sachant que nous ne disposons que d'un seul résultat (la VR) du dit prélèvement ? Cela dit, même en refusant les spéculations métaphysiques sur l'espace probabilisé, nous ne pourrons esquiver la question méthodologique qui sous-tend toute la démarche de la géostatistique intrinsèque : comment peut-on justifier l'emploi de modèles probabilistes pour rendre compte d'un phénomène unique ? La réponse est apportée progressivement, dans les étapes successives de mise en place du formalisme intrinsèque ; on peut aussi noter que cette interrogation constitue en filigrane le sujet principal de Estimer et choisir, qui en examine tous les aspects et toutes les implications.

Il est clair en tout cas que le recours à une modélisation probabiliste développe des outils plus abstraits que ne le faisait le traitement direct de la VR, et que par suite les risques de perdre le contact avec la réalité et de dépasser le seuil de réalisme sont considérablement accrus. Cette prise de risque ne se justifie que par l'efficacité de ce nouveau niveau d'abstraction, efficacité constatée par toutes les études et tous les développements entrepris depuis les débuts de la géostatistique appliquée. Fondamentalement, les précautions méthodologiques à prendre sont exactement celles qui ont été évoquées à propos du modèle primaire et donc, bien qu'elles soient ici plus cruciales, il n'y a pas lieu de les répéter. Paradoxalement, alors qu'il existait encore un risque réel de confusion au niveau du modèle primaire tant la VR pouvait facilement être confondue avec le phénomène^[146], le danger de confusion est ici minime : personne n'a jamais observé d'espace probabilisé, personne n'a jamais touché une loi de probabilités. Ces êtres mathématiques, dont on attend beaucoup au niveau des constructions théoriques, ne sont en aucun cas des grandeurs régionales : ce sont des purs artefacts, des produits de notre intellect. Il est donc clair que les éléments de l'espace probabilisé doivent impérativement être évincés du résultat final si celui-ci prétend pouvoir être associé à une propriété physique^[147], contrôlable « sur le terrain » : la phase de reconstruction opératoire est ici cruciale si l'on veut simplement que les conclusions d'une étude ait une signification concrète.

Conventions d'écriture

Un espace probabilisé est usuellement représenté par un triplet

où :

• l'ensemble Ω désigne un univers ;
• l'ensemble est un ensemble de parties de Ω, muni d'une structure de tribu (donc, en particulier, ). Les éléments de Ω sont appelés évènements ;
• le couple constitue par définition un espace probabilisable ;
• P , appelée probabilité, est une mesure positive définie sur et vérifiant .

Si on désigne comme dans les exemples précédents l'espace de départ (« géographique^[148] ») par D , une fonction aléatoire Z sera définie comme étant une famille de variables aléatoires définies sur l'espace probabilisable et à valeurs dans l'espace d'arrivée, cette famille étant indexée par D. Une notation possible est donc

Toutefois, cette écriture ne met pas assez en lumière le fait que l'ensemble D doit être un espace métrique, et que l'on s'intéresse au premier chef aux propriété structurales de Z considérée comme fonction sur D. Aussi la géostatistique préfère-t-elle noter une fonction aléatoire comme une fonction de deux variables, l'une parcourant l'espace probabilisable et l'autre l'espace « géographique ». De sorte que l'usage sera par exemple de représenter une FA réelle^[149] sous la forme

Cette présentation sous forme d'une fonction de deux variables montre que :

• pour un événement ω₀ fixé dans , l'objet mathématique Z(x,ω₀) est une fonction déterministe d'une seule variable, définie sur l'espace « géographique » D : c'est donc, très exactement, une variable régionalisée. Cette observation va fonder la méthodologie de travail en géostatistique intrinsèque, présentée dans les alinéas suivants ;
• pour un point x₀ fixé dans l'espace « géographique » D, l'objet mathématique Z(x₀,ω) est une fonction d'une seule variable définie sur l'espace probabilisable  : c'est donc une variable aléatoire.

En fait, d'une part parce que l'espace des événement n'a pas de réalité physique (donc, ω non plus), d'autre part parce que c'est principalement la structuration dans l'espace de départ qui intéresse le géostatisticien, on écrit en général la FA comme une fonction d'une seule variable : Z(x) , accentuant ainsi le parallélisme avec la VR associée z(x) . Le caractère aléatoire est, conventionnellement, révélé par l'utilisation d'une lettre majuscule^[150].

Ainsi, lorsque l'on associe une FA Z à une VR z, il sera automatiquement possible d'associer à toute grandeur régionale une version probabiliste qui s'obtiendra en remplaçant dans son expression la VR par la FA ; et, au niveau des écritures, cela reviendra simplement à changer une minuscule en majuscule. Ainsi, en gardant les conventions d'écritures définies précédemment, on a le tableau de correspondances^[151] :

Version VR			Version FA
Statut :	Notation :	Notation :	Statut :
Nombre			Variable aléatoire
Fonction			Fonction aléatoire
Nombre			Variable aléatoire
Nombre			Variable aléatoire
Fonction			Fonction aléatoire
Fonction			Fonction aléatoire

Il reste maintenant à expliciter le mécanisme intellectuel qui règle l'association entre une VR et une FA, puis à décrire comment ce mécanisme intervient dans une étude géostatistique.

Réalisation

D'un point de vue purement mathématique^[152], l'écriture d'une FA^[153] comme étant une fonction de deux variables sur un ensemble abstrait  :

montre comment une fonction aléatoire génère des variables régionalisées : pour chaque événement (élément) ω₀ fixé de la tribu , l'application partielle

devient en effet une fonction d'une seule variable définie sur le seul ensemble géographique . Toute référence à un contexte probabiliste est désormais écartée, de sorte que conformément aux conventions d'écriture, il est légitime de représenter cette fonction par une lettre minuscule. Et cette fonction a très exactement la signification d'une variable régionalisée. Ainsi, lorsqu'on dispose d'une FA , il est possible de construire autant de VR qu'il sera possible de choisir des éléments dans la tribu d'événements sous-jacente.

Cette construction est pour le moment purement algébrique, et ne met en jeu que l'espace probabilisable. L'aspect aléatoire intervient dans la manière de choisir , et ce choix sera tributaire de la loi de probabilité , de sorte que intuitivement^[154] , toutes les VR possibles associées à une même FA n'auront en général pas la même chance d'être tirées au hasard. Le mécanisme complet consistant d'abord à tirer un événement au hasard puis à lui associer la VR correspondante est appelé réalisation du processus (synonyme : de la FA) et par extension, on dira en abrégé que « la VR est une réalisation de la FA  » .

Cette dernière formulation escamote à la fois la tribu et la loi de probabilités  : cela n'est nullement gênant dans la mesure où ces deux concepts mathématiques n'ont strictement aucune existence objective, pour cette raison ne doivent intervenir que le plus discrètement possible dans les développements algorithmiques (principe de parcimonie), et ne doivent pas être présents dans l'énoncé du résultat ultime d'une étude appliquée.

Il convient en revanche d'insister sur le fait que la VR n'est que une — et une seule — réalisation, parmi beaucoup d'autres possibles dans le cadre du modèle probabiliste sous-jacent^[155]. Autrement dit, le modèle FA est beaucoup plus riche et complexe que le modèle VR, et beaucoup plus abstrait également en ceci qu'il dépend de beaucoup de facteurs (tribu d'événement, loi de probabilités) qui n'ont pas de signification objective et ne peuvent donc faire l'objet d'un contrôle expérimental. Sur le plan pratique, il faut prendre conscience de ce que le recours à un modèle probabiliste augmente considérablement les risques de franchir le seuil de réalisme ; et sur le plan épistémologique, il faut s'interroger sur la signification qu'il y a à vouloir représenter un phénomène unique^[156] (la VR, pour faire simple) par un modèle aléatoire : cette problématique, véritablement fondamentale et essentielle^[157], constitue la matière de l'ouvrage de Georges Matheron Estimer et choisir. Quant à la justification du recours à une méthodologie indéniablement plus délicate^[158] à mettre en œuvre que le modèle primaire, elle est de nature empirique : le développement des travaux et outils de la géostatistique depuis le milieu des années 1950 a clairement établi l'intérêt des outils probabilistes en matière d'efficacité, et justifié les complications méthodologiques qu'ils introduisent.

Immersion probabiliste

Lorsqu'un praticien aborde une nouvelle étude, il dispose d'un jeu de valeurs numériques qui constituent un échantillonnage du modèle primaire, c'est-à-dire d'une variable régionalisée. S'il souhaite travailler dans le cadre de la géostatistique intrinsèque, il doit associer cette VR à une fonction aléatoire, sur laquelle les outils théoriques permettront d'établir des résultats bénéficiant de toute l'efficacité des modèles aléatoires. Cette opération est appelée « randomisation », ou plus rarement immersion probabiliste^[159].

Bien que plus fréquent, le mot « randomisation^[160] » ne semble pas opportun, principalement parce qu'il peut prêter à confusion. Il décrit en effet parfois l'action de réaliser des prélévements aléatoires dans un jeu de données, et ce n'est clairement pas de cela qu'il s'agit lorsqu'on passe d'une VR à une FA.

Cependant, dans son acception la plus précise^[161], randomiser une variable aléatoire dépendant d'un paramètre signifie que l'on donne à ce paramètre un statut aléatoire : la variable randomisée devient, en quelque sorte, « doublement aléatoire »... Ce point de vue est, cette fois, transposable à la géostatistique intrinsèque : il consiste à considérer qu'une VR donnée est en réalité une fonction (déterministe) indexée par un certain paramètre , puis à remplacer ce paramètre par une variable aléatoire d'un espace probabilisé . Ainsi, on décide de poser — avec des notations un peu hybrides^[162] :

et on définit la FA associée à la VR par la relation :

Le choix, habituel dans les publications de géostatistique, de ne pas faire figurer la seconde variable () n'est pas un simple allègement de notation. Cela évite d'attirer l'attention sur un paramètre qui n'a aucune réalité physique, et sur lequel le praticien n'a aucun moyen d'action. On écrit donc usuellement une FA , le caractère aléatoire (dans le modèle) de cette fonction étant conventionnellement désigné seulement par l'utilisation d'une lettre majuscule.

En examinant le mécanisme méthodologique qui fait passer des aux , on constate qu'il s'agit bel et bien de plonger une classe d'objets mathématiques déjà fort riche (les VR) dans un ensemble infiniment plus vaste (les FA) : l'expression « immersion probabiliste », bien que peu fréquemment utilisée, paraît donc judicieuse et sera conservée dans la suite de l'article.

Enfin, cette abstraction croissante fait naturellement courir des risques accrus de dépasser le seuil de réalisme, et le géostatisticien se doit d'être particulièrement vigilant. Mais en contrepartie, il bénéficiera de tout l'arsenal des outils et théorèmes de la théorie des probabilités et des processus stochastiques ; et si, au prix éventuel de transformations^[163] , il se limite à manipuler des FA de variance finie, il pourra munir son espace (de FA) d'arrivée d'une structure d'espace de Hilbert qui lui garantira par théorème l'exactitude de ses principaux résultats (interpolation, estimation, filtrage, etc.) : le gain théorique est immense, et justifie pleinement les efforts de rigueur qu'il faut consentir.

En conclusion : méthodologie de la géostatistique intrinsèque

L'animation ci-dessous rappelle de façon allégorique les trois niveaux d'une étude géostatistique. L'image du fond représente un chantier d'orpaillage industriel, pour rappeler qu'une étude de géostatistique appliquée a vocation à répondre à des questions concrètes, avec des enjeux non seulement méthodologiques, mais aussi techniques et économiques.

Animation bloquée...

La première colonne se réfère à la réalité physique, au monde dans lequel le problème à résoudre a été posé. Les enjeux d'une étude peuvent être considérables : implicitement, dans l'illustration proposée, il s'agit d'exploiter un gisement minier. La sanction ultime sera en l'occurrence la rentabilité de l'entreprise : une sanction en général sans ambiguïté, mais qui n'arrive qu'en toute fin du travail. Ainsi, la mission qui est confiée au géostatisticien est essentiellement d'anticiper ce qui sera finalement plus tard une simple constatation — si du moins l'exploitation est réellement entreprise et menée à son terme : il s'agit donc d'aller plus loin que ce disent hic et nunc les données, ce qui ne peut se faire qu'au prix d'un exercice intellectuel de modélisation.

La seconde colonne rappelle que le premier niveau de modélisation consiste à considérer le réel comme une fonction, comme un être mathématique : c'est l'introduction du concept de variable régionalisée. Symboliquement, l'arrière-plan de la figure est ici en partie brouillé, pour rappeler que l'exercice de modélisation nous éloigne partiellement de la réalité, à la fois en ne prenant pas en compte toute la complexité du réel, et en introduisant dans le même temps des propriétés mathématiques qui n'ont peut-être aucune contrepartie dans la réalité. Ce cadre du modèle primaire permet déjà des traitements spécifiques (statistiques) et constitue la matière de la géostatistique transitive.

Le passage à la troisième colonne constitue la caractéristique de la géostatistique intrinsèque : il consiste, sur la base de la seule variable régionalisée dont nous disposons, à invoquer une fonction aléatoire dont la VR serait une réalisation parmi une infinité d'autres. C'est le processus fondamental de l'immersion probabiliste qui, symboliquement, revient à remplacer z par Z . Nous sommes ici dans un niveau d'abstraction bien plus élevé, c'est pourquoi symboliquement l'arrière-plan n'est presque plus discernable ; c'est pourquoi aussi le risque d'entreprendre des développements théoriques ne correspondant à rien dans la réalité est considérablement accru. Mais dans le même temps, on bénéficie de toute la richesse des outils probabilistes qui permettent de formaliser le problème initial en termes théoriques, et d'en proposer une solution.

L'étude ne doit pas s'arrêter là. Il convient maintenant d'exprimer la réponse théorique en termes concrets. Il faut donc d'abord veiller à ce que cette réponse ne soit tributaire d'aucun paramètre conventionnel, et puisse ne s'exprimer qu'en termes de grandeurs régionales. Ensuite, dans l'expression de la solution théorique, il faut remplacer la fonction aléatoire par la variable régionalisée (remplacer Z par z) : c'est la phase de réalisation, qui est à la base de la reconstruction opératoire. Le résultat fourni alors a vocation à être comparé à la réalité.

Pour conclure l'interprétation de cette figure, il faut remarquer que l'utilisateur ne dispose d'aucun degré de liberté dans la colonne de gauche, puisque la réalité s'impose à tous indépendamment de tous choix méthodologiques et de toutes préférences subjectives ; et inversement, plus on avance dans l'abstraction et plus on dispose de possibilités de faire des choix arbitraires et subjectifs. Aussi, s'il arrive qu'à l'issue d'un travail les résultats proposés se révèlent incompatibles avec les mesures de contrôle, c'est bien sûr au niveau des modèles qu'il convient d'apporter des corrections. Il faut alors entreprendre un nouveau cycle : éventuellement un nouveau modèle primaire, assurément une nouvelle immersion probabiliste, refaire exécuter les algorithmes et réeffectuer la reconstruction opératoire ; l'essentiel est de garder à l'esprit que, en cas de conflit entre la réalité et le modèle, c'est le modèle qui doit s'aligner sur la réalité...

Notes et compléments

Index

Cet index répertorie les principaux mots-clefs rencontrés dans le corps de cet article, et renvoie à l'emplacement où ils ont été définis ou employés pour la première fois (mots ou expressions qui, conformément à la convention typographique, sont écrits en caractères gras lors de leur première utilisation).

• Analyse krigeante ↑
• Borne (mathématiques) ↑
• Champ (mathématique) ↑
• Champ (physique) ↑
• Conditionnement ↑
• Contraintes amont ↑
• Contraintes aval ↑
• Distance ↑
• Échelle de travail ↑
• Émergence ↑
• Erreur radicale ↑
• Extrapolation méthodologique ↑
• Extrapolation physique ↑
• Fonction aléatoire, FA ↑
• Géostatistique ↑
• Grandeur régionale ↑
• Hypothèse anticipatrice ↑
• Immersion probabiliste ↑
• Krigeage simple ↑
• Modèle mathématique, modélisation ↑
• Modèle primaire ↑
• Réalisation ↑
• Régularisation ↑
• Variable régionalisée, VR ↑
• Variogramme, variographie ↑
• Version probabiliste d'une variable régionalisée ↑

Voir aussi, dans la boîte déroulante « Définitions possibles de la géostatistique » (↑) :

• Analyse structurale, analyse variographique ↑
• Régionalisation ↑

et dans la boîte « Commentaires et éléments pour une réflexion personnelle » (↓) :

• Analyse objective ↑
• Géostatistique transitive ↑
• Phénomènes de transition ↑
• Reconstruction opératoire ↑
• Seuil d'objectivité ↑

Notes

Compléments et ouvertures

Bibliographie

Ouvrages

Il s'agit d'une liste, nécessairement incomplète, se limitant aux ouvrages de synthèse (cours ou manuels) et classée par ordre chronologique de publications.

• (fr) Georges Matheron, Traité de géostatistique appliquée, tomes 1 & 2, Éditions Technip, Paris, 1962 ; tome 3, Éditions du B.R.G.M., Paris, 1962.
• (en) Georges Matheron, Principles of geostatistics, Economic Geology vol. 58, 1963.
• (fr) Georges Matheron, Les variables régionalisées et leur estimation, Masson, Paris, 1965.
• (fr) Jean Serra, Échantillonnage et estimation locale des phénomènes de transition miniers, Thèse de docteur-ingénieur, Université de Nancy, 1967.
• (ru) Georges Matheron, Osnovy prikladnoï geostatistiki, Éditions Mir, Moscou, 1968.
• (en) Daniel F. Merriam, Geostatistics, Plenum Press, New York, 1970.
• (fr) Pierre Laffitte (ed.), Traité d'informatique géologique, Masson, Paris, 1972. Article Théorie des variables régionalisées par Georges Matheron, pp 306-378.
• (en) Georges Matheron, The intrinsic random functions and their applications, Advances in applied probability vol. 5, 1973.
• (en) Michel David, Geostatistical Ore Reserve Estimation, Elsevier Scientific Publishing Company, Amsterdam, 1977.
• (en) André Journel & Charles Huijbregts, Mining Geostatistics, Academic Press Inc., London, 1978.
• (en) Isobel Clark, Practical Geostatistics, Applied Science Publishers, London, 1979.
• (en) Bertil Matérn, Spatial variations, Springer, Berlin, 1986.
• (en) Georges Matheron, Estimating and choosing, Springer, Berlin, 1989. Achevée dès 1978, prévue pour 1980 chez Gauthier-Villars, Paris, sous le titre : Estimer et choisir. Essai sur la pratique des probabilités, l'édition originale en français n'a finalement pas été publiée ; mais il est possible, auprès de la Bibliothèque de Mines ParisTech, d'en obtenir une version sous forme d'une note interne :

  ——> (fr) Georges Matheron, Estimer et choisir, Les Cahiers du Centre de Morphologie Mathématique n°7, École des mines de Paris, 1978.

• (de) Rudolf Dutter, Mathematische Methoden in der Technik, Bd. 2: Geostatistik., B.G. Teubner Verlag, Stuttgart, 1985.
• (en) Noel Cressie, Statistics for spatial data, Wiley Interscience, New York, 1993.
• (en) Jean-Paul Chiles & Pierre Delfiner, Geostatistics: modeling spatial uncertainty, John Wiley & Sons, New York, 1999).
• (en) Christian Lantuéjoul, Geostatistical simulation : models and algorithms, Springer-Verlag, Berlin, 2002.
• (en) Hans Wackernagel, Multivariate Geostatistics, Springer-Verlag, Berlin, 2003.
• (fr) Pierre Chauvet, Aide-mémoire de géostatistique linéaire, Mines ParisTech Les Presses, Paris, 2008. (ISBN 9782911762949)

Actes des Congrès Internationaux de Géostatistique

• (en) Massimo Guarascio, Michel David et Charles Huijbregts (ed.), Advanced Geostatistics in the mining industry, Reidel, Dordrecht, 1976. (ISBN 90-277-0669-7)
• (en) George Verly, Michel David, André Journel et Alain Maréchal (ed.), Geostatistics for natural resources characterization (2 vol.), Reidel, Dordrecht, 1984. (ISBN 90-277-1746-X) et (ISBN 90-277-1747-8)
• (en) Margaret Armstrong (ed.), Geostatistics (2 vol.), Kluwer, Dordrecht, 1989. (ISBN 0-7923-0204-4)
• (en) Amilcar Soares (ed.), Geostatistics Troia'92 (2 vol.), Kluwer, Dordrecht, 1993. (ISBN 0-7923-2157-X)

Voir aussi les actes du forum international à la mémoire de Michel David, Montréal, 1993 :

• (en) Roussos Dimitrakopoulos (ed.), Geostatistics for the next century, Kluwer, Dordrecht, 1994. (ISBN 0-7923-2650-4)

Pages non francophones sur la géostatistique

• (de) Geostatistik. Il existe une catégorie « Geostatistik » sur le Wikipédia allemand.
• (en) Geostatistics. Il existe une catégorie « Geostatistics » sur le Wikipédia anglais.
• (es) Krigeaje (la page Geoestadística est absente sur le Wikipédia espagnol, bien qu'il existe une catégorie « Geoestadística  »).
• (it) Geostatistica. Il existe une catégorie « Geostatistica » sur le Wikipédia italien.
• (pt) Geoestatística. Il existe une catégorie « Geoestatística  » sur le Wikipédia portugais.

Cours en ligne

• (fr) Jean-Stéphane Bailly, Géostatistique appliquée, Agro ParisTech.

Corrélats

• Épistémologie ;
• Espace métrique ;
• Fonction mathématique ;
• Georges Matheron ;
• Gaston Bachelard ;
• Géostatistique intrinsèque ;
• Karl Popper ;
• Modèle mathématique ;
• Rasoir d'Ockham ;
• Statistique descriptive ;
• Théorie de la connaissance ;
• Positivisme logique.

• Portail des mathématiques
• Portail des probabilités et des statistiques
• Portail de l’information géographique