Fonction multivaluée

Fonction multivaluée
Ce diagramme représente une multifonction : à chaque élément de X on fait correspondre une partie de Y ; ainsi à l'élément 3 de X correspond la partie de Y formée des deux points b et c.

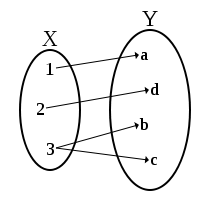
En mathématiques, une fonction multivaluée (aussi appelée fonction multiforme, fonction multivoque ou simplement multifonction) est une relation qui à un élément d'un ensemble associe un ou plusieurs éléments d'un second ensemble. On peut donc voir une multifonction comme une fonction classique prenant ses valeurs dans l'ensemble des parties du second ensemble, même si ce n'est pas nécessairement le point de vue le plus fructueux. Par contraste, si l'image de chaque point est un singleton, on dit que l'application est univoque.

Un exemple simple de fonction multivaluée est la fonction réciproque d'une application non injective : à tout point dans son image on fait correspondre l'image réciproque formée des antécédents de ce point.

Les fonctions multivaluées apparaissent en analyse complexe où l'on peut en considérer des déterminations, c'est-à-dire des restrictions sur ces relations qui en font des fonctions et qui permettent de calculer certaines intégrales réelles par le biais du théorème des résidus comme ce sera illustré plus bas ; l'utilisation en est cependant malaisée et a été remplacée par la considération plus abstraite de fonctions (univaluées) sur des surfaces de Riemann.

Les multifonctions se rencontrent également en analyse convexe et non lisse : les cônes tangent et normal à un ensemble, le sous-différentiel d'une fonction sont des multifonctions. Cette observation et d'autres ont donné une nouvelle impulsion au développement de l'analyse multifonctionnelle (voir la bibliographie).

Sommaire

Exemples

La racine carrée

Article détaillé : racine carrée.
Article détaillé : racine d'un nombre complexe.
  • Dans les réels, à chaque élément positif x, la relation "racine carrée" fait correspondre deux éléments | y | et − | y | avec | y | 2 = x. On se restreint de manière habituelle à la valeur positive | y | pour avoir alors la fonction racine carrée.
  • Dans les complexes, en définissant un élément z du plan complexe \mathbb C par z = | z | eiθ avec θ l'argument de z, les racines carrées de z sont les nombres wk (k\in\mathbb Z) donnés par :
w_k = \sqrt{|z|}\mathrm{e}^{i\theta/2}\mathrm{e}^{i\pi k}
on vérifie en effet que w_k^2 = |z|\mathrm{e}^{i\theta} \mathrm{e}^{2i\pi k} = z puisque e2iπk vaut l'unité pour tout entier k.

Le logarithme complexe

Article détaillé : logarithme complexe.

En définissant un élément z du plan complexe comme précédemment, le logarithme complexe de z sont les nombres wk (k\in \mathbb Z) donnés par :

wk = ln  | z | + iθ + 2iπk

on vérifie en effet que exp(wk) = | z | eiθe2iπk = z puisque, comme précédemment, e2iπk vaut l'unité pour tout entier k.

Définitions

Multifonction

Soient X et Y deux ensembles. Une application multivoque ou simplement multifonction F:X\multimap Y est une application qui à un élément x\in X fait correspondre une partie F(x) de Y. Il s'agit donc d'une fonction de X dans \mathcal{P}(Y), l'ensemble des parties de Y.

Ce n'est cependant pas le point de vue de fonction à valeurs dans \mathcal{P}(Y) qui prime dans certaines définitions. Ainsi, on appelle graphe de F la partie de X\times Y, et non pas de X\times \mathcal{P}(Y), suivante

\mathcal{G}(F):=\{(x,y)\in X\times Y:y\in F(x)\}.

En fait, toute partie G de X\times Y est le graphe de la multifonction F:X\multimap Y définie par F(x):=\{y\in Y:(x,y)\in G\}. Il y a donc une bijection entre les multifonctions F:X\multimap Y et les parties de X\times Y.

Domaine, image, sélection

Le domaine et l'image de F se définissent respectivement par

\mathcal{D}(F)~:=~\{x\in X: F(x)\ne\varnothing\}~=~\pi_X(\mathcal{G}(F))

\mathcal{R}(F)~:=~\{y\in Y: \exists\,x\in X ~\mbox{tel que}~y\in F(x)\}~=~\pi_Y(\mathcal{G}(F)),

où \pi_X:X\times Y\to X:(x,y)\mapsto x et \pi_Y:X\times Y\to Y:(x,y)\mapsto y sont les projections canoniques sur X et Y.

L'image d'une partie P\subset X est définie par

F(P):=\bigcup_{x\in P} F(x)=\{y\in Y:F^{-1}(y)\cap P\ne\varnothing\}.

Clairement, \mathcal{R}(F)=F(X).

Une sélection de F est une fonction f:\mathcal{D}(F)\to Y telle que, pour tout x\in\mathcal{D}(F), on a f(x)\in F(x).

Multifonction réciproque

La multifonction réciproque F^{-1}:Y\multimap X de la multifonction F:X\multimap Y est définie en y\in Y par

F^{-1}(y)=\{x\in X:y\in F(x)\}.

Pour x\in X et y\in Y, on a

y\in F(x) \quad\Longleftrightarrow\quad x\in F^{-1}(y),

ce qui s'exprime aussi par

(x,y)\in\mathcal{G}(F) \quad\Longleftrightarrow\quad (y,x)\in\mathcal{G}(F^{-1}).

Ceci permet de voir que

\mathcal{D}(F^{-1})=\mathcal{R}(F), \quad \mathcal{D}(F)=\mathcal{R}(F^{-1})

et pour une partie Q\subset Y :

F^{-1}(Q):= \bigcup_{y\in Q} F^{-1}(y)=\{x\in X:F(x)\cap Q\ne\varnothing\}.

Analyse multifonctionnelle

L'analyse multifonctionnelle s'intéresse à l'étude des multifonctions, à leur semi-continuité et continuité, à leur caractère borné, à leur lipschitzianité, aux multifonctions polyédriques, à la recherche de leurs zéros (des points qui contiennent zéro dans leur image), etc.

Certaines propriétés se définissent naturellement pour des multifonctions, comme la monotonie, l'accrétivité, etc.

Déterminations

Pour la racine carrée complexe et le logarithme complexe, on appelle détermination une restriction sur l'argument θ de la valeur correspondante. Plus explicitement, une détermination pour la racine carrée est donnée par :

\sqrt{z} = \sqrt{|z|}\mathrm{e}^{i\theta/2}, \quad (\theta \in [\theta_0, \theta_0+2\pi[)

avec θ0 un angle quelconque caractérisant la détermination.

De même, une détermination pour le logarithme complexe est donnée par :

\log{z} = \ln{|z|} + i\theta, \quad (\theta \in [\theta_0, \theta_0+2\pi[)

On appelle détermination principale du logarithme la restriction de l'argument à l'intervalle semi-ouvert [ − π,π[.

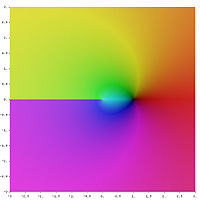
Remarquons que, à une détermination près, la fonction racine carrée complexe et le logarithme complexe sont des fonctions holomorphes sur tout le plan complexe excepté la demi-droite partant de l'origine et d'angle θ0 par rapport à l'axe des abscisses. Dans le cas de la détermination principale, les deux fonctions sont holomorphes sur \mathbb C\backslash]-\infty, 0] . La discontinuité sur l'axe réel négatif est illustrée sur les deux figures ci-dessous.

  • Détermination principale

  • Figure 1 : illustration de la détermination principale du logarithme complexe.

  • Figure 2 : illustration de la détermination principale de la racine carrée complexe.

Application au calcul d'intégrales réelles

Considérer une détermination particulière permet, en s'aidant du théorème des résidus, de calculer certaines intégrales réelles qu'il serait autrement ardu de calculer.

Remarque : la relation suivante est souvent utilisée comme ce sera illustré dans l'exemple ci-dessous : zα = eαlog(z).

Exemple avec le logarithme complexe

Figure 3 : Illustration du contour γ (en bleu) employé pour le premier exemple. Les deux pôles simples \pm i sont représentés en rouge. La partie γR représente le cercle extérieur de rayon R, la partie \gamma_\epsilon représente le demi-cercle intérieur de rayon \epsilon. γ1,2 sont les deux segments restants.

Problème : calculer l'intégrale suivante :

I = \int_0^{+\infty} {x^a\over 1+x^2}\mathrm{d}x

pour | a | < 1.

Solution : En considérant le contour γ illustré à la figure 3 ainsi que la détermination suivante du logarithme :

\mathrm{log}(z) = \ln|z| + i\theta, \quad (\theta\in[0, 2\pi[)

(le contour "entoure" donc la discontinuité de la détermination que nous avons choisie), on obtient : pour 0 < | a | < 1 : I = {\pi\left(\sin(a\pi/2)+\sin(3a\pi/2)\right)\over \sin(a\pi/2)} et pour a = 0, l'intégrale vaut π.

Développement

La fonction f définie par f(z) = {z^a\over 1+z^2} a deux pôles simples (z_{1,2}=\pm i ) tous deux d'indice +1 par rapport à γ (pour \epsilon<1 et R > 1). A la limite \epsilon\to 0 et R\to \infty, le théorème des résidus nous donne donc :

I^* = \int_\gamma f(z) \mathrm{d}z = 2i\pi \left(\mathrm{Res}(f, +i) + \mathrm{Res}(f, -i)\right).

En décomposant l'intégrale curviligne en ses quatre parties principales et en appliquant le lemme d'estimation pour montrer que l'intégrale le long de γε et celle le long de γR tendent vers zéro à la limite, il nous reste :

I^* = \lim_{\epsilon\to 0, R\to \infty} \left(\int_{\gamma_1}f(z)\mathrm{d}z+\int_{\gamma_2}f(z)\mathrm{d}z\right) .

En utilisant la détermination choisie ci-dessus, on a que :

za = ealog(z) = ea(ln  | z | + iθ) = | z | aeaiθ

à la limite \epsilon\to 0, le long du chemin γ1, l'argument θ tend vers zéro ; le long du chemin γ2, l'argument tend vers 2π, on a donc :

\lim_{\epsilon\to 0, R\to \infty}\int_{\gamma_1} {|z|^a\mathrm{e}^{ai\theta}\over 1+z^2}\mathrm{d}z = \int_0^{+\infty}{x^a\over 1+x^2}\mathrm{d}x

et

\lim_{\epsilon\to 0, R\to \infty}\int_{\gamma_2} {|z|^a\mathrm{e}^{ai\theta}\over 1+z^2}\mathrm{d}z = \int_{+\infty}^{0}{x^a\mathrm{e}^{2a i\pi}\over 1+x^2}\mathrm{d}x = - \int_0^{+\infty}{x^a \cos(a\pi/2) \over 1+x^2}\mathrm{d}x- i\int_0^{+\infty}{x^a \sin(a\pi/2) \over 1+x^2}\mathrm{d}x

où l'on a utilisé la formule de Moivre dans la dernière égalité. On a donc :

\Re(I^*) = I(1-\cos(a\pi/1)) ou \Im(I^*) = I(\sin(a\pi/2))

il nous reste à calculer I * via les résidus de la fonction en \pm i :

\mathrm{Res}(f, +i) = \lim_{z\to +i} (z - i)f(z) = {i^{a}\over 2i} = {\mathrm{e}^{ai\pi/2}\over 2i}

et

\mathrm{Res}(f, -i) = {-\mathrm{e}^{3ai\pi/2}\over 2i}

où l'on a utilisé que, dans la détermination choisie, l'argument de + i (resp. − i) est π / 2 (resp. 3π / 2). On obtient donc :

I^* = \pi\left({\mathrm{e}^{ai\pi/2}}-\mathrm{e}^{-3ai\pi/2}\right) = \pi\left(\cos(a\pi/2)-\cos(3a\pi/2)\right) + i\pi\left(\sin(a\pi/2)+\sin(3a\pi/2)\right)

et finalement pour 0 < | a | < 1 :

I = { \pi\left(\cos(a\pi/2)-\cos(3a\pi/2)\right) \over (1-\cos(a\pi/2)} = {\pi\left(\sin(a\pi/2)+\sin(3a\pi/2)\right)\over \sin(a\pi/2)}
où l'on a utilisé la partie réelle de I * pour la première égalité et la partie imaginaire pour la seconde. Pour a = 0, l'intégrale est connue et vaut π, résultat que l'on retrouve par ailleurs en passant à la limite pour chacune des deux expressions possibles données ci-dessus.
 

Exemple avec la racine carrée complexe

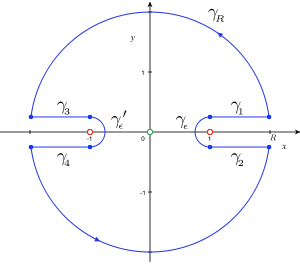Figure 4 : Illustration du contour γ (en bleu) employé pour le second exemple. Les deux points de branchement \pm 1 sont représentés en rouge. Le pôle simple restant (l'origine) est représenté en vert. γR représente le cercle extérieur de rayon R, \gamma_\epsilon et son homologue représentent les demi-cercles intérieurs de rayon \epsilon, les γi sont les segments restants.

Problème : calculer l'intégrale suivante par la méthode des résidus :

I = \int_{1}^{+\infty} {\mathrm{d}x\over x\sqrt{x^2-1}}

(la fonction est uniformisée par la coupure le long de l'axe réel reliant -\infty à -1 et 1 à +\infty.)

Solution : l'intégrande a une primitive (à savoir -\mathrm{atan}\left[\left(x^2-1\right)^{-1/2}\right] ) et on a donc immédiatement I = {\pi\over 2} . On obtient ce même résultat en considérant le contour γ illustré à la figure 4 ci-contre et en utilisant :

\sqrt{z^2-1} = \sqrt{z-1}\sqrt{z+1}

Pour le premier terme du produit, on considèrera la détermination suivante :

\sqrt{z-1} = \sqrt{|z-1|}\mathrm{e}^{i\theta_1/2},\quad \theta_1 \in [0, 2\pi[ ,

pour l'autre, on considérera la détermination principale :

\sqrt{z+1} = \sqrt{|z+1|}\mathrm{e}^{i\theta_2/2},\quad \theta_2\in [-\pi, \pi[.

sous ces déterminations, la fonction est holomorphe sur \mathbb C\backslash \left(]-\infty, -1]\cup[+1, \infty[\right) .

Développement

La fonction f définie par f(z) = {1\over z\sqrt{z^2-1}} a trois singularités[1] : les deux points de branchement (\pm 1) et le pôle simple (l'origine) qui est la seule singularité d'indice non nul par rapport au contour ; à la limite \epsilon\to 0 et R\to \infty, le théorème des résidus nous donne donc :

I^* = \int_\gamma f(z)\mathrm{d}z = 2i\pi\mathrm{Res}(f, 0)~

et \mathrm{Res}(f, 0) = \lim_{z\to 0} z\cdot f(z) = {1\over i} , on a donc I * = 2π.

En décomposant l'intégrale curviligne en ses sept parties principales et en appliquant le lemme d'estimation pour montrer que l'intégrale le long de \gamma_\epsilon, \gamma_\epsilon' et γR tendent vers zéro à la limite, il nous reste :

I^* = \lim_{\epsilon\to 0, R\to\infty} \left(\sum_{i=1}^4 \int_{\gamma_i}f(z)\mathrm{d}z\right)

à la limite \epsilon\to 0, le long du chemin γ1, l'argument θ tend vers zéro pour les deux déterminations, le long du chemin γ2, l'argument tend vers 2π (resp. zéro) pour la première détermination (resp. la détermination principale), le long du chemin γ3 l'argument tend vers π pour les deux déterminations et pour γ4, l'argument tend vers π (resp. − π) pour la première détermination (resp. la détermination principale).

On a donc en notant symboliquement θ1 (resp. θ2) l'argument dans la première détermination (resp. la détermination principale) :

\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_1} {\mathrm{d}z\over z\sqrt{|z-1|}\mathrm{e}^{i\theta_1/2}\sqrt{|z+1|}\mathrm{e}^{i\theta_2/2}}= \int_1^{+\infty}{\mathrm{d}x\over x\sqrt{(x^2-1)}} = I

avec θ1 = θ2 = 0 pour la partie γ1. On a de même :

\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_2} f(z)\mathrm{d}z = \int_1^{+\infty} {\mathrm{d}x\over x\sqrt{(x^2-1)}} = -\int_{+\infty}^0 {\mathrm{d}x\over x\sqrt{x^2-1}} = I

avec θ1 = 2π, θ2 = 0 et eiπ = − 1. Finalement on a aussi :

\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_3} f(z)\mathrm{d}z = -\int_0^{-\infty}{\mathrm{d}x\over x\sqrt{(x^2-1)}} = I
\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_4} f(z)\mathrm{d}z = \int_{-\infty}^{0}{\mathrm{d}x\over x\sqrt{(x^2-1)}} = I

où on a utilisé dans les deux égalités précédentes que la fonction est paire et que l'intégrale sur ]-\infty, 1] est égale à l'intégrale sur [1, \infty[.

On a donc : 4I = I * et finalement, I = {\pi\over 2} ainsi que prévu.
 

Surfaces de Riemann

Article détaillé : surface de Riemann.
Surface de Riemann associée à la fonction racine carrée.

La théorie peu opérante des fonctions multivaluées pour les fonctions de la variable complexe est remplacée dans les mathématiques modernes par le concept plus abstrait de fonction (univaluée) définie sur une surface de Riemann.

Ce point de vue consiste à considérer le domaine de définition d'une fonction multivaluée comme un objet plus élaboré que le plan complexe : une variété complexe de dimension 1.

Annexes

Notes

  1. ↑ on parle ici de singularité au sens large du terme (et donc pas uniquement d'une singularité isolée) c'est-à-dire que la fonction n'est pas analytique en la singularité mais que n'importe quel voisinage ouvert non vide de la singularité contient au moins un point pour lequel la fonction est analytique. [MATHEWS, HOWELL - p.232]

Voir aussi

Bibliographie

  • (en) J.-P. Aubin, Arrigo Cellina (1984). Differential Inclusions, Set-Valued Maps And Viability Theory. Grundlehren der mathematischen Wissenschaften, vol. 264, Springer Verlag, Berlin.
  • (en) J.-P. Aubin, H. Frankowska (1990). Set-Valued Analysis, Birkhäuser, Basel.
  • (en) John H. Mathews, Russel W. Howell (1997). Complex Analysis for Mathematics and Engineering, 3d edition. Jones and Bartlett Publishers International. (ISBN 0-7637-0270-6)
  • (en) R.T. Rockafellar, R. Wets (1998). Variational Analysis. Grundlehren der mathematischen Wissenschaften, vol. 317, Springer.
  • Murray R. Spiegel (1973). Variables Complexes. Schaum, (ISBN 2-7042-0020-3)

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction multivaluée de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Fonction multiforme — Fonction multivaluée Ce diagramme ne représente pas une vraie fonction car à l élément 3 appartenant à X correspond deux éléments dans Y : b et c. En mathématiques, une fonction multivaluée (aussi appelée multiforme) est une fonction qui… …   Wikipédia en Français

  • Fonction (mathématique) — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction …   Wikipédia en Français

  • Fonction Réelle — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction …   Wikipédia en Français

  • Fonction et application — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction …   Wikipédia en Français

  • Fonction mathématique — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction …   Wikipédia en Français

  • Fonction réciproque — Application réciproque Pour les articles homonymes, voir Réciproque (homonymie). En mathématiques, une application réciproque est en des termes simples une fonction qui « fait exactement l inverse de ce que fait une application donnée » …   Wikipédia en Français

  • Fonction réelle — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction …   Wikipédia en Français

  • Logarithme complexe — Courbe de densité représentant la branche principale de la fonction logarithme complexe. En mathématiques, le logarithme complexe est une fonction généralisant la fonction logarithme naturel (définie sur ) au domaine des nombres comple …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”