Problème mal posé

Problème mal posé

Problème bien posé

Le terme mathématique de problème bien posé provient d'une définition de Hadamard. Il pensait que les modèles mathématiques de phénomènes physiques devraient avoir les propriétés suivantes :

  1. Une solution existe
  2. La solution est unique
  3. La solution dépend de façon continue des données, pour une topologie raisonnable.

Exemples

Le problème de Dirichlet pour l'équation de Laplace et l'équation de la chaleur avec des conditions initiales spécifiées. Ils peuvent être considérés comme des problèmes « naturels », dans le sens où il y a des processus physiques qui résolvent ces problèmes.

Au contraire, l'équation inversée de la chaleur, par laquelle on déduit une distribution passée de la température à partir des données finales, n'est pas bien posée puisque la solution est très sensible à des changements dans les données finales. Il est fréquent que les problèmes inverses ne soient pas bien posés. De tels problèmes de continuum doivent souvent être résolus de façon discrète (« discrétisés ») si l'on veut obtenir une solution numérique. Bien qu'en termes d'analyse fonctionnelle, ces problèmes soient typiquement continus, il peuvent s'avérer instables lorsqu'ils sont résolus avec une précision finie, ou avec des erreurs dans les données.

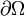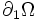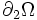En mécanique des milieux continus un problème bien posé est un problème dans lequel le bord \partial\Omega du milieu considéré admet une partition en deux ensembles \partial_1\Omega et \partial_2\Omega tels que sur le premier il n'y ait que des déplacements imposés et sur le second uniquement des efforts.

Si un problème de mécanique est bien posé, alors la solution en contrainte existe et est unique, mais la solution en déplacement peut ne pas être unique si des mouvements de corps rigides sont possibles.

De plus on peut aussi remarquer que la partition du bord peut se faire suivant les trois direction de l'espace, c’est-à-dire que sur une même partie du bord on peut imposer un déplacement et un effort si ces deux conditions concernent des direction orthogonales de l'espace.

Mesures et solutions

Le nombre conditionnel mesure à quel degré le problème est bien posé, pour les problèmes linéaires discrets.

Si un problème est bien posé, il y a de bonnes chances qu'une solution soit trouvée par un algorithme stable, sur un ordinateur. Sinon, il doit être reformulé pour traitement numérique. Typiquement, cela suppose des hypothèses supplémentaires, par exemple la régularité de la solution. Ce processus est connu sous le nom de régularisation Tychonoff.

Références

  • Jacques Hadamard, Sur les problèmes aux dérivées partielles et leur signification physique, Princeton University Bulletin, 1902, p. 49—52.
  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Probl%C3%A8me bien pos%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Problème mal posé de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Problème bien posé — Le concept mathématique de problème bien posé provient d une définition de Hadamard qui pensait que les modèles mathématiques de phénomènes physiques devraient avoir les propriétés suivantes : Une solution existe La solution est unique La… …   Wikipédia en Français

  • problème — [ prɔblɛm ] n. m. • 1382; lat. problema, du gr. problêma 1 ♦ Question à résoudre qui prête à discussion, dans une science. Problèmes philosophiques, moraux, métaphysiques. Le problème du mal. Soulever un problème. C est là la clé, le nœud du… …   Encyclopédie Universelle

  • Problème numérique — Analyse numérique Simulation numérique d un crash de véhicule L’analyse numérique est une discipline des mathématiques. Elle s’intéresse tant aux fondements théoriques qu’à la mise en pratique des méthodes permettant de résoudre, par des calculs… …   Wikipédia en Français

  • Problème —          ARON (Raymond)     Bio express : Philosophe et sociologue français (1905 1983)     «Le problème politique est éternel que l on retourne la terre à la pioche ou avec le bulldozer.»     Source : Dimension de la conscience historique… …   Dictionnaire des citations politiques

  • Probleme de la mesure quantique — Problème de la mesure quantique Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique H …   Wikipédia en Français

  • Problème de la mesure — quantique Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique H …   Wikipédia en Français

  • Mal — Pour les articles homonymes, voir MAL. « Maux » redirige ici. Pour la commune française, voir Maux (Nièvre). Le mal décrit un certain type d événements, de comportements ou d états de fait jugés nuisibles, destructeurs ou immo …   Wikipédia en Français

  • Problème de la mesure quantique — Le problème de la mesure quantique a été formalisé pour la première fois par John von Neumann en 1932 dans son livre Les Fondements mathématiques de la mécanique quantique (chapitre VI). Il a été par la suite, en 1935, popularisé par Erwin… …   Wikipédia en Français

  • MAL — Le propre du mal tient en ceci qu’il ne peut être nommé, pensé, vécu qu’en relation avec une certaine idée du bien. Qu’il n’y ait pas de bien en soi, que ce que les hommes appellent le bien soit relatif aux situations et aux cultures, et le mal… …   Encyclopédie Universelle

  • Probleme de Monty Hall — Problème de Monty Hall Le problème de Monty Hall est un casse tête probabiliste librement inspiré du jeu télévisé américain Let s Make a Deal [1]. Il est simple dans son énoncé mais non intuitif dans sa résolution et c est pourquoi on parle… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”