- Graphe simple
-
Pour les articles homonymes, voir Graphe.On pourra se reporter à la page Théorie des graphes pour une définition du concept général de graphe, pour une explication du vocabulaire utilisé, et pour une représentation des objets définis ici.
Un graphe est dit simple s'il n'a pas de liens doubles ni de boucles. Dans un graphe simple , s'il existe un arc (pour un graphe orienté, une arête pour un graphe non orienté) du sommet x vers le sommet y, alors il n'existe aucun autre arc de x vers y (mais il peut exister un arc de y vers x si le graphe est orienté), et il n'existe aucun arc (resp. aucune arête) d'un sommet vers lui-même.
Sommaire
Graphe orienté simple
Un graphe simple orienté G est un couple (V,A) où :
- V est appelé l'ensemble des sommets de G, et
est un ensemble de couples d'éléments de V appelé l'ensemble des arcs de G.
La lettre V est utilisée pour les sommets car en anglais, sommet se dit vertex (au pluriel vertices).
Exemple
Un petit graphe orienté
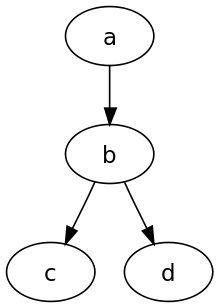
Le schéma ci-contre représente un petit graphe orienté, composé de :
- 4 sommets V = {a,b,c,d}
- 3 arcs A = {(a,b),(b,c),(b,d)}
On a (entre autres) :
- Le degré entrant de b: d − (b) = 1
- Le degré sortant de b: d + (b) = 2
Graphe non-orienté simple
Un graphe simple non-orienté G est un couple (V,E) où :
- V est appelé l'ensemble des sommets de G, et
est un ensemble de paires d'éléments de V appelé l'ensemble des arêtes de G.
(Ici
désigne l'ensemble des parties de cardinalité 2 de V.)La lettre E est utilisée pour les arêtes car en anglais, arête se dit edge.
Exemple
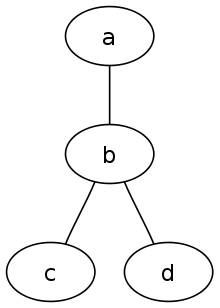
Un petit graphe non-orientéLe schéma ci-contre représente un petit graphe non-orienté, composé de :
- 4 sommets V = {a,b,c,d}
- 3 arêtes E = {{a,b},{b,c},{b,d}}
On a (entre autres) :
- Le degré de b: d(b) = 3
Voir aussi
Catégorie :- Concept en théorie des graphes
Wikimedia Foundation. 2010.
