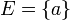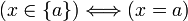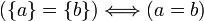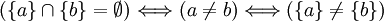Singleton (mathematiques)
- Singleton (mathematiques)
-
Singleton (mathématiques)
En mathématiques, un ensemble E est un singleton lorsqu'il ne contient qu'un seul élément a, et il s'écrit alors :
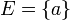
Exemples
- {π} est un singleton de réels.
- {cos} est un singleton de fonctions de variable réelle.
- {{1}} est un singleton d'ensemble d'entiers et ne doit pas être confondu avec {1}, qui lui est un singleton d'entiers.
Propriétés
- Pour tout ensemble E il n'y a qu'une seule fonction de E dans le singleton, ou encore l'ensemble des fonctions de E dans le singleton est un singleton.
Appartenance d'un élément à un singleton
Un élément x appartient à un singleton si et seulement s'il est égal à l'élément de ce singleton ; ce qui s'écrit mathématiquement :
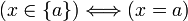
Égalité de deux singletons
Les singletons {a} et {b} sont égaux si et seulement si leurs éléments sont égaux.
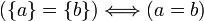
Deux singletons {a} et {b} sont disjoints si et seulement si leurs éléments a et b sont différents, ce qui revient à dire que les singletons disjoints sont les singletons différents.
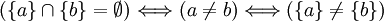
Cardinalité d'un singleton
Le cardinal d'un singleton est 1, puisque par définition il ne contient qu'un seul élément.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie des ensembles
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Singleton (mathematiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Singleton (mathématiques) — Pour les articles homonymes, voir Singleton. En mathématiques, un ensemble E est un singleton lorsqu il ne contient qu un seul élément a, et il s écrit alors : Sommaire … Wikipédia en Français
Singleton — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Singleton peut signifier : Science Singleton dans le domaine de la théorie des ensembles en mathématiques, ensemble ne contenant qu un unique élément … Wikipédia en Français
Paire (mathématiques) — Paire Pour les articles homonymes, voir paire (homonymie). On dit qu un ensemble E est une paire lorsqu il est formé de deux éléments distincts a et b, et il s écrit alors : Quand l ensemble E est formé d un seul élément, a, on dit que E est … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Couple (Mathématiques) — Pour les articles homonymes, voir Couple. En mathématiques, un couple de deux objets est la donnée de ces deux objets dans un ordre déterminé. Le couple des deux objets a et b est noté (a,b). Si a et b sont distincts le couple (a,b) est distinct… … Wikipédia en Français
Doublet (mathématiques) — Couple (mathématiques) Pour les articles homonymes, voir Couple. En mathématiques, un couple de deux objets est la donnée de ces deux objets dans un ordre déterminé. Le couple des deux objets a et b est noté (a,b). Si a et b sont distincts le… … Wikipédia en Français
Graphe de Hoffman-Singleton — Schéma du graphe de Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés … Wikipédia en Français
Couple (mathématiques) — Pour les articles homonymes, voir Couple. En mathématiques, un couple de deux objets est la donnée de ces deux objets dans un ordre déterminé. Le couple des deux objets a et b est noté (a,b). Si a et b sont distincts le couple (a,b) est distinct… … Wikipédia en Français
Graphe singleton — Représentation du graphe singleton. Nombre de sommets 1 Nombre d arêtes 0 Distribution des degrés 0 régulier Rayon 0 … Wikipédia en Français
 Pour les articles homonymes, voir Singleton.
Pour les articles homonymes, voir Singleton.