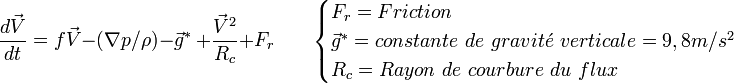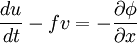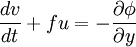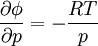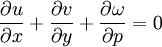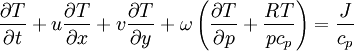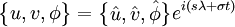Equations primitives atmospheriques

Equations primitives atmospheriques

Équations primitives atmosphériques

Les équations primitives atmosphériques sont une version simplifiée des équations de Navier-Stokes. Elles sont applicables dans le cas d’un fluide à la surface d’une sphère en posant comme hypothèses que la composante verticale du mouvement est beaucoup plus faible que la composante horizontale et que la couche de fluide est très mince relativement au rayon de la sphère. Ces hypothèses correspondent en général au flux à grande échelle, dite échelle synoptique, de l’atmosphère terrestre et ces équations sont donc appliquées en météorologie et en océanographie. Les modèles numériques de prévision du temps résolvent ces équations ou une variante de celles-ci afin de simuler le comportement futur de l’atmosphère.

D’autre part, les équations primitives appliquées à l’océanographie permettent de simuler le comportement des mers. Réduites à une seule dimension, elles résolvent les équations de Laplace de la marée, un problème de valeurs propres duquel on obtient analytiquement la structure latitudinale de la circulation océanique.

Sommaire

Définitions

En général, toutes les formes d’équations primitives relient cinq variables et leur évolution dans le temps[1]:

  • u est la vitesse zonale (direction est/ouest tangente à la sphère).
  • v est la vitesse méridionale (nord/sud).
  • ω est le mouvement vertical
  • T est la température
  • φ est le géopotentiel

Elles utilisent également des variables connues:

Formes diverses des équations primitives

La représentation des équations primitives dépend des coordonnées verticales utilisées. On peut utiliser la pression, le logarithme de la pression ou des coordonnées dites « sigma » qui sont un rapport entre la pression à un niveau et la pression de surface. De plus, la vitesse, la température et le géopotentiel peuvent être décomposés en leur valeur moyenne et leur valeur de perturbation selon la décomposition de Reynolds.

En coordonnées de pression et cartésiennes

Si on utilise la pression comme coordonnées verticale et (x, y) comme coordonnées horizontale tangentielles à la sphère, en négligeant la courbure de la Terre, on obtient une représentation simple des processus physiques en jeu :

  • Le mouvement de l'air ou des mers dans un système en rotation est une balance entre diverses forces : la force de Coriolis, le gradient de pression, la gravité, la force centripète et la friction. Selon le second principe de Newton, on additionne ces forces pour connaître la force totale qui s'exerce sur le fluide:
\frac{d \vec{V}}{dt} = f \vec{V} - (\nabla p/\rho) - \vec g^*\ + \frac {\vec V^2}{R_c} + F_{r} \qquad \begin{cases} F_r = Friction \\ \vec g^*=constante\ de\ gravit\acute{e}\ verticale= 9,8 m/s^2 \\R_c = Rayon\ de\ courbure\ du\ flux \end{cases}
Les équations géostrophiques du mouvement (la pression et force de Coriolis s'opposant) s'obtiennent en négligeant la friction et la force centripète. Comme le mouvement est horizontal 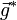\vec g^* est nul étant vertical. Ainsi en changeant pour les coordonnées en géopotentiel φ, on obtient :
\frac{du}{dt} - f v = -\frac{\partial \phi}{\partial x}
\frac{dv}{dt} + f u = -\frac{\partial \phi}{\partial y}
  • L’équation de l'équilibre hydrostatique pour le cas spécial du mouvement vertical dans lequel il n’y a pas d’accélération:
\frac{\partial \phi}{\partial p} = - \frac{R T}{p}
  • L’équation de continuïté qui connecte la convergence/divergence de masse horizontale avec le mouvement vertical (aucune création/perte de masse juste changement de niveau) :
\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial \omega}{\partial p} = 0
\frac{\partial T}{\partial t} + u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} + \omega \left( \frac{\partial T}{\partial p} + \frac{R T}{p c_p} \right) = \frac{J}{c_p}

En ajoutant une équation de composition qui relie le contenu en eau de l'air (ou de sel dans la mer) et sa variation dans l'espace on obtient un ensemble de variables qui décrivent le comportement de l’atmosphère (mer).

En coordonnées sigma et projection polaire stéréographique

Si on divise l’atmosphère non pas en pression absolue mais en niveaux ayant un même rapport avec la pression de surface, on parle de coordonnées sigma. Par exemple, si on divise la couche atmosphérique en trois niveaux: surface, niveau ou la pression est la moitié de celle au sol et sommet de l’atmosphère (pression nulle); on aurait sigma = 1, sigma = 0,5 et sigma = 0.

D’autre part, la projection polaire stéréographique[2] peut être représentée à l'aide d'un plan qu’on pose sur un pôle et sur lequel on projette le contour des continents comme si une lumière illuminait le globe depuis le centre de la Terre. On obtient comme résultat une projection cartographique plane. Cette projection peut être considérée comme une vue de la Terre au-dessus du pôle nord. Cette projection convient aux domaines situés au voisinage de la latitude 60 degrés nord. Elle est valide jusqu'au pôle nord mais elle n'est pas recommandée pour des régions proches de l'équateur car les déformations augmentent d'une manière importante dès qu'on s'en approche.

En utilisant ces deux types de coordonnées, on peut simplifier les équations primitives[3] ainsi:

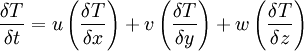
  • Température: \frac {\delta T}{\delta t} = u \left( \frac{\delta T}{\delta x}\right) + v \left( \frac{\delta T}{\delta y}\right) + w \left( \frac{\delta T}{\delta z}\right)
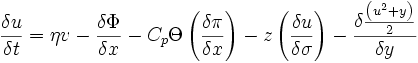
  • Vent u: \frac{\delta u}{\delta t} = \eta v - \frac {\delta \Phi}{\delta x} - C_p \Theta \left( \frac{\delta \pi}{\delta x}\right) - z \left( \frac{\delta u}{\delta \sigma}\right) - \frac {\delta \frac {\left(u^2 +y \right)}{2}}{\delta y}
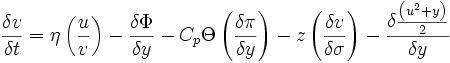
  • Vent v: \frac{\delta v}{\delta t} = \eta \left( \frac {u}{v} \right) - \frac {\delta \Phi}{\delta y} - C_p \Theta \left( \frac{\delta \pi}{\delta y}\right) - z \left( \frac{\delta v}{\delta \sigma}\right) - \frac {\delta \frac {\left(u^2 +y \right)}{2}}{\delta y}
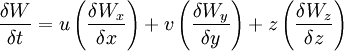
  • Contenu en eau: \frac {\delta W}{\delta t} = u \left( \frac{\delta W_x}{\delta x}\right) + v \left( \frac{\delta W_y}{\delta y}\right) + z \left( \frac{\delta W_z}{\delta z}\right)
  • Épaisseur de pression: \frac {\delta \left ( \frac {\delta p}{\delta sigma} \right )}{\delta t} = u \left[ \frac{\left (\frac {\delta p}{\delta sigma}\right )_x}{\delta x} \right] + v \left[ \frac{\left (\frac {\delta p}{\delta sigma}\right )_y}{\delta y} \right] + z \left[ \frac{\left (\frac {\delta p}{\delta sigma}\right )_z}{\delta z} \right]
Où \begin{cases}\Theta: Temp\acute{e}rature\ potentielle\ \\ \Phi: g\acute{e}opotentiel \\ \sigma: niveau\ sigma \end{cases}

Dans ce système de coordonnées, plusieurs variables (telles la température, la température potentielle et le contenu en eau) restent au même niveau sigma et se déplacent avec le vent à ce niveau. Ce dernier est calculé en utilisant la hauteur du géopotentiel, la chaleur spécifique, la fonction d’Exner (π) et le changement de niveau sigma.

Solution des équations primitives

La solution analytique des équations primitives donnent des ondes sinusoïdales qui varient dans le temps et l’espace. On peut donc la décomposer en harmoniques dont les coefficients sont reliés à la latitude et l’altitude, ce qui donne des ondes et marées atmosphériques.

\begin{Bmatrix}u, v, \phi \end{Bmatrix} = \begin{Bmatrix}\hat u, \hat v, \hat \phi \end{Bmatrix} e^{i(s \lambda + \sigma t)}
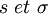s\ et\ \sigma sont respectivement le nombre d’onde zonal et la fréquence angulaire.

Pour obtenir cette solution, il faut linéariser les équations et en général les simplifier en utilisant des hypothèses souvent irréalistes (pas de dissipation des ondes, atmosphère isothermique, etc.). Dans les applications pratiques de ces équations, la prévision du temps par exemple, on utilise des méthodes d'analyse numérique qui font appel à la division des ondes en valeurs discrètes afin de tenir compte de toutes les variables.

Bibliographie

  • Beniston, Martin. From Turbulence to Climate: Numerical Investigations of the Atmosphere with a Hierarchy of Models. Berlin: Springer, 1998.
  • Firth, Robert. Mesoscale and Microscale Meteorological Model Grid Construction and Accuracy. LSMSA, 2006.
  • Pielke, Roger A. Mesoscale Meteorological Modeling. Orlando: Academic Press, Inc., 1984.
  • U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service. National Weather Service Handbook no 1 - Facsimile Products. Washington, DC: Department of Commerce, 1979.
  • Thompson, Philip. Numerical Weather Analysis and Prediction. New York: The Macmillan Company, 1961.

Notes

Voir aussi

Articles connexes

Liens externes

  • Katia Chancibault, « La prévision numérique météorologique », Risques hydro-météorologiques, crues et inondations, Laboratoire d'études des Transferts en Hydrologie et Environnement (LTHE). Consulté le 2006-12-28 [pdf]
  • Portail de la météorologie Portail de la météorologie
  • Portail de la physique Portail de la physique
Ce document provient de « %C3%89quations primitives atmosph%C3%A9riques ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equations primitives atmospheriques de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Équations primitives atmosphériques — Les équations primitives atmosphériques sont une version simplifiée des équations de Navier Stokes. Elles sont applicables dans le cas d’un fluide à la surface d’une sphère en posant comme hypothèses que la composante verticale du mouvement est… …   Wikipédia en Français

  • Équations de Navier-Stokes — Pour les articles homonymes, voir Stokes. En mécanique des fluides, les équations de Navier Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides « newtoniens » (visqueux) dans… …   Wikipédia en Français

  • Équations d'Euler —  Ne pas confondre avec l équation d Euler pour un polyèdre et diverses autres équations nommées d après Euler. L équation d Euler (établie par Leonhard Euler en 1755) s applique dans le cas d un fluide parfait, c’est à dire un fluide non… …   Wikipédia en Français

  • Météorologie — La météorologie a pour objet l étude des phénomènes atmosphériques tels que les nuages, les précipitations ou le vent dans le but de comprendre comment ils se forment et évoluent en fonction des paramètres mesurés tels que la pression, la… …   Wikipédia en Français

  • Meteo — Météorologie La météorologie est l étude des phénomènes atmosphériques tels que les nuages, les dépressions et les précipitations pour comprendre comment ils se forment et évoluent. Le mot vient du grec antique où meteor désigne les particules en …   Wikipédia en Français

  • Meteorologie — Météorologie La météorologie est l étude des phénomènes atmosphériques tels que les nuages, les dépressions et les précipitations pour comprendre comment ils se forment et évoluent. Le mot vient du grec antique où meteor désigne les particules en …   Wikipédia en Français

  • Météo — Météorologie La météorologie est l étude des phénomènes atmosphériques tels que les nuages, les dépressions et les précipitations pour comprendre comment ils se forment et évoluent. Le mot vient du grec antique où meteor désigne les particules en …   Wikipédia en Français

  • Météorologique — Météorologie La météorologie est l étude des phénomènes atmosphériques tels que les nuages, les dépressions et les précipitations pour comprendre comment ils se forment et évoluent. Le mot vient du grec antique où meteor désigne les particules en …   Wikipédia en Français

  • Météorologiques — Météorologie La météorologie est l étude des phénomènes atmosphériques tels que les nuages, les dépressions et les précipitations pour comprendre comment ils se forment et évoluent. Le mot vient du grec antique où meteor désigne les particules en …   Wikipédia en Français

  • Vent — Pour les articles homonymes, voir Vent (homonymie). Le vent est le mouvement d’une atmosphère, masse de gaz située à la surface d une planète. Les vents les plus violents connus ont lieu sur Neptune et sur Saturne. Il est essentiel à tous les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”