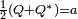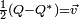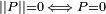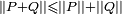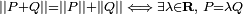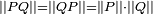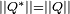- ℍ
-
Quaternion
 Plaque commémorative de la naissance des quaternions sur le pont de Broom (Dublin).
Plaque commémorative de la naissance des quaternions sur le pont de Broom (Dublin).
« Ici, le 16 octobre 1843, alors qu'il se promenait, Sir William Rowan Hamilton découvrit dans un éclair de génie la formule fondamentale sur la multiplication des quaternions
i² = j² = k² = ijk = -1
et la grava sur une pierre du pont. »
Un quaternion est un type de nombre hypercomplexe. L'ensemble des quaternions, noté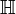 , constitue une extension de l'ensemble des nombres complexes, extension similaire à celle qui avait conduit de l'ensemble des nombres réels
, constitue une extension de l'ensemble des nombres complexes, extension similaire à celle qui avait conduit de l'ensemble des nombres réels  à celui des nombres complexes
à celui des nombres complexes  .
.Les quaternions furent mis en forme au XIXe siècle, par Hamilton qui cherchait à construire un ensemble de nombres ayant, dans l'espace, des propriétés analogues à celles que possèdent les nombres complexes dans le plan. Il les présente comme des quadruplets de réels.
L'ensemble des quaternions peut être muni d'une addition et d'une multiplication qui font de lui un des premiers exemples de corps non commutatif.
La relation qui existe entre les quaternions et les rotations en dimension 3 fait de l'ensemble des quaternions un outil utile pour le traitement de l'espace comme en infographie ou en théorie de la commande.
Origines et principes
Histoire
Les quaternions furent « découverts » par William Rowan Hamilton en 1843 à partir des travaux de Leonhard Euler et, au siècle suivant, Carl Friedrich Gauss. Il étudiait alors l'interprétation géométrique de l'arithmétique de nombres complexes dans le plan et cherchait à obtenir des résultats analogues dans l'espace à trois dimensions.
Après des années de recherches sur la construction d'une algèbre avec des « triplets » de trois nombres réels, il butait sur la multiplication, et en particulier la conservation des normes (Georg Ferdinand Frobenius a démontré en 1877 qu'une telle multiplication de triplets était impossible à définir).
Il eut alors l'idée d'utiliser des « quadruplets » en employant une dimension supplémentaire. Selon ses dires, il marchait, le 16 octobre 1843, le long du canal royal, avec son épouse quand soudain lui vint à l'esprit la solution sous la forme des relations : i2 = j2 = k2 = ijk = − 1. Il grava alors promptement ces relations avec un couteau dans une pierre du pont de Brougham (maintenant appelé Broom Bridge) à Dublin. Cette inscription, malheureusement effacée par le temps, a été remplacée par une plaque à la mémoire de Sir William Rowan Hamilton.
La théorie a été généralisée et d'autres ensembles comme les octonions ont été découverts par la suite. Un élément d'un ensemble de cette nature fut qualifiée de nombre hypercomplexe jusqu'à la Première Guerre mondiale. Ces ensembles sont maintenant considérés comme des exemples d'algèbres semi-simples. Le théorème d'Artin-Wedderburn fournit une méthode de construction générique et se fonde sur la théorie des représentations d'un groupe fini. La construction des quaternions est donnée dans l'article représentations du groupe des quaternions. Elle correspond à l'unique algèbre simple fidèle de la représentation du groupe de quaternions sur le corps des nombres réels.
Principe
Hamilton décrivit un quaternion comme un quadruplet de nombres réels, le premier élément étant un « scalaire », et les trois éléments restants formant un « vecteur », ou « imaginaire pur ».
Il put ainsi définir une multiplication avec les bonnes propriétés. Celle-ci peut se résumer à cette table de multiplication :
· 1 i j k 1 1 i j k i i -1 k -j j j -k -1 i k k j -i -1 Tout quaternion H peut être considéré comme une combinaison linéaire des quatre quaternions "unités" 1, i, j, et k :
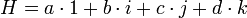
(où a, b, c, d sont des nombres réels).H peut également s'écrire: H = z + z'·j (avec z et z' des nombres complexes de la forme a + b·i)
Les nombres réels a, b, c et d sont caractéristiques de H : il n'existe qu'une seule façon d'écrire H sous cette forme, et tout quaternion comportant ces mêmes 4 caractéristiques est nécessairement égal à H (la réciproque est vraie).
a s'appelle la composante réelle ou scalaire de H, tandis que b, c et d sont les composantes complexes de H. On dit aussi que a est le scalaire de H et que le triplet {b, c, d} ou [
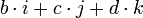 ] est le vecteur de H (ou sa partie vectorielle).
] est le vecteur de H (ou sa partie vectorielle).Cette découverte entraîna l'abandon de l'utilisation exclusive des lois commutatives, une avancée radicale pour l'époque. Les vecteurs et les matrices faisaient encore partie du futur, mais Hamilton venait en quelque sorte d'introduire le produit vectoriel et le produit scalaire des vecteurs.
Non-commutativité
L'algèbre des quaternions n'est plus commutative, mais partiellement anticommutative : 1 · i = i · 1 = i mais i · j = k et j · i = -k.
Cette non commutativité est d'ailleurs tout à fait compatible avec une interprétation géométrique des quaternions, par exemple les rotations vectorielles du plan sont commutatives, mais celles de l'espace ne le sont pas :
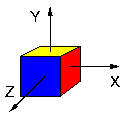
- On effectue une rotation autour de l'axe X suivie d'une rotation autour de l'axe Y:
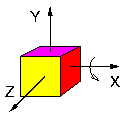
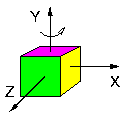
- On effectue une rotation autour de l'axe Y suivie d'une rotation autour de l'axe X:
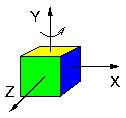
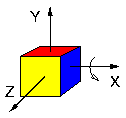
- Les deux cubes ont subi les mêmes rotations, mais dans un ordre différent. Le résultat final est différent, ce qui exprime de façon graphique la non-commutativité des rotations.
Propriétés mathématiques
Classification algèbrique
Le théorème de Frobenius généralisé (1877) montre que les extensions du corps des réels
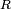 sont peu nombreuses. De fait, il n'en existe que quatre : le corps des réels
sont peu nombreuses. De fait, il n'en existe que quatre : le corps des réels 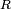 , lui-même, celui des nombres des complexes
, lui-même, celui des nombres des complexes 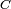 , celui des quaternions
, celui des quaternions 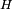 et celui des octonions
et celui des octonions 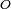 . Le corps des quaternions n'est pas commutatif et celui de octonions n'est pas associatif. Dans ce contexte, les quaternions peuvent être définis comme le plus petit corps non-commutatif contenant
. Le corps des quaternions n'est pas commutatif et celui de octonions n'est pas associatif. Dans ce contexte, les quaternions peuvent être définis comme le plus petit corps non-commutatif contenant 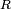 .
.Dans le même ordre d'idée, le théorème de Hurwitz (1898) montre que les algèbres de composition sur un corps K, c'est-à-dire les algèbres munies d'une norme non-dégénérée, sont de dimensions 1, 2, 4 ou 8. Ces algèbres peuvent être obtenues à partir de la construction de Cayley-Dickson. De plus
- les algèbres de composition de dimension 1 n'existent que lorsque char(K) ≠ 2.
- les algèbres de composition de dimension 1 et 2 sont commutatives et associatives.
- les algèbres de composition de dimension 2 sont ou bien des extensions quadratiques de K, ou bien isomorphes à
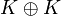 .
. - les algèbres de composition de dimension 4 sont des algèbres de quaternions. Elles sont associatives mais pas commutatives.
- les algèbres de composition de dimension 8 sont des algèbres d'octonions. Elles ne sont ni associatives, ni commutatives.
Définition
L'espace vectoriel des quaternions H sur le corps des réels est un espace vectoriel réel de dimension quatre rapporté à une base notée
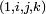 . Tout quaternion
. Tout quaternion 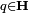 , s'écrit donc de manière unique
, s'écrit donc de manière unique 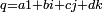 .
.Scalaires et vecteurs
L'ensemble des quaternions de la forme
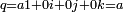 s'identifie aux nombres réels. Ils sont appelés scalaires ou réels.
s'identifie aux nombres réels. Ils sont appelés scalaires ou réels.Les quaternions de la forme
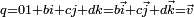 , forment un espace vectoriel tridimensionel, identifié à
, forment un espace vectoriel tridimensionel, identifié à 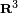 , par identification des bases
, par identification des bases 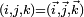 . On les appelle quaternions purs, quaternions vectoriels, ou par abus de langage, vecteurs.
. On les appelle quaternions purs, quaternions vectoriels, ou par abus de langage, vecteurs.Tout quaternion q se décompose en une somme d'un réel et d'un vecteur
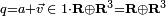 , appelées partie scalaire (ou réelle) et partie vectorielle de q. Cette décomposition est unique.
, appelées partie scalaire (ou réelle) et partie vectorielle de q. Cette décomposition est unique.Addition
La somme de deux quaternions
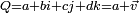 et
et 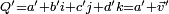 , est définie composant par composant par:
, est définie composant par composant par: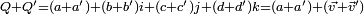
Cette addition fait de H un groupe abélien(commutatif) par transport de structure.
Son élement neutre est
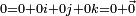 et l'opposé d'un quaternion
et l'opposé d'un quaternion 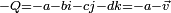 s'obtient en inversant les signes de ses composants.
s'obtient en inversant les signes de ses composants.Multiplication de Hamilton
Le produit de deux quaternions
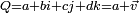 et
et 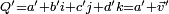 , s'obtient en développant le produit formellement, puis en effectuant les réductions
, s'obtient en développant le produit formellement, puis en effectuant les réductions 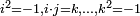 définies par la table de multiplication donnée plus haut.
définies par la table de multiplication donnée plus haut.Tous calculs faits, on obtient
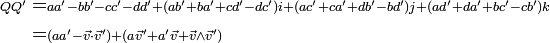 .
.Dans cette dernière formule le
 désigne le produit scalaire et
désigne le produit scalaire et  le produit vectoriel des composantes vectorielles des deux quaternions.
le produit vectoriel des composantes vectorielles des deux quaternions.Cette multiplication fait de H un anneau associatif unitaire, la distributivité résultant de la bilinéarité des produits scalaires et vectoriels.
Pour tout quaternion
 , on a :
, on a :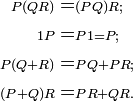
Non-commutativité
La multiplication n'est pas commutative. De fait, la formule précédente montre que pour que
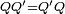 , il faut et il suffit que
, il faut et il suffit que 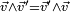 , c'est-à-dire que leurs composantes vectorielles soient colinéaires.
, c'est-à-dire que leurs composantes vectorielles soient colinéaires.En particulier, un quaternion commute à tous les quaternions si, et seulement si, sa partie vectorielle est nulle, c'est-à-dire s'il est réel. Pour
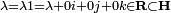 , la formule
, la formule 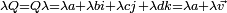 , définit alors une multiplication externe qui munit H d'une structure d'espace vectoriel. Cette opération préserve le sous-espace des scalaires R et des vecteurs R3. Sur ces sous-espaces, elle coïncide avec les multiplications habituelles.
, définit alors une multiplication externe qui munit H d'une structure d'espace vectoriel. Cette opération préserve le sous-espace des scalaires R et des vecteurs R3. Sur ces sous-espaces, elle coïncide avec les multiplications habituelles.En résumé:
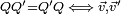 colinéaires
colinéaires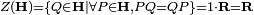
Conjugaison, norme, inversion
Les quaternions sont munis d'une conjugaison, qui est un anti-morphisme involutif, qui permet de définir une norme, puis l'inverse d'un quaternion. On vérifie alors que H est un corps.
Conjugaison
Le conjugué du quaternion
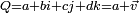 est le quaternion obtenu en conservant sa partie scalaire et en prenant l'opposé de sa partie vectorielle
est le quaternion obtenu en conservant sa partie scalaire et en prenant l'opposé de sa partie vectorielle 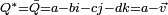 .
.On remarquera que le conjugué d'un scalaire
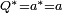 est lui-même et que le conjugué d'un vecteur pur
est lui-même et que le conjugué d'un vecteur pur 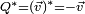 est son opposé. Pour cette raison Hamilton se référait à la conjugaison comme inverse spatial.
est son opposé. Pour cette raison Hamilton se référait à la conjugaison comme inverse spatial.La conjugaison est linéaire, i.e.
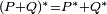 , et un anti-morphisme, inversant le sens du produit
, et un anti-morphisme, inversant le sens du produit 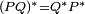
C'est une involution, égale à son propre inverse
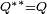 .
.Les invariants, tels que
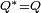 , sont les réels et les anti-invariants, tels que
, sont les réels et les anti-invariants, tels que 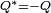 , sont les quaternions purs.
, sont les quaternions purs.La conjugaison permet de retrouver facilement la partie réelle et vectorielle d'un quaternion
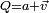 :
:Norme
Le produit d'un quaternion
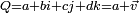 par son conjugué Q * donne
par son conjugué Q * donne 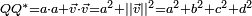 qui est un nombre réel positif.
qui est un nombre réel positif.On appelle norme du quaternion
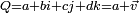 , le nombre réel positif
, le nombre réel positif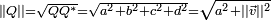 .
.
Cette norme dérive du produit scalaire canonique sur R4, défini par
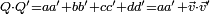 . Elle coïncide avec la norme euclidienne dans l'espace quadri-dimensionel R4, sa restriction aux scalaires avec la valeur-absolue et sa restriction aux vecteurs avec la norme usuelle dans l'espace tridimensionel standard.
. Elle coïncide avec la norme euclidienne dans l'espace quadri-dimensionel R4, sa restriction aux scalaires avec la valeur-absolue et sa restriction aux vecteurs avec la norme usuelle dans l'espace tridimensionel standard.On a :
Inverses et divisions
Si un quaternion
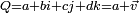 n'est pas nul, il possède un unique inverse
n'est pas nul, il possède un unique inverse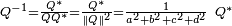
.
Si
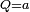 est réel, son inverse
est réel, son inverse 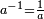 est l'inverse de a en tant que réel. Et si
est l'inverse de a en tant que réel. Et si 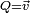 est un vecteur, son inverse
est un vecteur, son inverse 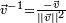 est le vecteur pointant dans la direction opposée à
est le vecteur pointant dans la direction opposée à 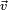 et de norme inverse.
et de norme inverse.La multiplication n'étant pas commutative, on peut définir la division du quaternion
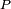 par le quaternion (non nul)
par le quaternion (non nul) 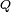 de deux façons différentes :
de deux façons différentes :- la division à gauche
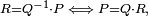
- la division à droite
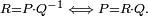
Conjugué d'un inverse, conjugué de la somme et du produit de deux quaternions
On montre aisément les égalités :
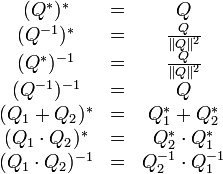
Quaternions unitaires et forme polaire
Quaternions unitaires
Les quaternions unitaires sont, par définition, les quaternions de norme 1. Leur ensemble est topologiquement isomorphe à la sphère S3.
Un quaternion est unitaire si, et seulement si,
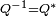 , de sorte que la restriction du produit de Hamilton aux quaternions unitaires fait de la sphère unitaire un groupe multiplicatif. Nous verrons plus loin que ce groupe agit par rotation sur l'espace tridimensionnel des quaternions purs.
, de sorte que la restriction du produit de Hamilton aux quaternions unitaires fait de la sphère unitaire un groupe multiplicatif. Nous verrons plus loin que ce groupe agit par rotation sur l'espace tridimensionnel des quaternions purs.Ils forment une sphère, et nous verrons ci-dessous qu'on peut établir une sorte de correspondance entre un quaternion unitaire et une rotation vectorielle dans l'espace euclidien de dimension 3, et que cette particularité permet une représentation simple du produit de deux rotations vectorielles.
Versors
Pour tout quaternion Q, le quaternion
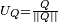 est un quaternion unitaire, appelé versor (ou verseur) de Q.
est un quaternion unitaire, appelé versor (ou verseur) de Q.Tout quaternion apparait donc comme le produit
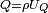 d'un nombre réel positif
d'un nombre réel positif 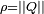 par un quaternion unitaire.
par un quaternion unitaire.On remarquera que
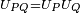 et que
et que 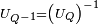 .
.Par ailleurs,
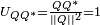 , d'où on déduit que
, d'où on déduit que 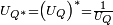 .
.Forme polaire
On peut poursuivre plus loin la décomposition précédente. En effet, de
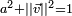 , pour un quaternion unitaire
, pour un quaternion unitaire 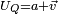 , on tire l'existence d'un réel
, on tire l'existence d'un réel  , tel que
, tel que 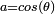 et
et 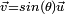 où
où 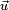 est un vecteur unitaire de R3.
est un vecteur unitaire de R3.Finalement, tout quaternion s'écrit sous la forme
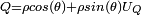 , où
, où 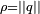 est un réel positif et uQ est un quaternion unitaire de composante réelle nulle, représenté par
est un réel positif et uQ est un quaternion unitaire de composante réelle nulle, représenté par 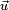 , vecteur de la sphère
, vecteur de la sphère 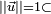 R3. Si Q est non réel, cette décomposition est unique, à
R3. Si Q est non réel, cette décomposition est unique, à 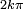 près pour θ ; si Q est réel, le choix de
près pour θ ; si Q est réel, le choix de 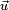 est arbitraire.
est arbitraire.Il est possible de définir (par la série usuelle) une fonction exponentielle dans les quaternions, et l'on montre qu'avec les notations précédentes, on a
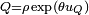 .
.Sous-ensembles particuliers
Racines carrées
Le corps des quaternions n'étant pas commutatif, un polynôme peut avoir plus de racines distinctes que son degré.
Considérons par exemple, le polynôme
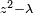 , où
, où 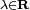 dont les racines sont les racines carrées du nombre réel λ. En écrivant
dont les racines sont les racines carrées du nombre réel λ. En écrivant 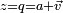 , elle devient
, elle devient 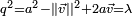 . La partie vectorielle de ce carré étant nulle, on doit avoir
. La partie vectorielle de ce carré étant nulle, on doit avoir 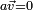 , c'est-à-dire, soit
, c'est-à-dire, soit 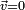 , auquel cas
, auquel cas 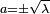 , soit
, soit 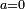 , auquel cas
, auquel cas 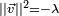 , ce qui montre que les racines carrées d'un nombre réel négatif sont situées sur une sphère dans l'espace R3.
, ce qui montre que les racines carrées d'un nombre réel négatif sont situées sur une sphère dans l'espace R3.Pour trouver les racines d'un quaternion général
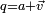 , écrivons sa racine sous sa forme polaire
, écrivons sa racine sous sa forme polaire 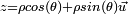 , avec, avec
, avec, avec 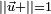 . Un calcul immédiat donne
. Un calcul immédiat donne 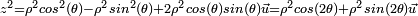 . D'où on déduit successivement
. D'où on déduit successivement 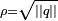 , au signe près; puis
, au signe près; puis  de
de 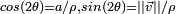 , à
, à  près; puis
près; puis 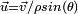 .
.On est donc dans l'un des cas suivants:
- La racine carrée de
 est 0 ;
est 0 ; - Les racines carrées d'un réel
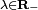 négatif sont les vecteurs de la sphère d'équation
négatif sont les vecteurs de la sphère d'équation 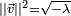 ;
; - Un quaternion qui n'est pas un réel négatif, possède deux racines carrées opposées.
Sous-algèbres
Pour un quaternion non réel
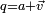 avec
avec 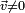 , on peut écrire
, on peut écrire 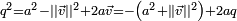 . Donc
. Donc 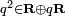 et, par récurrence,
et, par récurrence, 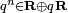 . Ceci montre que la sous-algèbre engendrée par un quaternion q non réel est
. Ceci montre que la sous-algèbre engendrée par un quaternion q non réel est 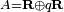 . C'est aussi la sous-algèbre engendrée
. C'est aussi la sous-algèbre engendrée 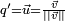 . Or ce dernier élément est tel que
. Or ce dernier élément est tel que 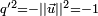 . La sous-algèbre est donc isomorphe au plan complexes C.
. La sous-algèbre est donc isomorphe au plan complexes C.Si une sous-algèbre A contient deux quaternions
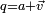 et
et 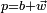 , alors elle contient aussi le quaternion
, alors elle contient aussi le quaternion 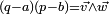 . Donc, si
. Donc, si 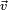 et
et 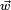 ne sont pas colinéaires, A contient tout l'espace R3, et, par suite, A = H.
ne sont pas colinéaires, A contient tout l'espace R3, et, par suite, A = H.En résumé, les sous-algèbres de H sont
- Les sous-algèbres triviales R et H ;
- Une infinité de plans isomorphes au corps des complexe C, l'image de i pouvant être pris comme n'importe quel élément arbitraire de la sphère S2 des quaternions unitaires purs.
La notation (a, V)
Le quaternion
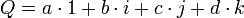 peut être décomposé (et de façon unique) en un couple formé du réel
peut être décomposé (et de façon unique) en un couple formé du réel  et du vecteur
et du vecteur 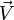 de
de 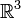 dont les coordonnées sont (b,c,d).
dont les coordonnées sont (b,c,d).On écrit :
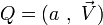 .
.Cette notation permet de définir la somme et le produit de la façon suivante :
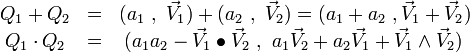
Elle permet aussi de re-définir ou définir les 3 notions suivantes :- le conjugué
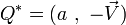 de
de 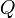 ,
, - le produit scalaire de deux quaternions :
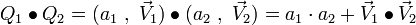
d'où l'on déduit :
- la norme d'un quaternion :
nota : le produit scalaire défini ci-dessus est commutatif et il est donc bien sûr différent du produit de quaternions défini plus haut.
Soit à présent un quaternion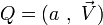 quelconque ; notons
quelconque ; notons 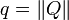 et
et 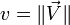 . Si le réel
. Si le réel 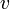 positif n'est pas nul, le réel
positif n'est pas nul, le réel 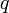 ne l'est pas non plus et l'on peut donc toujours écrire :
ne l'est pas non plus et l'on peut donc toujours écrire :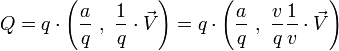
Or
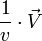 est un vecteur normé et l'on peut écrire :
est un vecteur normé et l'on peut écrire : 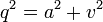 , ou encore :
, ou encore : 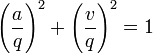 .
.Il en résulte qu'il existe :
- un angle
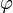 (dont le cosinus et le sinus valent respectivement
(dont le cosinus et le sinus valent respectivement  et
et  ) et
) et - un vecteur normé
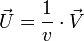
qui sont tels que l'on puisse écrire le quaternion
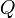 (de vecteur
(de vecteur 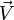 non nul) sous la forme :
non nul) sous la forme :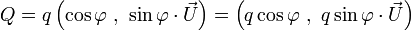
Cette façon d'écrire un quaternion est importante : les termes du couple,
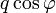 et
et 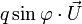 , sont en effet respectivement le produit scalaire et le produit vectoriel de deux vecteurs
, sont en effet respectivement le produit scalaire et le produit vectoriel de deux vecteurs 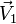 et
et 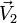 orthogonaux à
orthogonaux à 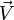 , ces 2 vecteurs faisant entre eux un angle égal à
, ces 2 vecteurs faisant entre eux un angle égal à 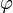 . Et cette écriture permet de construire la multiplication des quaternions grâce à la composition des similitudes de
. Et cette écriture permet de construire la multiplication des quaternions grâce à la composition des similitudes de  ³ comme on peut le voir en cliquant ici
³ comme on peut le voir en cliquant iciLes similitudes de l'espace et les quaternions
Pour démystifier les quaternions, nous allons faire un petit détour instructif par la géométrie élémentaire et en particulier par les similitudes dans l'espace. Une similitude dans
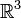 est entièrement définie par la triple donnée :
est entièrement définie par la triple donnée :- d'un axe de rotation bien orienté (un vecteur unitaire U),
- d'un angle 2φ défini à 2kπ près et
- d'un rapport d'homothétie k, un réel strictement positif.
L'effet d'une similitude sur tous les vecteurs peut être considéré grossièrement comme un vissage avec expansion.
Voyage et trajets
Plus précisément, l'image du transformé d'un vecteur V (dont l'origine est supposée située sur l'axe U) est obtenue d'abord par une multiplication (homothétie) de ce vecteur par k, suivi par une rotation d'angle 2φ autour de l'axe de rotation (on pourrait aussi commencer par la rotation et la faire suivre de l'homothétie, mais il faudrait modifier un peu les explications qui vont suivre...). Cette rotation fait tourner d'un angle 2φ l'extrémité du vecteur kV sur un cercle (C) centré sur l'axe et situé dans un plan perpendiculaire à U. Or sur ce cercle, il y a deux façons d'effectuer le trajet : soit en utilisant un arc, soit en utilisant son complémentaire, ces arcs ne pouvant pas malheureusement être distingués par la seule mesure 2φ + 2kπ.
C'est précisément cette difficulté que permet de résoudre la notion de quaternion. Schématiquement, on peut dire qu'un quaternion, c'est comme une similitude qui saurait distinguer les 2 trajets que peut emprunter la rotation associée.Dans la vie courante, si pour un voyage entre deux localités L1 et L2, vous avez a priori deux trajets possibles, la distinction entre ces trajets peut être faite en désignant deux sites-étapes intermédiaires s1 et s2. Et en parlant du trajet s1 et du trajet s2, vous sous-entendrez les localités de départ et d'arrivée L1 et L2.
En conservant cette analogie, il nous faut donc définir deux points intermédiaires sur les deux arcs du trajet.
À mi-chemin
Les points situés à mi-chemin sont parfaits pour cette mission. En effet, si je divise l'angle de vecteurs 2φ + 2kπ par 2, j'obtiens deux angles distincts φ + 2kπ et φ-π + 2kπ. Or, si j'utilise la rotation d'axe U et d'angle φ + 2kπ, je définis un site-étape différent de celui que j'obtiens avec la rotation φ-π + 2kπ. Ainsi à la similitude sim(U, 2φ, k), il correspond deux trajets distincts qui sont représentés par les deux quaternions distincts quat(U, φ, k) et quat(U, −π+φ, k).
Le formalisme
Le triplet (U, φ, k) peut s'écrire de façon équivalente sous la forme du couple (kcos(φ), ksin(φ)∙U) de la notation (a, V). Et en utilisant des vecteurs a et b orthogonaux à U convenables, il est facile de montrer que ce couple prend la forme (a.b, a^b). Ainsi, nos sites-étapes nous permettent de revenir à des opérations très simples sur des vecteurs. Et comme ces opérations sont riches de propriétés remarquables, on sait définir (comme on l'a vu ci-dessus) une multiplication et une addition des quaternions. Vous pouvez « voir » ces deux opérations sur les quaternions ici : http://www.alcys.com
Une voie de recherche prometteuse peut être consultée sur le site [1]. On y définit justement la similitude dans l'espace à trois dimensions par un bivecteur qui est au couple de vecteurs ce que le vecteur est au couple de points. La loi de composition introduite dans ces bivecteurs est effectivement non commutative, et la restriction de cet ensemble au plan est l'ensemble des complexes.
Double produit de quaternions
De même que l'on peut calculer un double produit vectoriel, il est possible de calculer un double produit de quaternions.
Correspondance entre quaternion unitaire et rotation vectorielle
On peut démontrer que le transformé
![\vec V' = \mathbf R_{\left[2\varphi, \vec N\right]}(\vec V) \,](/pictures/frwiki/53/5d416c2b9af7eb7a1b168bfcc1b35300.png) de tout vecteur
de tout vecteur 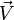 quelconque (de l'espace euclidien de dimension 3) dans la rotation
quelconque (de l'espace euclidien de dimension 3) dans la rotation ![\mathbf R\left[2\,\varphi,\,\vec N\right]](/pictures/frwiki/49/1a4d2920c321cd4787f62ecae7bdb501.png) d'angle
d'angle 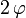 et d'axe
et d'axe 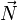 (
(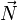 étant un vecteur normé) peut être calculé grâce au produit de quaternions suivants :
étant un vecteur normé) peut être calculé grâce au produit de quaternions suivants :
![(0,\ \vec V') = \left(0,\ \mathbf R_{\left[2\varphi, \vec N\right]}(\vec V)\right) = (\cos \varphi,\ \sin \varphi\ \vec N)\cdot
(0,\ \vec V)\cdot (\cos \varphi,\ -\sin \varphi\ \vec N)](/pictures/frwiki/99/c45d7dbec8f7e7b7940a0654a7b2cfae.png)
où
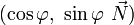 et
et 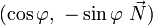 sont deux quaternions unitaires conjugués et où
sont deux quaternions unitaires conjugués et où 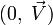 et
et 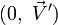 sont des quaternions dont la composante scalaire est nulle.
sont des quaternions dont la composante scalaire est nulle.On peut aussi écrire cette transformation avec la notation
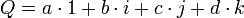 . Si la rotation est autour d'un axe orienté selon le vecteur
. Si la rotation est autour d'un axe orienté selon le vecteur 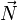 de coordonnées (x, y,z) (le vecteur étant normé) et d'angle
de coordonnées (x, y,z) (le vecteur étant normé) et d'angle 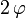 , le quaternion associé vaut :
, le quaternion associé vaut :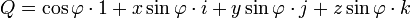
Composition de rotations vectorielles et produit de quaternions
La propriété précédente justifie le fait que l'on a coutume de dire, mais de façon peu rigoureuse, que le quaternion
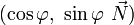 représente la rotation
représente la rotation ![\mathbf R\left[2\,\varphi,\,\vec N\right]](/pictures/frwiki/49/1a4d2920c321cd4787f62ecae7bdb501.png) .
.En utilisant le même langage approximatif, on peut dire que la composition de deux rotations successives
 puis
puis  est une rotation
est une rotation 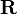 qui est représentée par le quaternion
qui est représentée par le quaternion 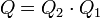 , les quaternions
, les quaternions 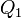 et
et 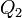 étant les représentants respectifs des rotations
étant les représentants respectifs des rotations 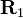 et
et 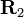 .
.Montrons-le :
En posant :
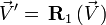 , puis
, puis 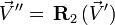 , la formule encadrée ci-dessus nous donne, écrite de façon condensée, les 2 égalités :
, la formule encadrée ci-dessus nous donne, écrite de façon condensée, les 2 égalités :
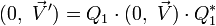 et
et
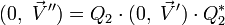 , ce qui peut donc encore s'écrire :
, ce qui peut donc encore s'écrire :
![(0,\ \vec V'') = Q_2\cdot \left[Q_1\cdot (0,\ \vec V)\cdot Q^*_1\right]\cdot Q^*_2](/pictures/frwiki/98/b999ec46005e5d488ffeebdd64c524a5.png) ou, si l'on tient compte de l'associativité du produit de quaternions:
ou, si l'on tient compte de l'associativité du produit de quaternions:
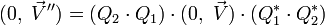 , ou encore :
, ou encore :
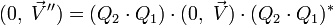 , en tenant compte de la valeur du conjugué de deux quaternions.
, en tenant compte de la valeur du conjugué de deux quaternions.Ce qui établit la propriété annoncée pour la composition de deux rotations et que nous écrirons :
![\Bigg(0,\ \mathbf R_{\left[2\varphi_2, \vec N_2\right]}\left(\mathrm R_{\left[2\varphi_1, \vec N_1\right]} (\vec V)\right)\Bigg) =
(\cos \varphi_2,\ \sin \varphi_2\ \vec N_2)
\cdot
(\cos \varphi_1,\ \sin \varphi_1\ \vec N_1)
\cdot
(0,\ \vec V)
\cdot
(\cos \varphi_1,\ -\sin \varphi_1\ \vec N_1)
\cdot
(\cos \varphi_2,\ -\sin \varphi_2\ \vec N_2)](/pictures/frwiki/49/1087ff1423ed4d32a168f8287e4ea877.png)
Notations matricielles
De même qu'il est possible de mettre en correspondance le nombre complexe
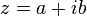 avec la matrice :
avec la matrice : 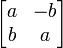 , il est possible de faire correspondre le quaternion
, il est possible de faire correspondre le quaternion 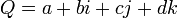 avec la matrice complexe suivante :
avec la matrice complexe suivante :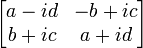
ou encore avec la matrice réelle suivante :
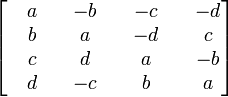
Il existe plusieurs représentations matricielles d'un quaternion. La matrice précédente en est une[1]. Celle qui suit est plus souvent utilisée. Ainsi, la matrice réelle créée à partir d'un quaternion s'écrit de cette façon (en gardant q=a+ib+jc+kd):
Si le quaternion unitaire représente une rotation depuis l'origine, on peut le représenter à l'aide d'une matrice 3x3
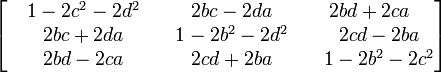
Avec ces équivalences, la somme et le produit de deux quaternions correspondent respectivement à la somme et au produit des matrices qui leur correspondent.
Remarque :
La matrice complexe
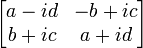 peut encore s'écrire sous la forme :
peut encore s'écrire sous la forme :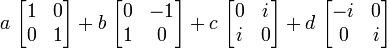
où les 4 matrices :
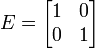 ,
, 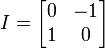 ,
, 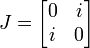 et
et 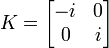 sont les matrices complexes qui correspondent aux quatre quaternions-unités 1, i, j et k évoquées dans la première définition des quaternions.
sont les matrices complexes qui correspondent aux quatre quaternions-unités 1, i, j et k évoquées dans la première définition des quaternions.Applications
Alors que cela est discutable en dimension 3, les quaternions ne peuvent pas être employés dans d'autres dimensions (bien que des extensions comme celles des biquaternions et des algèbres de Clifford soient utilisables). De toute façon, la notion de vecteur avait presque universellement remplacé celle des quaternions en science et en technologie dans le milieu du XXe siècle.
Aujourd'hui, les quaternions trouvent leur place en infographie, en théorie de la commande, dans le traitement du signal, dans la commande de mouvement et la mécanique orbitale, principalement pour représenter les rotations et les orientations en dimension 3. Par exemple, il est fréquent que les systèmes de commande de déplacement d'un vaisseau spatial soient régis en termes de quaternions. La raison est qu'effectuer beaucoup d'opérations sur les quaternions est numériquement plus stable que d'effectuer beaucoup d'opérations sur les matrices.
Interpolation de rotations
Si l'on prend deux rotations de l'espace ra et rb, l'interpolation linéaire de ces rotations n'est en général pas une rotation. Pour pouvoir interpoler, il faut soit
- utiliser les angles d'Euler,
- utiliser les quaternions.
Dans le dernier cas, les 2 rotations sont représentées par 2 quaternions qa et qb sur la sphère unité S3, et l'interpolation correspond à la géodésique entre ces 2 points
Sources
- ↑ P. Girard, Quaternions, algèbre de Clifford et physique relativiste, PPUR, 2004, ISBN 2-88074-606-X
Voir aussi
Articles connexes
- Quaternions et rotation dans l'espace
- groupe de quaternions
- biquaternion
- matrice de Dirac
- algèbre d'espace-temps
- Adolf Hurwitz
Liens externes
- Portail des mathématiques
Catégories : Nombre hypercomplexe | Théorie des corps | Géométrie
Wikimedia Foundation. 2010.