ℋ

ℋ: Mécanique hamiltonienne

Pour les articles homonymes, voir Hamilton.

La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l'élaboration théorique de la mécanique quantique.

Sommaire

1 Équations canoniques de Hamilton

1.1 Rappels de mécanique lagrangienne

1.2 Moment conjugué

1.3 Hamiltonien

1.4 Équations canoniques de Hamilton

1.5 Exemple élémentaire : la particule non relativiste sur un axe

2 Espace des phases

2.1 Dynamique dans l'espace euclidien

2.2 Dynamique sur une variété différentiable

3 Flot hamiltonien

3.1 Théorème de Liouville

3.2 Hypersurface d'énergie constante

3.3 Système intégrable

4 Articles connexes

5 Bibliographie

Équations canoniques de Hamilton

Rappels de mécanique lagrangienne

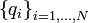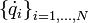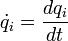En mécanique lagrangienne, les équations du mouvement d'un système à N degrés de liberté dépendent des coordonnées généralisées $\left\{q_i \right\}_{i=1,...,N}$ et des vitesses correspondantes $\left\{ \dot{q}_i \right\}_{i=1,...,N}$ , où $\dot{q}_i = \dfrac{dq_i}{dt}$ .

Le lagrangien peut donc s'écrire formellement comme une fonction : 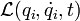$\mathcal{L} (q_i, \dot{q}_i, t)$ , les variables indexées représentant les $N$ variables de ce type.

Moment conjugué

En mécanique hamiltonienne, chaque vitesse généralisée est remplacée par la quantité de mouvement associée, aussi appelée moment conjugué ou encore impulsion généralisée :

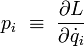
$p_i \ \equiv \ {\partial L \over \partial \dot{q}_i}$

En coordonnées cartésiennes, les quantités de mouvement sont équivalentes aux moments linéaires, alors qu'en coordonnées polaires elles correspondent aux moments angulaires. Lorsque les coordonnées généralisées sont choisies arbitrairement, il n'est plus possible de donner une interprétation intuitive aux moments conjugués.

Hamiltonien

L'hamiltonien $\mathcal{H}$ est la transformée de Legendre du lagrangien :

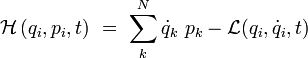
$\mathcal{H} \left(q_i,p_i,t\right) \ = \ \sum_k^N \dot{q}_k \ p_k - \mathcal{L}(q_i,\dot{q}_i,t)$

Dans le membre de droite de cette formule, les vitesses sont supposées être exprimées en fonction des moments conjugués.

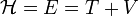Si les équations qui définissent les coordonnées généralisées sont indépendantes du temps t, on peut montrer que $\mathcal{H}$ est égal à l'énergie totale E, elle-même étant égale à la somme de l'énergie cinétique T et de l'énergie potentielle V ( $\mathcal{H} = E = T + V$ ).

Équations canoniques de Hamilton

Sous forme différentielle, les deux membres de la définition de $\mathcal{H}$ deviennent :

$\begin{matrix} d \mathcal{H} &=& \sum_i \left[ \left({\partial \mathcal{H} \over \partial q_i}\right) dq_i + \left({\partial \mathcal{H} \over \partial p_i}\right) dp_i\right] + \left({\partial \mathcal{H} \over \partial t}\right) dt \\ d \mathcal{H} &=& \sum_i \left[ \dot{q}_i dp_i + p_i d\dot{q}_i - \left({\partial \mathcal{L} \over \partial q_i}\right) dq_i - \left({\partial \mathcal{L} \over \partial \dot{q}_i}\right) d\dot{q}_i \right] - \left({\partial \mathcal{L} \over \partial t}\right) dt \end{matrix}$

En utilisant la définition des moments conjugués donnée précédemment et les équations d'Euler Lagrange traduisant le principe de l'action minimale du lagrangien, on obtient les équations du mouvement de Hamilton, dites équations canoniques de Hamilton :

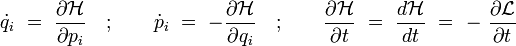
$\dot{q}_i \ = \ \frac{\partial \mathcal{H}}{\partial p_i} \quad ; \qquad \dot{p}_i \ = \ - \frac{\partial \mathcal{H}}{\partial q_i} \quad ; \qquad \frac{\partial \mathcal{H}}{\partial t } \ = \ \frac{d\mathcal{H}}{dt} \ = \ - \ \frac{\partial \mathcal{L} }{\partial t}$

Note: l'égalité 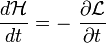$\frac{d\mathcal{H}}{dt}=- \ \frac{\partial \mathcal{L} }{\partial t}$ se démontre comme suit: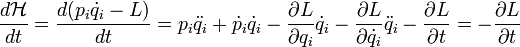

$\frac{d\mathcal{H}}{dt}=\frac{d(p_i \dot{q}_i-L)}{dt}=p_i \ddot{q}_i+\dot{p}_i\dot{q}_i-\frac{\partial L}{\partial q_i} \dot{q}_i-\frac{\partial L}{\partial \dot{q}_i}\ddot{q}_i-\frac{\partial L}{\partial t}=-\frac{\partial L}{\partial t}$

Où on a utilisé pour la dernière égailté la définition des moments conjugués.

Les équations de Hamilton sont des équations différentielles du premier ordre et donc plus faciles à résoudre que les équations de Lagrange qui sont du second ordre. Néanmoins, les étapes qui conduisent à ces équations sont plus complexes que celles de la mécanique lagrangienne : à partir des coordonnées généralisées et du lagrangien, il faut calculer l'hamiltonien, exprimer les vitesses généralisées en fonction des moments conjugués et remplacer celles-ci dans la définition de l'hamiltonien.

La méthode de Lagrange est moins lourde en termes de manipulations mathématiques. L'avantage principal de l'approche hamiltonienne est de fournir, grâce à la simplicité de son formalisme, un fondement théorique en mécanique. Par exemple, la mécanique quantique utilise un formalisme basé sur celui de la mécanique hamiltonienne.

On pourra aussi noter une certaine similitude entre les équations canoniques de Hamilton et les équations de Maxwell.

Exemple élémentaire : la particule non relativiste sur un axe

Soit une particule non relativiste de masse m se déplaçant sur un axe. On repère la position de cette particule par une coordonnée q. Supposons de plus que la particule est soumise à une force qui dérive de l'énergie potentielle V(q). Le lagrangien s'écrit alors :

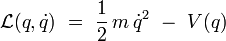
$\mathcal{L}(q, \dot{q}) \ = \ \frac{1}{2} \, m \, \dot{q}^2 \ - \ V(q)$

Le moment conjugué vaut alors :

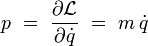
$p \ = \ {\partial \mathcal{L} \over \partial \dot{q}} \ = \ m \, \dot{q}$

il s'identifie à la quantité de mouvement habituelle. Cette formule peut être inversée :

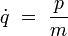
$\dot{q} \ = \ \frac{p}{m}$

On obtient alors le hamiltonien par transformée de Legendre :

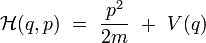
$\mathcal{H}(q, p) \ = \ \frac{p^2}{2m} \ + \ V(q)$

Les équations canoniques conduisent alors à :

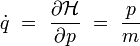
$\dot{q} \ = \ \frac{\partial \mathcal{H}}{\partial p} \ = \ \frac{p}{m}$

et à l'équation de la dynamique de Newton :

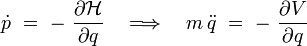
$\dot{p} \ = \ - \ \frac{\partial \mathcal{H}}{\partial q} \quad \Longrightarrow \quad m \, \ddot{q} \ = \ - \ \frac{\partial V}{\partial q}$

Espace des phases

Dynamique dans l'espace euclidien

Considérons un système à $N$ degrés de liberté décrits à l'instant $t$ par :

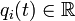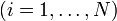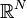les $N$ coordonnées généralisées $q_i(t) \in \mathbb{R}$ , $(i = 1, \dots, N)$ . On peut voir ces coordonnées comme les composantes d'un vecteur de $\mathbb{R}^N$ .

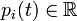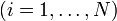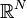les $N$ moments conjugués $p_i(t)\in \mathbb{R}$ , $(i = 1, \dots, N)$ . On peut également voir ces coordonnées comme les composantes d'un autre vecteur de $\mathbb{R}^N$ .

À chaque instant, les $2 N$ coordonnées $(q i (t), p i (t))$ définissent un point $x (t)$ dans l'espace des phases 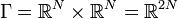$\Gamma = \mathbb{R}^N \times \mathbb{R}^N = \mathbb{R}^{2N}$ à 2N dimensions.

Dynamique sur une variété différentiable

Considérons un système à $N$ degrés de liberté dont les $N$ coordonnées généralisées $q i (t)$ précisent la position d'un point $p$ sur une variété différentielle $M$ à N dimensions.. Le moment conjugué $p j (t)$ est alors un élément de l'espace cotangent 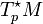$T_p^{\star}M$ dans la direction j.

A chaque instant, les $2 N$ coordonnées $(q i (t), p j (t))$ définissent dans ce cas un point $x (t)$ dans l'espace des phases 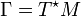$\Gamma = T^{\star}M$ qui s'identifie à l'espace fibré cotangent à 2N dimensions. Cet espace des phases est naturellement muni de la forme symplectique 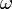$\omega\,$ définie par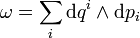
$\omega = \sum_i {\rm d}q^i\wedge{\rm d}p_i \,$
Flot hamiltonien

L'évolution dynamique du système selon les équations canoniques de Hamilton à partir d'une condition initiale 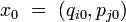$x_0 \ = \ (q_{i0},p_{j0})$ engendre le flot hamiltonien 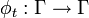$\phi_t : \Gamma \to \Gamma$ , c’est-à-dire le groupe continu à un paramètre tel que :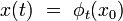

$x(t) \ = \ \phi_t(x_0)$

La succession des positions $x (t)$ dans l'espace des phases se traduit par une courbe continue, appelée orbite.

Théorème de Liouville

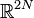Le flot hamiltonien préserve la mesure de Liouville sur l'espace des phases. Lorsque celui-ci est euclidien, cette mesure invariante sous le flot est simplement la mesure de Lebesgue sur $\mathbb{R}^{2N}$ :

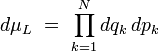
$d\mu_L \ = \ \prod_{k=1}^N dq_k \, dp_k$

La démonstration de ce théorème repose sur le fait que la divergence de la « vitesse » dans l'espace des phases est nulle :

$\mathrm{div} \ \vec{v} \ = \ \sum_{k=1}^N \left[ \ \frac{\partial \dot{q}_k}{\partial q_k} \ + \ \frac{\partial \dot{p}_k}{\partial p_k} \ \right] \ = \ 0$

où on a utilisé les équations canoniques pour conclure. Autrement dit, le « fluide hamiltonien » dans l'espace des phases est incompressible.

Hypersurface d'énergie constante

Un système hamiltonien invariant par translation dans le temps satisfait toujours à la conservation de l'énergie :

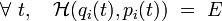
$\forall \ t, \quad \mathcal{H}(q_i(t),p_i(t)) \ = \ E$

de telle sorte que sa dynamique est en fait toujours restreinte à une hypersurface 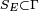$\scriptstyle S_E \subset \Gamma$ à $2 N - 1$ dimensions. Dans ce cas, la mesure de Liouville invariante sous le flot dans l'espace des phases induit une mesure invariante sous le flot sur l'hypersurface d'énergie constante, définie par :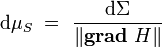

$\mathrm d\mu_S \ = \ \frac{\mathrm d \Sigma}{\| \mathbf{grad} \ H \|}$

où $dΣ$ est la mesure sur l'hypersurface S induite par la métrique sur l'espace des phases.

Système intégrable

Il peut exister d'autres constantes du mouvement indépendantes de l'énergie en plus de celle-ci. Lorsqu'un système invariant par translation défini sur 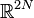${\mathbb R}^{2N}$ dans le temps possède N constantes du mouvement indépendantes, on dit qu'il est intégrable. Sa dynamique est alors particulièrement simple.

Articles connexes

Mécanique classique

Crochet de Poisson

Transformation canonique

Géométrie symplectique

Théorie de Hamilton-Jacobi

Théorème de Noether

Système intégrable

Théorie des perturbations

Mécanique céleste

Problème à N corps

Hypothèse ergodique

Théorème KAM

Théorie du chaos

Physique statistique

Bibliographie

Lev Landau et Evguéni Lifchitz, Physique théorique, tome 1 : Mécanique, éd. MIR, Moscou [détail des éditions]

T. W. B. Kibble et F.H. Berkshire ; Classical Mechanics, Prentice Hall (4^e édition-1997), ISBN 058225972X. Un remarquable cours d'introduction à la mécanique, des fondements newtoniens jusqu'au formalismes plus avancés de Lagrange et de Hamilton. Kibble est professeur émérite de physique théorique de l'Imperial College de Londres. Pour cette 4^e édition (avec un co-auteur), deux chapitres d'introduction aux idées de la théorie du chaos ont été inclus. Niveau : à partir du premier cycle universitaire. (Il a existé une traduction française de l'édition précédente, publiée par Dunod.)

Herbert Goldstein, Charles P. Poole et John L. Safko ; Classical mechanics, Addison-Wesley (3^e édition-2001). Cet ouvrage est une référence concernant les aspects théoriques modernes de la mécanique - formulations lagrangienne et hamiltonienne. Cette troisième édition, réalisée en collaboration, est complétée par un chapitre sur les développements récents de la théorie du chaos. Le chapitre 3, consacré au problème à trois corps, a été également partiellement remanié. Niveau second cycle universitaire. (Il a existé autrefois une traduction française d'une édition précédente.)

Vladimir I. Arnold ; Mathematical methods of classical mechanics, Springer-Verlag (2^e édition-1989). Les aspects mathématiques (principalement géométriques) de la théorie, dans ses formulations modernes - lagrangienne et hamiltonienne -, par un mathématicien russe de premier plan, qui enseigne au XXI^e siècle à l'Université de Paris-Dauphine. Niveau : second cycle universitaire.

R. Abraham et J.E. Marsden ; Foundations of mechanics, the Benjamin/Cummings Publishing Company (2^e édition-1978). Un livre qui présente un exposé axiomatique rigoureux de la mécanique « à la Bourbaki ». Niveau second cycle universitaire minimum.

Walter Thirring ; Classical mathematical physics - Dynamical systems & Field theory, Springer-Verlag (3^e édition-1997), ISBN . La première moitié de ce livre est une présentation rigoureuse de la mécanique, par un physicien mathématicien de l'Université de Vienne. Niveau : second cycle universitaire.

Portail de la physique

Portail des mathématiques

Ce document provient de « M%C3%A9canique hamiltonienne ».

Catégories : Mécanique classique | Méthode mathématique de la physique | Équation différentielle | Physique théorique | Géométrie symplectique

Contenu soumis à la licence CC-BY-SA. Source : Article ℋ de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts